
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Высшая математика. Введение В математический анализ. Учебное пособиеСодержание книги
Поиск на нашем сайте
Ф.В.Чумаков В Ы С Ш А Я М А Т Е М А Т И К А Гл. 6. Введение в математический анализ Учебное пособие
Минск 2003
Высшая математика. Гл.6. Введение в математический анализ. Учебное пособие. Автор Чумаков Ф.В.;Институт парламентаризма и предпринимательства.—Минск.- 71 стр.. Печатается по решению научно –методического Совета И П П (протокол № 3 от 16.10. 2002 г.)
Рецензенты: кафедра теории функций Белорусского государственного университета (зав. кафедрой доктор физико-математических наук, профессор А. А. Килбас), Лазакович Н.В., доктор физико-математических наук, профессор кафедры функционального анализа Белорусского государственного университета.
Содержание
Введение………………………………………………………………….5 §6.1.Множества…………………………………………………….…………6 §6.2.Операции над множествами………………………………………….13 §6.3.Модуль числа…………………………………………………………..16 §6.4.Границы числовых множеств.……………………………………...21 §6.5. Открытые и замкнутые множества ………………………..…..…..29 §6.6.Первоначальные сведения о функциях ……………………….…..42 §6.7.Обратная функция………………………………………………..…...44
§6.8.Сложная функция………………………………………………….….50 §6.9.Элементарные функции………………………. ………………..… 53
§6.10.Метод математической индукции………………………………....63 Литература ………………………………………………...71
Основные символы
В в е д е н и е.
Множество и функция являются основными понятиями, без свободного владения которыми невозможно серьезное изучение математического анализа и других разделов высшей математики. Разъяснение этих понятий проводится на типовых примерах, для решения которых студент должен, как правило, повторить материал школьной математики, восстановить и закрепить навыки, приобретенные в школе. Пособие состоит из десяти параграфов,содержание которых тесно связано с понятиями множества и функции. В конце каждого параграфа приводится перечень вопросов для самостоятельного контроля степени усвоения материала и упражнения для самостоятельной работы.
Первые два параграфа посвящены множествам – фундаменту, на котором строится здание математики. Для более детального изучения числовых множеств вводится понятие модуля и изучаются его свойства (§6.3). В §6.4 изучаются границы числовых множеств, формулируется теорема о существовании точных границ, которая применяется, например, при строгом доказательстве существования предела монотонной ограниченной последовательности. Открытые и замкнутые множества, рассмотренные в §6.5, играют важную роль при изучении свойств непрерывных функций. Понятие функции является центральным, ему посвящен §6.6. В §6.7 дается понятие обратной функции, которое, как правило, довольно сложно для усвоения,поэтому оно разъясняется на простых примерах, причем главное внимание уделяется условиям существования обратной функции. Понятие сложной функции изучается в §6.8. Элементарные функции, на базе которых строится математический анализ, изучаются в §6.9. Приводятся простейшие элементарные функции и описываются их свойства. С методом математической индукции можно ознакомиться §6.10. После усвоения этого понятия становятся простыми и понятными многие важные математические доказательства из теории рядов. Пособие адресовано,в первую очередь, студентам.Однако,оно,на наш взгляд, будет полезным и преподавателям.Его можно применять и как учебник,и как сборник задач с методикой их решения.
.«В самой математике главные средства достигнуть истины-индукция и аналогия». Лаплас. «…наиболее изящные новые истины возникают с помощью индукции». Гаусс. «… математические методы становятся…общими методами для всей науки в целом».Соболев С.Л.
Господь Бог создал целое число, все остальное – дело рук человека. Л. Кронекер [1] Множества.
Совокупность объектов произвольной природы называется множеством. Объекты, из которых состоит множество, называются элементами множства. Так, студент, звезда, кинозал образуют множество и являются элементами этого множества. Множества обозначаются большими буквами латинского алфавита А, В, С, X, Y,..., а их элементы - малыми буквами a, b, c, x, y, … Открытые полупрямые (- ¥, a) = { x | x Î R, - ¥ < x < a }, (a,+ ¥) = { x | x Î R, a < x <+ ¥ }. 6. Числовая прямая (- ¥,+ ¥)=R. Множество может содержать как конечное число элементов, так и бесконечное. В первом случае множество называется конечным, во втором случае бесконечным. Так, множество государств на Земле конечно, а множество натуральных чисел N бесконечно.. Между двумя множествами установлено взаимно однозначное соответствие, если каждому элементу одного из этих множеств поставлен в соответствие единственный элемент другого множества, и наоборот. Из этого следует, что двум различным элементам одного из этих множеств соответствуют два различных элемента другого множества. Так, между натуральными числами и четными натуральными числами можно установить взаимно однозначное соответствие, ставя натуральному числу n в соответствие четное число 2 n, и наоборот.
Два множества называются эквивалентными, если между ними можно установить взаимно однозначное соответствие. Так множества N и
Множество называется счетным, если оно эквивалентно множеству натуральных чисел.
Другими словами, множество счетно, если все его элементы можно пронумеровать. Так, множество всех целых чисел счетно (ниже числовой оси изображены целые числа, а сверху их номера)
Вопросы и задания для самопроверки. Упражнения. 1. Доказать, что число Решение. Предположим противное, т.е., что число + 2. Доказать иррациональность чисел:
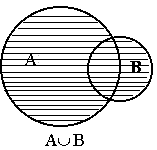
Сравните числа: 1) 4) Операции над множествами. Введем операции над множествами и дадим наглядную иллюстрацию их с помощью кругов Эйлера, точки которых схематически изображают элементы множеств. Пусть А и В некоторые множества. Множество А È В, состоящее из элементов, принадлежащих множеству А или множеству В, или принадлежащих множествам А и В одновременно, называется объединением множеств А и В Очевидно, А È Æ =А, А È А=А; если А Ì В, то А È В=В. Операция объединения множеств распространяется на любое число множеств. Объединением любого числа множеств считается множество, состоящее из элементов, принадлежащих хотя бы одному из заданных множеств.
Вопросы для самопроверки. Упражнения. 1. Доказать, что А È (В Ç С)=(А È В) Ç (А È С). ешение. Пусть элемент х входит в левую часть равенства. Тогда х Î А или х Î В Ç С. Если х Î А, то х Î А È В и х Î А È С, следовательно, х принадлежит правой части доказываемого равенства. Если же х Î В Ç С, то х Î В и х Î С. Но тогда х Î А È В и х Î А È С. Значит, и в этом случае х является элементом правой части. Обратно, пусть теперь х есть элемент правой части. Значит х Î А È В и х Î А È С. Если х Î А, то х Î А È (В Ç С). Если же х не принадлежит А, то х Î В и х Î С. Значит, х Î В Ç С, и опять х принадлежит левой части.
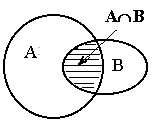
На левом рисунке множество А È В заштриховано горизонтальной штриховкой, а множество А È С - вертикальной штриховкой. Множество (А È В) Ç (А È С) изображено квадратной штриховкой. На правом рисунке множество В Ç С изображено горизонтальной штриховкой, а множество А - вертикальной штриховкой. Заштрихованная область дает множество А È (В Ç С). Мы получили геометрическое доказательство, так как множество, заштрихованное на левом рисунке квадратной штриховкой, и множество, заштрихованное на правом рисунке, совпадают. 2. Доказать, что А È В=В È А (свойство коммутативности объединения множеств). 3. А Ç В=В Ç А (свойство коммутативности пересечения множеств). Доказать. 4. (А È В) È С=А È (В È С) (свойство ассоциативности объединения множеств). Доказать 5. Доказать, что (А Ç В) Ç С=А Ç (В Ç С)= А Ç В Ç С (свойство ассоциативности пересечения множеств). 6. Убедиться, что три соотношения А Ì В, А Ç В=А, А È В=В равносильны, то есть, что из выполнения любого из них вытекает справедливость остальных двух. 7. Верно ли равенство А Ç В=А\(A\B)? 8. (A\B)\C=A\(B È C). Доказать. 9. Верно ли соотношение (A\B) Ç (C\D)=(A Ç C)\(B Ç D)? 10. Доказать, что условие (A È B)\B=A выполняется в том и только том случае, когда A Ç B= Æ. 11. (A\B) È B=A Û B Ì A. Доказать. 12. Доказать, что операции È и Ç связаны законами дистрибутивности: (A È B) Ç C=(A Ç C) È (B Ç C), (A Ç B) È C=(A È C) Ç (B È C), 13. Если A Ì B, то A È B=B? 14. A È Æ =A? 15. Если A Ì B, A Ç B=A? 16. Доказать, что A=B, если A Ì B и B Ì A. 17. Если A Ì B и B Ì C, то A Ì C. Доказать. 18. Следует ли из A Ç B=A соотношение A Ì B? 19. Вытекает ли из A\B=С, что А=B È C? 20. Вытекает ли из A=B È C, что A\B=C? 21. Верно ли, что A\(B È C)=(A\B)\C? 22. A È (B\C)=(A È B)\C? 23. (A\B) È C=(A È C)\B? Н. Винер Модуль числа. Модулем (абсолютной величиной) действительного числа х называется само число х, если х ³ 0, и противоположное число -х, если х < 0. Модуль числа х обозначается | х |. Согласно определению
Например, |3|=3, |0|=0, |-5|=-(-5)=5. Доказательства свойств 1-6 вытекают непосредственно из определения модуля. Докажем свойства 7 и 8. На основании свойства 2 для любых чисел х и у имеем -|x| £ х £ |x|, -|y| £ y £ |y|. Складывая эти неравенства, находим, что (|x+y|) £ х+у £ |x| + |y|. По свойству 3 получаем неравенство 7. Пусть теперь х=(х-у)+у. Тогда |x|=|(x-y)+y| £ |х-у|+y по формуле 7, то есть |x-y| ³ |x|-|y|. C другой стороны |y|=|(y-x)+x|. По формуле 7 имеем |y| £ |y-х|+x. Отсюда |x|-|y| ³ |y-x|. Значит,||x|-|y|| £ |x-y|. Заметим, что величина |x-y| есть расстояние на числовой оси между точками М и Т с координатами х и у соответственно (независимо от их расположения). М(х) |x-y| T(y)
x y 0 Из определения модуля вытекает, что Вопросы для самопроверки. Упражнения. 1.Решить неравенство Решение. Прежде всего находим точки, в которых обращаются в нуль выражения под знаком модуля: Решить уравнения: 1) 4) 7) 10) 13). 16) 19). 3. Решить неравенства и изобразить решения на числовой оси: 1) 5) 9) 4. Изобразить на координатной плоскости множества точек, координаты которых удовлетворяют следующим соотношениям: 1) 5) 9) 13) 16) 19) 22) 22) Ни одно человеческое исследование не может называться истинной наукой,если оно не прошло через Границы числовых множеств. Пусть Х – некоторое непустое числовое множество. Множество Х называется ограниченным сверху, если существует такое число М, что каждое число х из множества Х не превосходит числа М, т.е.
В этом случае Множество Х называется ограниченным, если оно ограничено и сверху и снизу, т.е. если существуют такие числа m и М, что каждое число х из множества Х удовлетворяяет неравенству
Например, множество Х=(0, 1] ограничено и сверху и снизу. Сверху оно ограничено любым числом Ограниченность множества Х равносильна существованию такого положительного числа С, что каждый элемент множества Х удовлетворяет неравенству В самом деле, если множество Х ограничено, то существуют такие числа m и M, что каждое число х из множества Х удовлетворяет неравенству
Всякое ограниченное сверху (снизу) множество имеет бесконечно много верхних (нижних) границ, а ограниченное множество имеет бесконечно много и верхних, и нижних границ одновременно. В самом деле, если М есть верхняя грань множества,то и всякое число М+произвольное положительное число также является верхней гранью(?), если же m есть нижняя грань множества,то и всякое число m- произвольное положительное число также является нижней гранью(?). Наименьшая из всех верхних границ ограниченного сверху множества Х называется точной верхней границей (гранью) множества Х и обозначается supX (sup – первые буквы латинского слова supremum – верхний); наибольшая из всех нижних границ ограниченного снизу множества Х называется точной нижней границей (гранью) множества Х и обозначается inf X (inf– первые буквы латинского слова infimum – нижний ). Возникает вопрос: всякое ли ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) границу? Ответ на эти вопросы дает следующая Теорема (о существовании точных границ). Всякое непустое ограниченное сверху (снизу) множество Х имеет (единственную!) точную верхнюю границу
Из теоремы следует, что всякое ограниченное множество имеет одну точную верхнюю и одну точную нижнюю границы. Например, Отметим важнейшие свойства точных границ числовых множеств. Пусть 1. 2. 3. если m – какая-либо нижняя граница множества Х, то Пусть. Тогда: 4. 5. 6. если М – какая-либо верхняя граница множества Х, то Упражнения.
1. Найдите наибольший и наименьший элементы множества 2. Имеет ли множество 3. Ограничено ли множество 4. Имеет ли множество рациональных чисел в промежутке [0, 1) наименьший элемент?, наибольший элемент? Является ли 5. Ограничено ли множество 6. Ограничено ли множество 7. Найдите точные границы множества 8. Укажите точные границы множества 9. Пусть Х – множество всех рациональных чисел, удовлетворяющих неравенству Решение. Неравенство 10. Найти sup X, inf X, если Х-множество рациональных ч
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.29.255 (0.015 с.) |

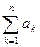 есть краткая запись суммы
есть краткая запись суммы 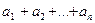
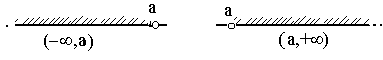
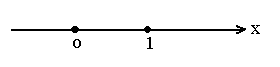
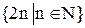 являются эквивалентными.
являются эквивалентными.
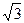 +
+ 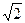 является иррациональным числом.
является иррациональным числом.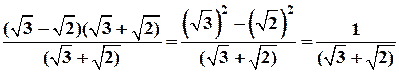 будет также рациональным, как частное двух рациональных чисел 1 и
будет также рациональным, как частное двух рациональных чисел 1 и 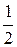 (
(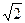 . Значит, наше предположение ложно, и число
. Значит, наше предположение ложно, и число 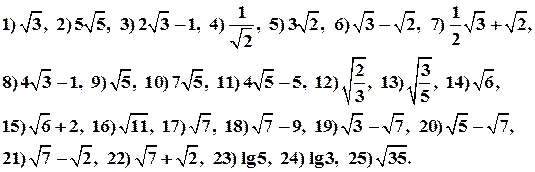
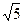 и
и 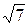 - 2, 3)
- 2, 3) 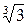 - 1 и
- 1 и 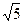 - 2,
- 2,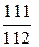 и
и 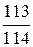 , 6)
, 6) 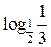 и
и 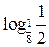 , 7)
, 7) 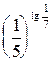 и
и 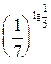 .
.
 Пусть А={x Î R ½ x2-5x+6=0}, В={x Î R ½
Пусть А={x Î R ½ x2-5x+6=0}, В={x Î R ½ 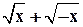 ÎR},
ÎR},  }. Очевидно, что А={2,3}, В={0}, С= Æ. Поэтому А È В È С={0,2,3}.
}. Очевидно, что А={2,3}, В={0}, С= Æ. Поэтому А È В È С={0,2,3}.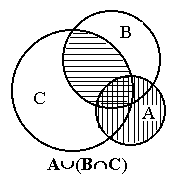
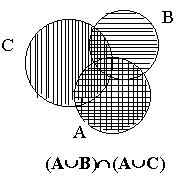
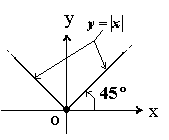
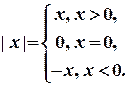 (6.1)
(6.1)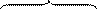
 · · ·
· · ·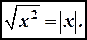 (6.2)
(6.2)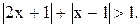
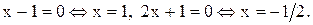 Точками
Точками  и
и 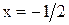 делим числовую прямую на три промежутка:
делим числовую прямую на три промежутка: 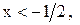
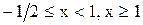 и рассматриваем исходное неравенство на каждом промежутке в отдельности. На первом промежутке (
и рассматриваем исходное неравенство на каждом промежутке в отдельности. На первом промежутке (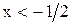 ) неравенство принимает вид
) неравенство принимает вид  так как
так как 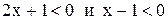 для
для 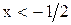 и, значит,
и, значит, 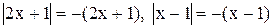 по определению модуля. Не все найденные нами решения (
по определению модуля. Не все найденные нами решения (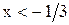 ) попадают в промежуток
) попадают в промежуток 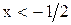 , для указанных промежутков (
, для указанных промежутков (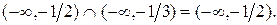 Следовательно, весь промежуток
Следовательно, весь промежуток 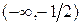 является решением исходного неравенства. Если же
является решением исходного неравенства. Если же 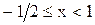 , то
, то 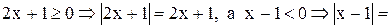
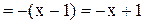 . Неравенство в этом случае примет вид:
. Неравенство в этом случае примет вид: 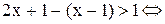
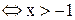 . Все точки промежутка
. Все точки промежутка 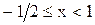 удовлетворяют неравенству
удовлетворяют неравенству 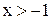 и, следовательно, являются решением исходного неравенства. На третьем промежутке (
и, следовательно, являются решением исходного неравенства. На третьем промежутке (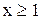 ) исходное неравенство равносильно системе
) исходное неравенство равносильно системе 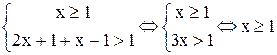 . Объединяя все найденные решения, получим решение исходного неравенства:
. Объединяя все найденные решения, получим решение исходного неравенства: 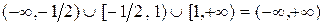 . Аналогично рассматриваются уравнения, содержащие неизвестную величину под знаком модуля.
. Аналогично рассматриваются уравнения, содержащие неизвестную величину под знаком модуля.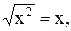 2)
2)  3)
3) 
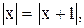 5)
5) 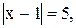 6)
6) 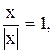
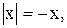 8)
8) 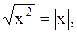 9)
9) 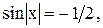
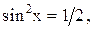 11)
11) 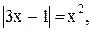 12)
12) 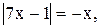
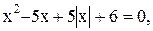 14)
14) 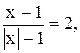 15)
15) 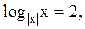
 17)
17) 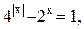 18)
18) 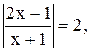
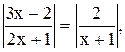 20)
20) 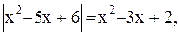 21)
21) 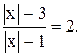
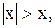 2)
2) 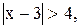 3)
3) 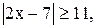 4)
4) 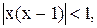
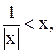 6)
6) 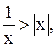 7)
7)  8)
8) 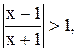
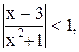 10)
10) 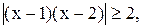 11)
11) 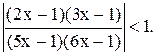
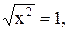 2)
2) 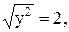 3)
3) 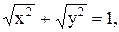 4)
4) 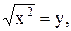
 6)
6) 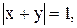 7)
7) 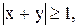 8)
8) 
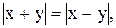 10)
10) 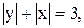 11)
11) 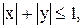 12)
12) 
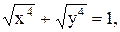 14)
14)  15)
15) 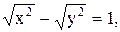
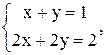 17)
17) 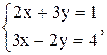 18)
18) 
 20)
20) 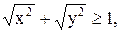 21)
21) 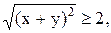
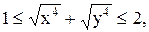 23)
23) 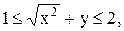 24)
24) 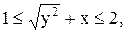
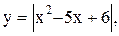 26
26 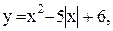 28)
28) 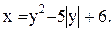
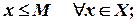 число М называется верхней границей (или гранью) множества Х.
число М называется верхней границей (или гранью) множества Х.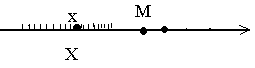 В этом случае все точки х из множества Х расположены слева от точки М. Так, множество Х={-1, -2, -3, -4,...} ограничено сверху любым числом
В этом случае все точки х из множества Х расположены слева от точки М. Так, множество Х={-1, -2, -3, -4,...} ограничено сверху любым числом 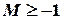 . Каждое такое число является верхней границей данного множества. Множество N ={1, 2, 3,...} не будет ограниченным сверху, так как для любого числа М, каким бы большим оно ни было, найдется целое положительное число из множества N большее М.
. Каждое такое число является верхней границей данного множества. Множество N ={1, 2, 3,...} не будет ограниченным сверху, так как для любого числа М, каким бы большим оно ни было, найдется целое положительное число из множества N большее М.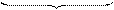
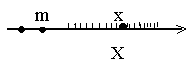 Множество Х называется ограниченным снизу, если существует такое число m, что каждое число х из множества Х не меньше числа m, т.е.
Множество Х называется ограниченным снизу, если существует такое число m, что каждое число х из множества Х не меньше числа m, т.е. 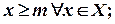 число m называется нижней границей (или гранью) множества Х.
число m называется нижней границей (или гранью) множества Х.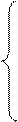
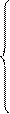 в се точки х из множества Х расположены справа от точки m. Например, множество N ={1, 2, 3,... } ограничено снизу любым числом
в се точки х из множества Х расположены справа от точки m. Например, множество N ={1, 2, 3,... } ограничено снизу любым числом 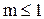 . Каждое такое число является нижней границей данного множества. Множество Х={-1, -2, -3, -4,...} не будет ограниченным снизу, так как для любого числа m, каким бы большим оно ни было, найдется целое отрицательное число из Х меньшее m.
. Каждое такое число является нижней границей данного множества. Множество Х={-1, -2, -3, -4,...} не будет ограниченным снизу, так как для любого числа m, каким бы большим оно ни было, найдется целое отрицательное число из Х меньшее m.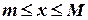 .
.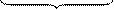
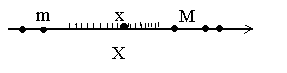
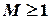 , а снизу – любым числом
, а снизу – любым числом 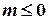 . Множество Z ={..., -1, 0, 1, 2,...} не является ограниченым ни снизу, ни сверху (почему?). Условимся считать пустое множество Æ ограниченным.
. Множество Z ={..., -1, 0, 1, 2,...} не является ограниченым ни снизу, ни сверху (почему?). Условимся считать пустое множество Æ ограниченным.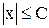 .
.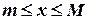 . Пусть С есть наибольшее из чисел
. Пусть С есть наибольшее из чисел 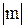 и
и 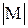 . Тогда, очевидно,, т.е.
. Тогда, очевидно,, т.е. 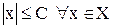 . И наоборот, если для любого
. И наоборот, если для любого 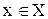 верно неравенство
верно неравенство 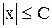 , то
, то 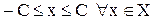 , т.е. множество Х ограничено (числом
, т.е. множество Х ограничено (числом 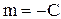 снизу и числом
снизу и числом 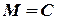 сверху).
сверху).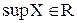 (точную нижнюю границу
(точную нижнюю границу 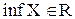 ).
).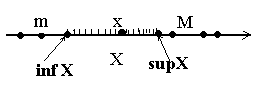
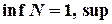
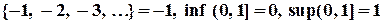 .
.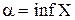 . Тогда:
. Тогда: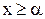 для каждого
для каждого 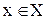 , ибо
, ибо 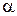 есть нижняя граница множества Х;
есть нижняя граница множества Х;
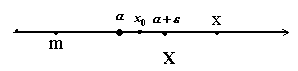 для любого
для любого 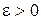 всегда найдется элемент
всегда найдется элемент  из Х такой, что
из Х такой, что 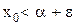 (в противном случае
(в противном случае 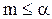 , ибо
, ибо 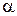 – наибольшая из всех нижних границ Х.
– наибольшая из всех нижних границ Х.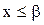 для каждого х из Х, ибо
для каждого х из Х, ибо 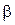 есть верхняя граница множества Х;
есть верхняя граница множества Х;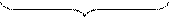
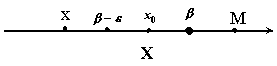 для любого
для любого 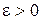 всегда существует элемент
всегда существует элемент 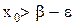 (в противном случае
(в противном случае 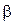 не было бы точной верхней границей множества Х, почему?);
не было бы точной верхней границей множества Х, почему?);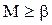 , ибо
, ибо  – наименьшая из всех верхних граней множества Х.
– наименьшая из всех верхних граней множества Х.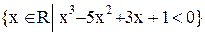 .Является ли число 5 верхней границей множества
.Является ли число 5 верхней границей множества 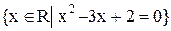 ?
?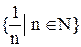 наименьший элемент?, наибольший элемент? Найдите точные границы этого множества.
наименьший элемент?, наибольший элемент? Найдите точные границы этого множества.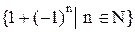 ? Найдите точные границы этого множества.
? Найдите точные границы этого множества.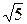 верхней границей множества рациональных чисел в промежутке [0, 1)?
верхней границей множества рациональных чисел в промежутке [0, 1)?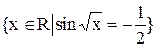 ?
?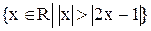 ?
? .
.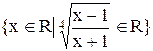 .
.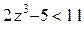 . Найти sup X, inf X.
. Найти sup X, inf X.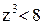 . Извлекая корень, получим, что
. Извлекая корень, получим, что 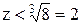 . Очевидно, наименьшей из верхних границ будет число 2, т.е.
. Очевидно, наименьшей из верхних границ будет число 2, т.е. 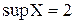 . Так как множество Х неограничено снизу, то
. Так как множество Х неограничено снизу, то  .
.


