
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрические и обратные тригонометрические функции.Содержание книги
Поиск на нашем сайте
1о
Сужение функции 2о Основные значения
Сужение функции
Основные значения фунуции у=
Сужение функции
Основные значения функции у=
Сужение функции 8).
. Основные значения функции у=
Основные тригонометрические формулы. Формулы сложения
Из предыдущих формул находим:
Полагая ,. Далее: Из формулы для Полагая в формулах сложения Элементарной функцией называется каждая функция, которая получена из основных элементарных функций при помощи конечного числа операций сложения, вычитания, умножения, деления и композиции функций. Так, элементарными функциями являются гиперболические функции:
Формулы являются основными для гиперболических функций и напоминают соответствующие формулы для тригонометрических функций. Множество всех элементарных функций состоит из алгебраических и трансцендентных функций. Каждая функция где
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.107.144 (0.007 с.) |

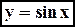 ,
, 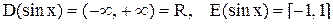 . Данная функция является нечетной, т.к.
. Данная функция является нечетной, т.к. 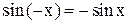 , и периодической с периодом
, и периодической с периодом  . (Рис. 41)
. (Рис. 41) на отрезок
на отрезок 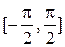 (график сужения изображен утолщенной линией на рис.41) является строго возрастающей функцией и, следовательно, имеет обратную функцию.
(график сужения изображен утолщенной линией на рис.41) является строго возрастающей функцией и, следовательно, имеет обратную функцию. ,
, 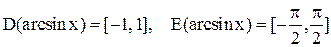 . График функции
. График функции 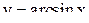 получается зеркальным отображением утолщенной части синусоиды относительно прямой
получается зеркальным отображением утолщенной части синусоиды относительно прямой  (рис. 42). Из определения обратной функции следует, что
(рис. 42). Из определения обратной функции следует, что  . Так как
. Так как  , то функция
, то функция  является нечетной.
является нечетной.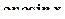





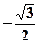


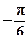

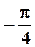
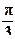


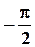
 3).
3). 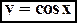 ,
,  . Данная функция является четной, т.к.
. Данная функция является четной, т.к. 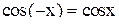 , и периодической с периодом
, и периодической с периодом  на отрезок
на отрезок 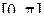 (график сужения изображен утолщенной линией) является строго убывающей функцией и, следовательно, имеет обратную функцию.
(график сужения изображен утолщенной линией) является строго убывающей функцией и, следовательно, имеет обратную функцию. 4).
4). 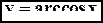 ,
,  . График функции
. График функции 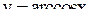 получается зеркальным отображением утолщенной части косинусоиды относительно прямой
получается зеркальным отображением утолщенной части косинусоиды относительно прямой  . Из определения обратной функции следует, что
. Из определения обратной функции следует, что 
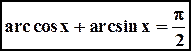 .
.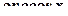 :
:

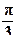
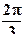
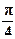
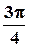
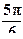
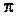
 5).
5). 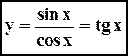 ,
,  . Д анная функция является нечетной и периодической с периодом
. Д анная функция является нечетной и периодической с периодом  .
.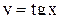 на интервал
на интервал 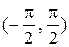 является строго возрастающей функцией и, следовательно, имеет обратную функцию.
является строго возрастающей функцией и, следовательно, имеет обратную функцию. 6).
6). 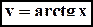 , для которой
, для которой 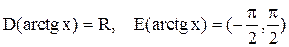 . Так как
. Так как  , то функция
, то функция 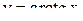 является нечетной. Из определения обратной функции следует, что
является нечетной. Из определения обратной функции следует, что  .
.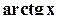 :
: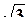

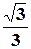


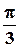
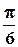

 7).
7). 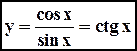 ,
,  . Данная функция является нечетной и периодической с периодом
. Данная функция является нечетной и периодической с периодом 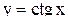 на интервал
на интервал 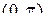 является строго убывающей функцией и, следовательно, имеет обратную функцию.
является строго убывающей функцией и, следовательно, имеет обратную функцию. , для которой
, для которой 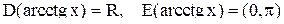 Из определения обратной функции следует, что
Из определения обратной функции следует, что 

 .
.  :
:
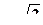



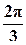
 ,
,  .
. ,
, 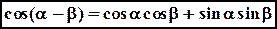 .
.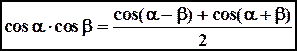 ,
,  .
.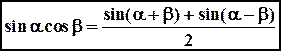 .
. , находим:
, находим:
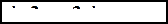 ..
.. . Таким образом,
. Таким образом,  – формула сложения для тангенса, откуда при
– формула сложения для тангенса, откуда при 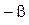 получаем:
получаем:  .
. при
при 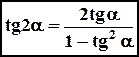 .
.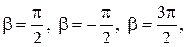
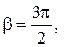
 , мы получим формулы приведения для тригонометрических функций. Так, в частности,
, мы получим формулы приведения для тригонометрических функций. Так, в частности, 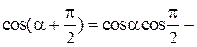
 . Аналогично,
. Аналогично,  и т.д..
и т.д..

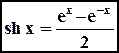 (гиперболический синус),
(гиперболический синус),  (гиперболический косинус),
(гиперболический косинус),  =
=  (гиперболический тангенс),
(гиперболический тангенс), 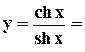
 (гиперболический котангенс). Графики этих функций имеют вид:
(гиперболический котангенс). Графики этих функций имеют вид: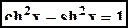 ,
, 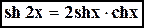 ,
, 
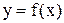 , удовлетворяющая при некотором
, удовлетворяющая при некотором  N уравнению
N уравнению ,
, – многочлены относительно переменной х, называется алгебраической.
– многочлены относительно переменной х, называется алгебраической.


