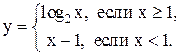В.П. Ермаков
Обратная функция.

 Предположим, что функция
Предположим, что функция 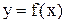 определена на отрезке [a, b], причем значения, принимаемые данной функцией в разных точках отрезка [a, b] сплошь заполняют некоторый отрезок [c, d]. Из определения функции вытекает, что для каждого значения х0 аргумента х из отрезка [a, b] есть только одно значение у0 функции у из отрезка [c, d], такое, что
определена на отрезке [a, b], причем значения, принимаемые данной функцией в разных точках отрезка [a, b] сплошь заполняют некоторый отрезок [c, d]. Из определения функции вытекает, что для каждого значения х0 аргумента х из отрезка [a, b] есть только одно значение у0 функции у из отрезка [c, d], такое, что 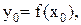 т.е. любая прямая параллельная оси ОУ, пересекающая ось ОХ между точками a и b, пересекает график функции
т.е. любая прямая параллельная оси ОУ, пересекающая ось ОХ между точками a и b, пересекает график функции 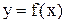 лишь в одной точке. Обратное, вообще говоря, неверно. Так, функция, график которой изображен на рисунке справа в трех точках
лишь в одной точке. Обратное, вообще говоря, неверно. Так, функция, график которой изображен на рисунке справа в трех точках  отрезка [a, b] принимает одно и то же значение
отрезка [a, b] принимает одно и то же значение 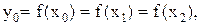 т.е. значению функции
т.е. значению функции 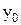 соответствуют три различные точки
соответствуют три различные точки 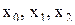 отрезка [a, b], в которых значения функции
отрезка [a, b], в которых значения функции 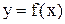 совпадают.Однако, если функция
совпадают.Однако, если функция 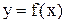 является строго возрастающей (функция, график которой изображен выше таковой не является!), то дело обстоит иначе. Рассмотрим строго возрастающую функцию, график которой изображен слева.
является строго возрастающей (функция, график которой изображен выше таковой не является!), то дело обстоит иначе. Рассмотрим строго возрастающую функцию, график которой изображен слева.
На графике данной функции видно, что каждому значению функции 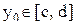 соответствует единственное число
соответствует единственное число  такое, что
такое, что 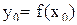 . Докажем данное утверждение методом от противного. Предположим, что для каждого числа
. Докажем данное утверждение методом от противного. Предположим, что для каждого числа 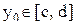 найдутся две точки
найдутся две точки 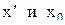 из отрезка [a, b], в которых функция принимает значение
из отрезка [a, b], в которых функция принимает значение  , т.е.
, т.е. 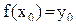 и
и  . Пусть, например,
. Пусть, например,  . Так как функция строго возрастает, тодолжно выполняться неравенство
. Так как функция строго возрастает, тодолжно выполняться неравенство 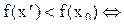
 , что невозможно. Если предположить, что
, что невозможно. Если предположить, что  , то получим
, то получим 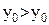 , что также невозможно. Рассуждая аналогично, мы придем к противоречию, если предположить, что числу
, что также невозможно. Рассуждая аналогично, мы придем к противоречию, если предположить, что числу 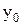 соответствует более двух точек из отрезка [a, b], в которых функция принимает одно и то же значение. Значит, наше предположение ложно, и, следовательно, каждому значению
соответствует более двух точек из отрезка [a, b], в которых функция принимает одно и то же значение. Значит, наше предположение ложно, и, следовательно, каждому значению 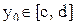 соответствует одно и только одно значение
соответствует одно и только одно значение  такое, что
такое, что 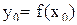 . К такому же выводу придём, если рассматривать строго убывающую функцию. Таким образом, если функция
. К такому же выводу придём, если рассматривать строго убывающую функцию. Таким образом, если функция 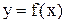 является строго монотонной на промежутке, то существует некоторое правило
является строго монотонной на промежутке, то существует некоторое правило 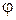 , по которому каждому значению
, по которому каждому значению  ставится в соответствие такое единственное число
ставится в соответствие такое единственное число 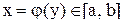 , которое удовлетворяет условию
, которое удовлетворяет условию 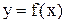 , т.е. переменные х и у удовлетворяют определению функции, причем переменная х играет роль функции, а переменная у – роль аргумента. Функция
, т.е. переменные х и у удовлетворяют определению функции, причем переменная х играет роль функции, а переменная у – роль аргумента. Функция 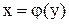 называется обратной по отношению к функции
называется обратной по отношению к функции 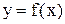 . Правило
. Правило 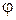 , задающее обратную функцию, обозначают
, задающее обратную функцию, обозначают 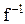 и записывают в виде
и записывают в виде 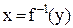 . Очевидно, графики функций
. Очевидно, графики функций 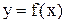 и обратной к ней функции
и обратной к ней функции 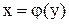 совпадают. Действительно, если точка (х, у) «лежит» на графике функции
совпадают. Действительно, если точка (х, у) «лежит» на графике функции  , то ее координаты удовлетворяют условию
, то ее координаты удовлетворяют условию 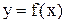 , а, значит, и уравнению
, а, значит, и уравнению 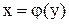 . Для функции, заданной аналитически формулой
. Для функции, заданной аналитически формулой 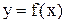 , обратную функцию иногда можно получить, выразив х через у, решив уравнение
, обратную функцию иногда можно получить, выразив х через у, решив уравнение 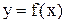 относительно переменной х. Заметим, что обратная функция
относительно переменной х. Заметим, что обратная функция 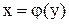 будет строго возрастать (убывать), если функция
будет строго возрастать (убывать), если функция 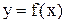 строго возрастает (убывает). Пусть, например, функци
строго возрастает (убывает). Пусть, например, функци 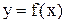 строговозрастает,и
строговозрастает,и 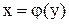 – ее обратная функция (см.рисунок). Если
– ее обратная функция (см.рисунок). Если 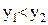 , т.е.
, т.е. 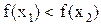 , то
, то 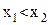 , ибо функция
, ибо функция 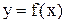 строго возрастает, т.е.
строго возрастает, т.е. 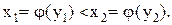 Аналогично рассматривается случай строго убывающей функции. На верхнем рисунке изображен график функции, которая не имеет обратной, хотя бы потому, что значению
Аналогично рассматривается случай строго убывающей функции. На верхнем рисунке изображен график функции, которая не имеет обратной, хотя бы потому, что значению  соответствуют три (а не одно!) значения
соответствуют три (а не одно!) значения 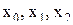 переменной х, при которых функция принимает значение
переменной х, при которых функция принимает значение  . Таким образом,
. Таким образом,
строго монотонная на промежутке функция 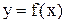 имеет обратную функцию
имеет обратную функцию 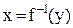 , которая определена на множестве ее значений,причем обратная функция строго возрастает,если функция
, которая определена на множестве ее значений,причем обратная функция строго возрастает,если функция 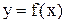 строго возрастает,и строго убывает,если
строго возрастает,и строго убывает,если 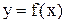 убывает.
убывает.
Следуя традиции обозначать независимую переменную через х, а зависимую – буквой у, обратную функцию  будем записывать в виде
будем записывать в виде 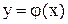 или
или 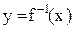 . В этом случае множества, на которых изменяются переменные х и у, меняются местами. Так, если для исходной функции
. В этом случае множества, на которых изменяются переменные х и у, меняются местами. Так, если для исходной функции 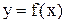 переменная х изменяется на множестве Х, а переменная у – на множестве Y, то для обратной функции
переменная х изменяется на множестве Х, а переменная у – на множестве Y, то для обратной функции 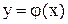 переменная х изменяется на множестве Y, а переменная у – на множестве Х.
переменная х изменяется на множестве Y, а переменная у – на множестве Х.
 Если точка (х, у) принадлежит графику функции
Если точка (х, у) принадлежит графику функции 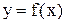 , то точка (у, х) будет принадлежать графику функции
, то точка (у, х) будет принадлежать графику функции 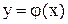 . Из этого следует, что график обратной функции
. Из этого следует, что график обратной функции 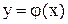 (или
(или 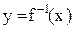 ) может быть получен из графика функции
) может быть получен из графика функции 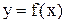 зеркальным отображением (осевой симметрией) относительно прямой
зеркальным отображением (осевой симметрией) относительно прямой  ,потому что зеркальным отражением произвольной точки (a, b) относительно прямой
,потому что зеркальным отражением произвольной точки (a, b) относительно прямой  является точка (b, a).
является точка (b, a).
 Функция
Функция  определена на бесконечном промежутке
определена на бесконечном промежутке 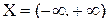 ,
, 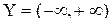 – множество ее значений. Так как данная функция является строго возрастающей на R, то она имеет обратную функцию
– множество ее значений. Так как данная функция является строго возрастающей на R, то она имеет обратную функцию  , которую находим, решая уравнение
, которую находим, решая уравнение  относительно переменнной
относительно переменнной 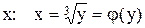 . Меняя х и у местами, получим привычную запись обратной функции в виде
. Меняя х и у местами, получим привычную запись обратной функции в виде 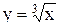 . Ее график симметричен кривой
. Ее график симметричен кривой 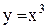 относительно прямой
относительно прямой  и изображен пунктирной линией на рисунке.
и изображен пунктирной линией на рисунке.
 Функция
Функция  определена на бесконечном промежутке
определена на бесконечном промежутке
 , множество ее значений образует бесконечный промежуток
, множество ее значений образует бесконечный промежуток 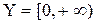 . Так как данная функция не является строго монотонной на Х (почему?), то она не имеет обратной функции.
. Так как данная функция не является строго монотонной на Х (почему?), то она не имеет обратной функции.
 Пусть D(f) – область определения функции
Пусть D(f) – область определения функции 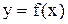 , а Х – подмножество области определения ее D(f). Функция
, а Х – подмножество области определения ее D(f). Функция 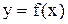 , рассматриваемая на множестве Х, называется сужением функции
, рассматриваемая на множестве Х, называется сужением функции 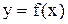 на множество Х. Рассмотрим теперь сужение функции
на множество Х. Рассмотрим теперь сужение функции 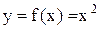 на промежуток
на промежуток 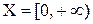 ,
, 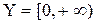 – множество значений сужения f. На множестве
– множество значений сужения f. На множестве 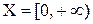 функция
функция 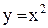 строго возрастает, и, следовательно, имеет обратную функцию. Решая уравнение
строго возрастает, и, следовательно, имеет обратную функцию. Решая уравнение 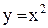 относительно х, находим, что
относительно х, находим, что 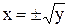 . Так как переменная х принимает неотрицательные значения (
. Так как переменная х принимает неотрицательные значения (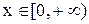 ), то
), то  . Меняя х и у местами, находим, что обратная функция задается формулой
. Меняя х и у местами, находим, что обратная функция задается формулой 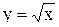 .
.
 Рассматривая сужение функции
Рассматривая сужение функции  на множество
на множество 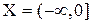 , найдем, что она удовлетворяет условиям существования обратной функции (как строго убывающая функция). Решая уравнение
, найдем, что она удовлетворяет условиям существования обратной функции (как строго убывающая функция). Решая уравнение 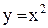 относительно х, находим, что
относительно х, находим, что 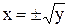 . Так как
. Так как 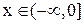 , то
, то  , откуда, находим, что обратная функция задается формулой (см.рисунок).
, откуда, находим, что обратная функция задается формулой (см.рисунок).
Вопросы и задания для самопроверки.
1. Что такое обратная функция? Приведите примеры.
2. Укажите условия, при которых существует обратная функция.
3. Совпадают ли графики функций  ,
,  ?
?
4. Как построить график обратной функции 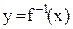 , если известен график функции
, если известен график функции  ?
?
5. Укажите область определения и область изменения обратной функции 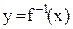 , если исходная функция определена на множестве Х, а Y– множество ее значений?
, если исходная функция определена на множестве Х, а Y– множество ее значений?
6. Может ли не строго монотонная функция иметь обратную функцию?
7. Обязательно ли функция является строго монотонной, если она имеет обратную?
8. Может ли функция 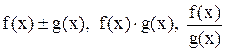 иметь обратную, если функция f(x) имеет обратную, а функция g(x) – не имеет? Приведите примеры.
иметь обратную, если функция f(x) имеет обратную, а функция g(x) – не имеет? Приведите примеры.
9. Может ли функция f(x)+g(x) иметь обратную, если функции f(x) и g(x) не имеют обратной функции? Приведите примеры.
Упражнения.
1. Для функции 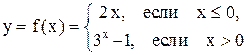 найти обратную функцию, построить график, указать область ее определения.
найти обратную функцию, построить график, указать область ее определения.
 Решение. Так как данная функция строго возрастает на числовой оси, то она имеет обратную функцию. Найдем ее. Если
Решение. Так как данная функция строго возрастает на числовой оси, то она имеет обратную функцию. Найдем ее. Если 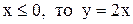 , причем, значения функции образуют бесконечный промежуток
, причем, значения функции образуют бесконечный промежуток 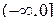 . Очевидно,
. Очевидно, 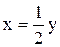 . Значит,
. Значит, 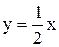 – «часть» обратной функции для
– «часть» обратной функции для 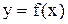 , областью определения которой является множество
, областью определения которой является множество 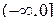 , а множество значений – также промежуток
, а множество значений – также промежуток 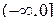 . Таким образом, мы построили «часть» обратной функции. Пусть теперь
. Таким образом, мы построили «часть» обратной функции. Пусть теперь 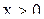 , тогда
, тогда  . Находим из последнего уравнения х:
. Находим из последнего уравнения х: 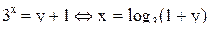 . Следовательно, функция
. Следовательно, функция 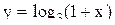 – еще одна «часть» обратной функции (или правильнее сказать еще одно ее сужение), причем,
– еще одна «часть» обратной функции (или правильнее сказать еще одно ее сужение), причем, 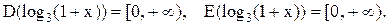 Объединяя полученные формулы в одну, получим обратную к исходной функции:
Объединяя полученные формулы в одну, получим обратную к исходной функции: 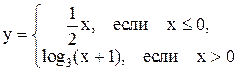 . Ее график изображен на рисунке пунктирной линией.. Он получен путем зеркального отображения исходной функции (симметрии) относительно прямой
. Ее график изображен на рисунке пунктирной линией.. Он получен путем зеркального отображения исходной функции (симметрии) относительно прямой  .
.
2. Для указанных ниже функций найти обратные функции и построить эскизы их графиков:
1.  2.
2. 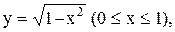 3.
3. 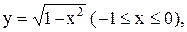
4. 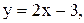 5.
5. 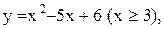 6.
6. 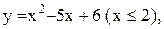
7. 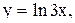 8.
8. 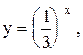 9.
9. 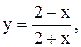
10. 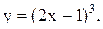 11.
11. 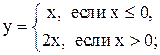 12.
12. 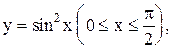
13. 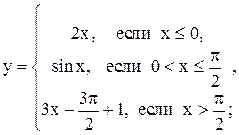 14.
14. 
15. 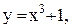 16.
16. 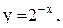 17.
17. 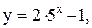
18. 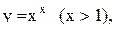 19.
19. 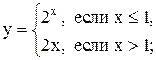 20.
20. 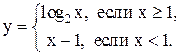



 Предположим, что функция
Предположим, что функция 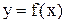 определена на отрезке [a, b], причем значения, принимаемые данной функцией в разных точках отрезка [a, b] сплошь заполняют некоторый отрезок [c, d]. Из определения функции вытекает, что для каждого значения х0 аргумента х из отрезка [a, b] есть только одно значение у0 функции у из отрезка [c, d], такое, что
определена на отрезке [a, b], причем значения, принимаемые данной функцией в разных точках отрезка [a, b] сплошь заполняют некоторый отрезок [c, d]. Из определения функции вытекает, что для каждого значения х0 аргумента х из отрезка [a, b] есть только одно значение у0 функции у из отрезка [c, d], такое, что 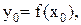 т.е. любая прямая параллельная оси ОУ, пересекающая ось ОХ между точками a и b, пересекает график функции
т.е. любая прямая параллельная оси ОУ, пересекающая ось ОХ между точками a и b, пересекает график функции  отрезка [a, b] принимает одно и то же значение
отрезка [a, b] принимает одно и то же значение 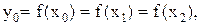 т.е. значению функции
т.е. значению функции 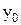 соответствуют три различные точки
соответствуют три различные точки 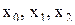 отрезка [a, b], в которых значения функции
отрезка [a, b], в которых значения функции 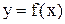 совпадают.Однако, если функция
совпадают.Однако, если функция 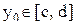 соответствует единственное число
соответствует единственное число  такое, что
такое, что 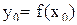 . Докажем данное утверждение методом от противного. Предположим, что для каждого числа
. Докажем данное утверждение методом от противного. Предположим, что для каждого числа 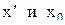 из отрезка [a, b], в которых функция принимает значение
из отрезка [a, b], в которых функция принимает значение  , т.е.
, т.е. 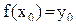 и
и  . Пусть, например,
. Пусть, например,  . Так как функция строго возрастает, тодолжно выполняться неравенство
. Так как функция строго возрастает, тодолжно выполняться неравенство 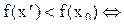
 , что невозможно. Если предположить, что
, что невозможно. Если предположить, что  , то получим
, то получим 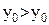 , что также невозможно. Рассуждая аналогично, мы придем к противоречию, если предположить, что числу
, что также невозможно. Рассуждая аналогично, мы придем к противоречию, если предположить, что числу 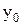 соответствует более двух точек из отрезка [a, b], в которых функция принимает одно и то же значение. Значит, наше предположение ложно, и, следовательно, каждому значению
соответствует более двух точек из отрезка [a, b], в которых функция принимает одно и то же значение. Значит, наше предположение ложно, и, следовательно, каждому значению 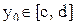 соответствует одно и только одно значение
соответствует одно и только одно значение  такое, что
такое, что 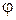 , по которому каждому значению
, по которому каждому значению  ставится в соответствие такое единственное число
ставится в соответствие такое единственное число 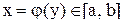 , которое удовлетворяет условию
, которое удовлетворяет условию 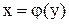 называется обратной по отношению к функции
называется обратной по отношению к функции 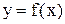 . Правило
. Правило 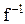 и записывают в виде
и записывают в виде 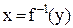 . Очевидно, графики функций
. Очевидно, графики функций  , то ее координаты удовлетворяют условию
, то ее координаты удовлетворяют условию 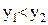 , т.е.
, т.е. 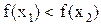 , то
, то 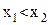 , ибо функция
, ибо функция 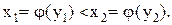 Аналогично рассматривается случай строго убывающей функции. На верхнем рисунке изображен график функции, которая не имеет обратной, хотя бы потому, что значению
Аналогично рассматривается случай строго убывающей функции. На верхнем рисунке изображен график функции, которая не имеет обратной, хотя бы потому, что значению 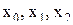 переменной х, при которых функция принимает значение
переменной х, при которых функция принимает значение 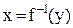 , которая определена на множестве ее значений,причем обратная функция строго возрастает,если функция
, которая определена на множестве ее значений,причем обратная функция строго возрастает,если функция  будем записывать в виде
будем записывать в виде 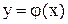 или
или 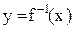 . В этом случае множества, на которых изменяются переменные х и у, меняются местами. Так, если для исходной функции
. В этом случае множества, на которых изменяются переменные х и у, меняются местами. Так, если для исходной функции  Если точка (х, у) принадлежит графику функции
Если точка (х, у) принадлежит графику функции 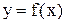 , то точка (у, х) будет принадлежать графику функции
, то точка (у, х) будет принадлежать графику функции  ,потому что зеркальным отражением произвольной точки (a, b) относительно прямой
,потому что зеркальным отражением произвольной точки (a, b) относительно прямой  является точка (b, a).
является точка (b, a). Функция
Функция  определена на бесконечном промежутке
определена на бесконечном промежутке 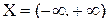 ,
, 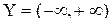 – множество ее значений. Так как данная функция является строго возрастающей на R, то она имеет обратную функцию
– множество ее значений. Так как данная функция является строго возрастающей на R, то она имеет обратную функцию  относительно переменнной
относительно переменнной 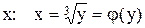 . Меняя х и у местами, получим привычную запись обратной функции в виде
. Меняя х и у местами, получим привычную запись обратной функции в виде 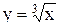 . Ее график симметричен кривой
. Ее график симметричен кривой 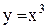 относительно прямой
относительно прямой  Функция
Функция  определена на бесконечном промежутке
определена на бесконечном промежутке , множество ее значений образует бесконечный промежуток
, множество ее значений образует бесконечный промежуток 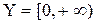 . Так как данная функция не является строго монотонной на Х (почему?), то она не имеет обратной функции.
. Так как данная функция не является строго монотонной на Х (почему?), то она не имеет обратной функции. Пусть D(f) – область определения функции
Пусть D(f) – область определения функции 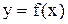 , а Х – подмножество области определения ее D(f). Функция
, а Х – подмножество области определения ее D(f). Функция 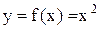 на промежуток
на промежуток 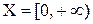 ,
, 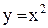 строго возрастает, и, следовательно, имеет обратную функцию. Решая уравнение
строго возрастает, и, следовательно, имеет обратную функцию. Решая уравнение 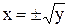 . Так как переменная х принимает неотрицательные значения (
. Так как переменная х принимает неотрицательные значения (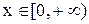 ), то
), то  . Меняя х и у местами, находим, что обратная функция задается формулой
. Меняя х и у местами, находим, что обратная функция задается формулой 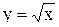 .
.  Рассматривая сужение функции
Рассматривая сужение функции  на множество
на множество 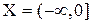 , найдем, что она удовлетворяет условиям существования обратной функции (как строго убывающая функция). Решая уравнение
, найдем, что она удовлетворяет условиям существования обратной функции (как строго убывающая функция). Решая уравнение 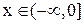 , то
, то  , откуда, находим, что обратная функция задается формулой (см.рисунок).
, откуда, находим, что обратная функция задается формулой (см.рисунок). ,
,  ?
?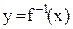 , если известен график функции
, если известен график функции 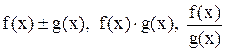 иметь обратную, если функция f(x) имеет обратную, а функция g(x) – не имеет? Приведите примеры.
иметь обратную, если функция f(x) имеет обратную, а функция g(x) – не имеет? Приведите примеры.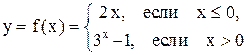 найти обратную функцию, построить график, указать область ее определения.
найти обратную функцию, построить график, указать область ее определения. Решение. Так как данная функция строго возрастает на числовой оси, то она имеет обратную функцию. Найдем ее. Если
Решение. Так как данная функция строго возрастает на числовой оси, то она имеет обратную функцию. Найдем ее. Если 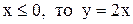 , причем, значения функции образуют бесконечный промежуток
, причем, значения функции образуют бесконечный промежуток 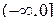 . Очевидно,
. Очевидно, 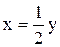 . Значит,
. Значит, 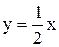 – «часть» обратной функции для
– «часть» обратной функции для 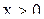 , тогда
, тогда  . Находим из последнего уравнения х:
. Находим из последнего уравнения х: 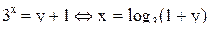 . Следовательно, функция
. Следовательно, функция 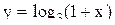 – еще одна «часть» обратной функции (или правильнее сказать еще одно ее сужение), причем,
– еще одна «часть» обратной функции (или правильнее сказать еще одно ее сужение), причем, 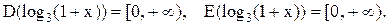 Объединяя полученные формулы в одну, получим обратную к исходной функции:
Объединяя полученные формулы в одну, получим обратную к исходной функции: 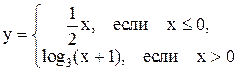 . Ее график изображен на рисунке пунктирной линией.. Он получен путем зеркального отображения исходной функции (симметрии) относительно прямой
. Ее график изображен на рисунке пунктирной линией.. Он получен путем зеркального отображения исходной функции (симметрии) относительно прямой  2.
2. 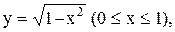 3.
3. 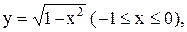
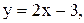 5.
5. 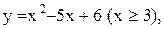 6.
6. 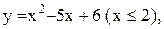
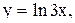 8.
8. 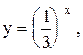 9.
9. 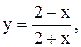
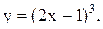 11.
11. 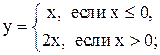 12.
12. 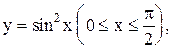
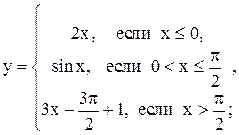 14.
14. 
 16.
16.  17.
17. 
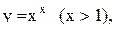 19.
19. 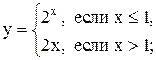 20.
20.