
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение любого конечного семейства открытых множеств есть открытое множество.
Доказательство. 1) Действительно, если точка а принадлежит объединению открытых множеств, то она принадлежит по крайней мере, одному из этих множеств, которое по условию теоремы является открытым. Значит, ему принадлежит некоторая окрестность О(а) точки а, но тогда эта окрестность принадлежит и объединению всех открытых множеств. Следовательно, точка а является внутренней точкой объединения. Так как а – произвольная точка объединения, то оно состоит лишь из внутренних точек, и, значит, по определению является открытым множеством. 2) Пусть теперь Х – пересечение конечного числа открытых множеств Из этой теоремы следует, что пересечение конечного числа окрестностей точки а есть опять окрестность этой точки. Заметим, что пересечение бесконечного числа открытых множеств не всегда является открытым множеством. Например, пересечением интервалов Точка а называется предельной точкой множества Х, если в любой проколотой окрестности Так, точка
Легко доказать, что каждая точка отрезка [ 0, 1] является предельной точкой данного отрезка. Другими словами, отрезок [0, 1] сплошь состоит из своих предельных точек. Аналогичное утверждение справедливо для любого отрезка. Заметим здесь, что все предельные точки множества [0, 1] принадлежат этому отрезку. Очевидно также, что все точки отрезка [0, 1], будут предельными точками для интервала (0, 1) (докажите!). Однако, здесь уже две предельные точки 0 и 1 не принадлежат интервалу (0, 1). На данных примерах мы видим, что
предельные точки множества могут принадлежать ему и могут не принадлежать. Можно доказать, что в любой проколотой окрестности Множество Х
Так, всякий отрезок есть замкнутое множество. Интервал (0, 1) не является замкнутым множеством, так как ему не принадлежат две его предельные точки 0 и 1. Множество всех рациональных чисел Q не является замкнутым, так как не содержит некоторые свои предельные точки. В частности, число Так как каждая точка множества R является предельной точкой этого множества и принадлежит ему, то R – замкнутое множество. Пустое множество условимся также считать замкнутым, так как оно содержит все свои предельные точки,которых у него нет. Всякое конечное множество является замкнутым, так как множество его предельных точек является пустым множеством Æ, которое принадлежит самому множеству. Замкнутые множества могут быть ограниченными, например, отрезок [0, 1], и неограниченными, например, множество действительных чисел R.Верна Теорема: 1) Объединение конечного числа замкнутых множеств есть замкнутое множество;
|
|||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 930; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.147.215 (0.006 с.) |
 . Если а есть точка множества Х, то она принадлежит каждому из открытых множеств
. Если а есть точка множества Х, то она принадлежит каждому из открытых множеств 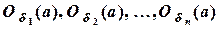 , которые целиком содержатся соответственно в множествах
, которые целиком содержатся соответственно в множествах 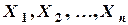 . Обозначим через
. Обозначим через 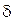 наименьшее из чисел
наименьшее из чисел 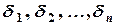 . Тогда интервал
. Тогда интервал 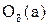 будет содержаться одновременно во всех интервалах
будет содержаться одновременно во всех интервалах 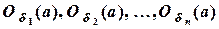 , т.е.
, т.е.  будет целиком содержаться и в
будет целиком содержаться и в 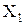 , и в
, и в 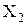 ,..., и в
,..., и в 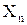 , т.е.
, т.е. 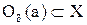 . Отсюд а заключаем, что любая точка является внутренней точкой множества Х, т.е. множество Х является открытым.
. Отсюд а заключаем, что любая точка является внутренней точкой множества Х, т.е. множество Х является открытым.
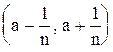 ,… является множеством, состоящее из одной точки а, которое, не является открытым множеством (почему?).
,… является множеством, состоящее из одной точки а, которое, не является открытым множеством (почему?).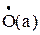 этой точки имеется, по крайней мере, одна точка множества Х.
этой точки имеется, по крайней мере, одна точка множества Х. является предельной точкой отрезка [0, 1], так как в любом проколотом интервале
является предельной точкой отрезка [0, 1], так как в любом проколотом интервале  точки
точки 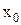 , удовлетворяющая неравенству
, удовлетворяющая неравенству  . И таких точек, очевидно, много.
. И таких точек, очевидно, много.

 предельной точки а множества Х имеется бесконечно много точек множества Х.
предельной точки а множества Х имеется бесконечно много точек множества Х. называется замкнутым множеством, если оно содержит все свои предельные точки.
называется замкнутым множеством, если оно содержит все свои предельные точки.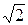 является предельной точкой множества Q (докажите!), но
является предельной точкой множества Q (докажите!), но  Q.
Q.


