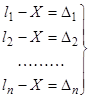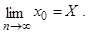Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сущность измерений. Виды погрешностей и методы борьбы с нимиСодержание книги
Поиск на нашем сайте Измерить какую-либо величину - это значит сравнить ее с однородной величиной, принятой за единицу измерения. Например, при измерении длин за единицу измерения принимают метр. Любое измерение всегда содержит некоторую погрешность. Безошибочных измерений в природе не существует. Для выявления этих погрешностей, ослабления их влияния на результат измерения и для оценки точности выполняются повторные и избыточные измерения. Обозначим через X истинное значение измеряемой величины, через l - результат измерения, через D - погрешность измерения. Тогда, очевидно, имеет место равенство D = l – X (8) Погрешность D всегда остается величиной неизвестной, поскольку всегда неизвестно истинное значение Х. Процесс измерения всегда происходит при наличии следующих факторов::инструмент, внешняя среда, человек. Каждый из этих факторов является носителем погрешностей. По своему характеру погрешности делятся на грубые, систематические и случайные. Грубые погрешности - это такие, которые допущены в результате грубых промахов человека, грубых неисправностейинструмента, резких изменений во внешней среде. Грубые погрешности необходимо выявить, а результаты измерений, содержащие их, отбраковать. Существует два метода борьбы с грубыми погрешностями: метод повторных измерений и метод избыточных измерений. Пример 1. Один и тот же угол был измерен пять раз (повторные измерения) с точностью 1¢ и получен следующий ряд результатов l6°12¢ ; 16°I3¢ ; I7°13¢; 16 ° 12¢. Поскольку абсолютно точных измерений в природе не существует, то разброс результатов измерений в 2¢-3¢ является естественным. Однако один результат (l7°13¢) резко отличается от других. Мы вправе сделать заключение, что он содержит грубую погрешность. Такой результат из ряда измерений вычеркивают. Зачастую можно определить и фактор, вызвавший грубую погрешность. В нашем примере таким фактором, скорее всего является человек. Пример 2. В треугольнике измерены углы с точностью 1¢: a = 45°34¢;b= 61°18¢; g =74°50¢. В принципе достаточно было бы измерить любых два угла, например, a и b, а угол g вычислить g = 180° - (a + b). Измерение третьего угла является лишним, но оно позволяет произвести контроль качества измерений (избыточное измерение) и выявить грубую погрешность. Действительно, в нашем примере a + b + g = 181° 42¢. При точности измерений 1¢ отличие этой суммы от теоретической 181° 42¢ - 180° = 1° 42' является слишком большим, и мы можем заключить, что в измерениях допущена грубая погрешность. Однако в этом случае указать конкретное измерение, содержащее грубую погрешность, затруднительно. Необходимо заново измерить все углы. Систематические погрешности - это такие, которые по определенному закону повторяются в многократных измерениях. Систематические погрешности возникают в результате влияния внешней среды, мелких и до конца неисправляемых погрешностей прибора и личных ошибок человека, обусловленных его индивидуальными особенностями. Они бывают большие и маленькие, постоянные и переменные, положительные и отрицательные. Их необходимо выявлять, учитывать и исключать. Существует два метода борьбы с систематическими погрешностями: метод введения поправки в результат измерения и подбор такой методики измерения, которая автоматически исключает систематическую погрешность или делает ее пренебрежимо малой. Пример 1. Известно, что при изменении температуры длина стальной рулетки изменяется. Это изменение длины можно заранее вычислить и внести соответствующую поправку в результат измерения. Подробно это будет рассмотрено в главе 7. Пример 2. При измерении углов прибором теодолитом существует методика "полного приема", а при измерении превышения прибором нивелиром - методика нивелирования "из средины". Обе эти методики позволяют автоматически исключить ряд систематических погрешностей. Подробно эти методики будут рассмотрены далее. Случайные погрешности являются результатом воздействия множества мелких факторов, учесть которые невозможно. Все три фактора (внешняя среда, прибор и человек) вносят свою лепту в образование суммарной случайной погрешности. Величину каждой в отдельности случайной погрешности узнать нельзя, но в своей совокупности они проявляют определенные закономерности, которые подробно изучаются в разделе высшей математики "Теория вероятностей и математическая статистика". Отметим некоторые свойства случайных погрешностей. 1. При данных условиях измерений одной и той же величины случайные погрешности не могут превосходить известного предела. 2. Равные по абсолютной величине положительные и отрицательные случайные погрешности встречаются одинаково часто. 3. Среднее арифметическое из случайных погрешностей стремится к нулю при неограниченном увеличении числа измерений. Пусть D1, D2, …, D n - случайные погрешности, тогда согласно этому свойству
Обозначим D1 + D2 + … + D n = [D], тогда это свойство можно записать
(9)
4. Малые по абсолютной величине случайные погрешности встречаются чаще, чем большие.
График функции асимптотически стремится и оси X. Это означает, что большие D встречаются очень редко. Практически можно считать, что за пределами скобок случайные погрешности не встречаются. Величину этого предела (3m), о котором идет речь в первом свойстве, укажем позднее. Иллюстрация второго свойства очевидна, так как график функции симметричен относительно оси Y. По этой же причине очевидно и третье свойство. Метода борьбы с каждой в отдельности случайной погрешностью не существует. Однако, в ряде повторных измерений существует возможность значительно ослабить влияние случайных погрешностей в окончательном результате. Этот метод борьбы со случайными погрешностями носит название принципа арифметической средины. Рассмотрим его подробнее. Пусть X - истинное значение измеряемой величины, l 1 , l2, … ln, - результаты измерений, D1,, D2, …, Dn - случайные погрешности. Согласно (8)
(10)
Сложим эти равенства и разделим почленно на n.
(11)
Обозначим [ l ]/ n = x0. Очевидно, что x 0 - это среднее арифметическое из результатов измерений. Перейдем в (11) к пределу при n ® ¥
(11)
Согласно третьему свойству случайных погрешностей
Поэтому (12)
Это означает, что в пределе среднее арифметическое x0 равно истинному значению X. На практике число повторных измерений п всегда ограничено. Поэтому полностью суммарная случайная погрешность в окончательном результате x0 не исключается, но значительно ослабляется и тем сильнее, чем больше повторных измерений n. Это и есть единственный метод борьбы со случайной погрешностью, носящий название принципа арифметической средины. Результаты измерений всегда содержат случайные и систематические погрешности, а иногда еще и грубые. Искусство математической обработки состоит в том, чтобы сделать отбраковку результатов, содержащих грубые погрешности, выявить систематические и свести их влияние к минимуму, и значительно ослабить влияние случайной погрешности. В дальнейшем изложении будем считать, что грубые и систематические погрешности выявлены и устранены и результаты измерений содержат только случайные погрешности.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 1023; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |
||||||||||||||||||||||||||||||


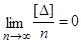
 Поведение случайных погрешностей подчиняется закону нормального распределения. График дифференциальной функции этого закона приведен на рис.3.1. График прекрасно иллюстрирует все четыре свойства случайных погрешностей. По оси X откладывается величина случайной погрешности D,по оси Y - частота их появления.
Поведение случайных погрешностей подчиняется закону нормального распределения. График дифференциальной функции этого закона приведен на рис.3.1. График прекрасно иллюстрирует все четыре свойства случайных погрешностей. По оси X откладывается величина случайной погрешности D,по оси Y - частота их появления.