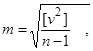Средняя квадратическая погрешность одного измерения

После выполненных измерений всегда необходимо оценить их точ­ность. Оценку точности можно сделать только тогда, когда есть пов­торные или избыточные измерения. Существуют различные критерии точности. Наиболее удобным и естественным критерием является дисперсия D, характеризующая меру рассеяния результатов измерений. Поскольку на практике число повторных измерений всегда конечно, приходится ограничиваться приближенным значением ее, носящим наз­вание оценки дисперсии. Она вычисляется по формуле

(13)

 

где D₁, D₂, …, D _n -случайные погрешности в результатах измере­ний одной и той же величины. В математической статистике доказыва­ется, что оценка (13) является состоятельной, эффективной и несме­щенной. Определенным неудобством в использовании этой оценки явля­ется её квадратическая размерность по сравнению с результатамииз­мерений. Для избежания этого неудобства используют критерий точ­ности 

                          или                                                   (14)                                                                   

 

носящей название средней квадратической погрешности. Она обладает рядом достоинств.

I. При числе измерений n ³ 9 величина т изменяется очень мало и, следовательно, значение т  близко к её теоретическому аналогу - стандарту s. При числе измерений n<9 критерий точности т сле­дует считать ненадёжным.

2. Из опыта установлено, что в ряду, состоящем из 1000 изме­рений, лишь три случайные погрешности превосходят величину 3 m. Следовательно, её можно принять за предельную погрешность Δ _пред, т.е.

Δ _пред = 3 m.

Величина 3 m и является тем пределом, о котором речь шла в первом свойстве случайных погрешностей. Предельная погрешность играет важную роль при установлении допусков в различных нормативных до­кументах, так как 3 m принимают за допустимую погрешностьΔ _доп  , т.е.

Δ _доп = Δ _пред = 3 m.

При увеличении числа измерений надёжность найденной по форму­ле (14) погрешности возрастает. В теории погрешностей измерений до­казывается, что погрешность т _m определения самой погрешности приб­лижённо можно найти по формуле

 

 

 

В заключение подчеркнем, что погрешность m служит критерием точности одного измерения, характерного для всей группы выполнен­ных измерений

Формула Бесселя

Критерий точности m, введённый по формуле (14), на прак­тике имеет ограниченное применение, так как случайные погрешности Δ _i остаются неизвестными. Для той же самой средней квадратической погрешности m можно вывести формулу с использованием арифметичес­кой средины x₀

(15)

где v_i = l_i – x₀, x₀ = (l₁ + l₂ + … + l_n) / n, l_i – результаты измерений. Формула (15) носит название формулы Бесселя и применяется на практике для оценки точности.