
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние кривизны Земли на угловые, линейные и высотные измеренияСодержание книги
Поиск на нашем сайте ОГЛАВЛЕНИЕ ОГЛАВЛЕНИЕ.. 3 1. ВВОДНАЯ ЧАСТЬ. 7 1.1. Задачи геодезии. 7 1.2. Понятие о фигуре Земли. 8 1.3. Влияние кривизны Земли на угловые, линейные и высотные измерения 9 1.4. Системы координат, применяемые в геодезии. 12 1.4.1. Географическая система координат. 12 1.4.2. Плоская прямоугольная система координат. 13 1.4.3. Полярная система координат. 13 2. ТОПОГРАФИЧЕСКИЕ ПЛАНЫ И КАРТЫ... 15 2.1. Понятие о плане и карте. 15 2.2. Масштаб. 15 2.3. Понятие о картографической проекции Гаусса-Крюгера. 17 2.4 Номенклатура топографических карт. 20 2.5. Ориентирование линий местности. 22 2.6. Изображение рельефа местности на топографических картах 25 2.7. Решение некоторых задач на карте с помощью горизонталей 27 2.7.1. Определение высот точек: 27 2.7.2. Определение крутизны ската. 28 2.8. Условные знаки на топографических картах. 29 2.9. Понятие об электронной карте. 30 3. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ 31 3.1. Сущность измерений. Виды погрешностей и методы борьбы с ними 31 3.2. Средняя квадратическая погрешность одного измерения. 36 3.3. Формула Бесселя. 37 3.4. Средняя квадратическая погрешность функций измеренных величин 38 3.5. Понятие о двойных измерениях. 39 3.6. Понятие о неравноточных измерениях. 41 4. ПОНЯТИЕ О ГОСУДАРСТВЕННОЙ ГЕОДЕЗИЧЕСКОЙ СЕТИ 43 4.1. Плановая Государственная геодезическая сеть. 43 4.2. Высотная Государственная геодезическая сеть. 45 4.3. Понятие о спутниковых навигационных системах. 45 5. УГЛОВЫЕ ИЗМЕРЕНИЯ.. 48 5.1. Части геодезических приборов. 48 5.1.1. Цилиндрический уровень. 48 5.1.2. Зрительная труба. 49 5.1.3. Угломерные круги. 50 5.2. Классификация теодолитов. 51 5.3. Принцип измерения горизонтального угла. 51 5.4. Общее знакомство с теодолитом 2Т30. 52 5.5. Понятие о поверках теодолита. 57 5.5.1. Оси теодолита. 57 5.5.2. Схема проведения поверок. 58 5.6. Поверка цилиндрического уровня. 58 5.7. Поверка коллимационной ошибки. 61 5.8. Поверка перпендикулярности оси вращения трубы и оси вращения теодолита 63 5.9. Поверка сетки нитей. 64 5.10. Измерение горизонтального угла методом полного приема 65 5.11. Влияние установки прибора и вех на измеряемое направление 67 5.12. Измерение углов наклона. 68 6. ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ.. 70 6.1. Измерение расстояний мерными лентами и рулетками. 70 6.2. Измерение расстояний физико-оптическими дальномерами. 72 6.3. Понятие о светодальномерах. 75 7. ИЗМЕРЕНИЕ ПРЕВЫШЕНИЙ.. 77 7.1. Сущность и методы геометрического нивелирования. 77 7.2. Последовательное нивелирование. 79 7.3. Классификация нивелиров. 80 7. 4. Устройство нивелира Н3. 80 7.5. Поверки нивелира Н3. 83 7.5.1. Поверка круглого уровня. 83 7.5.2. Поверка главного условия. 84 7.5.3. Поверка сетки нитей. 86 7.6. Нивелирные рейки. 87 7.7. Порядок работы на станции нивелирования. 88 7.8. Основные источники погрешностей при геометрическом нивелировании 89 7.9. Прокладка нивелирного хода. 93 7.10. Техническое нивелирование. 96 7.11. Тригонометрическое нивелирование. 96 7.12. Гидростатическое нивелирование. 98 8. ГЕОДЕЗИЧЕСКОЕ СЪЕМОЧНОЕ ОБОСНОВАНИЕ.. 100 8.1. Теодолитные ходы.. 100 8.2. Математическая обработка замкнутого теодолитного хода. 101 8.3. Математическая обработка разомкнутого теодолитного хода 105 9. ТОПОГРАФИЧЕСКИЕ СЪЕМКИ.. 108 9.1. Теодолитная съемка. 108 9.1.1. Способ прямоугольных координат. 109 9.1.2. Способ полярных координат. 109 9.1.3. Способ угловой засечки. 109 9.1.4. Способ линейной засечки. 110 9.2. Нивелирование поверхности. 111 9.3. Продольное нивелирование. 112 9.4. Тахеометрическая съемка. 114 9.5. Понятие о других видах съемки. 117 10. Геодезические работы в строительстве.. 120 10.1. Инженерно-геодезические изыскания. 120 10.2. Понятие о ППГР. 121 10.3. Разбивочные работы.. 122 10.3.1. Виды разбивочных работ. 122 10.3.2. Элементы разбивочных работ. 123 10.3.3. Решение обратной геодезической задачи. 127 10.3.4. Способы разбивочных работ. 127 10.3.5. Закрепление осей сооружений. 130 10.3.6. Передача отметки на дно котлована. 131 10.3.7. Разбивочные работы при монтаже сборных фундаментов. 132 10.3.8. Разбивочные работы при монтаже железобетонных и металлических колонн 133 10.3.9. Разбивочные работы при монтаже балок. 134 10.4. Исполнительные съемки. 135 10.5. Понятие о смещениях и деформациях инженерных сооружений в процессе эксплуатации 136 Заключение.. 139 Библиографический список.. 139 Предметный указатель. 140 ВВОДНАЯ ЧАСТЬ Задачи геодезии Геодезия – это наука об измерениях на земной поверхности и их математической обработке с целью решения различных задач. При этом приборы и сами измерения называются геодезическими. Основными геодезическими измерениями являются: угловые (измерения горизонтальных и вертикальных углов); линейные (измерения горизонтальных расстояний); высотные (измерение превышений между точками). Все решаемые геодезией задачи можно разделить на научные и научно-практические. Научные задачи: 1. Определение размеров, фигуры Земли и ее внешнего гравитационного поля. Эти данные необходимы, в частности, для расчета орбит ИСЗ и межпланетных кораблей. 2. Определение движения материков и отдельных частей земной коры. Эта задача решается для целей прогноза землетрясений. 3. Изучение размеров, фигуры и создания карт планет Солнечной системы. 4. Составление карт дна шельфа с целью разведки и добычи полезных ископаемых. Эти и другие задачи решаются в разделе высшей геодезии. Все практические задачи геодезии применительно к специальностям строительного профиля связаны с изысканием, проектированием, строительством и эксплуатацией инженерных сооружений. Раздел геодезии, решающий эти задачи, называется инженерной геодезией. Основными перспективными проблемами ее являются: 1. Совершенствование методов измерений и приборов с целью полной автоматизации геодезических работ. 2. Создание банков информации, хранящейся в памяти ЭВМ, о всех геометрических параметрах инженерных сооружений. Понятие о фигуре Земли Если бы Земля была неподвижным однородным телом, она имела бы форму шара радиуса R = 6372 км. Под действием центробежной силы, вызванной вращением вокруг оси, однородная Земля окажется сплюснутой у полюсов и примет форму эллипсоида вращения (рис.1.1), характеризующегося большой полуосью а и малой полуосью b. На такой поверхности направления силы тяжести и нормали в каждой точке совпадают.
Для математической обработки геодезических измерений поверхность геоида ввиду ее сложности непригодна. Для этих целей выбирают более простую поверхность, близкую к геоиду. Такой поверхностью является эллипсоид вращения, соответствующих размеров и соответствующим образом расположенный в теле Земли. В нашей стране размеры эллипсоида были получены в 1940 г. под руководством выдающегося ученого Ф.Н.Красовского. Для этого эллипсоида сжатие
Заметим, что для шара сжатие α = 0, и, следовательно, земной эллипсоид мало отличается от шара. При решении задач высшей геодезии все измерения, выполненные на земной поверхности, относят к поверхности эллипсоида с учетом его отклонений от геоида. В инженерно-геодезической практике эти поверхности можно считать совпадающими не только между собой, но и с поверхностью шара. Более того, во многих случаях практики поверхность небольших участков Земли можно принять за плоскость. Полярная система координат При геодезических измерениях в инженерной практике часто используют полярную систему координат на плоскости, представляющую собой начало системы – полюс О и полярную ось ОХ (рис.1.7). Положение любой точки А в этой системе определяется полярным углом j и длиной r радиуса-вектора ОА. Применение других известных систем координат в инженерно-геодезической практике весьма ограничено.
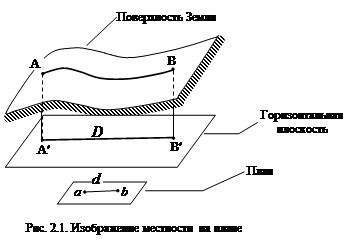
ТОПОГРАФИЧЕСКИЕ ПЛАНЫ И КАРТЫ 2.1. Понятие о плане и карте Определение. Топографическим планом называется уменьшенное подобное изображение небольших участков местности на бумаге. При этом кривизной Земли пренебрегают. Поверхность сферы невозможно развернуть на плоскость без разрывов и складок. Другими словами, поверхность Земли нельзя изобразить на бумаге без искажений. Для переноса точек с шаровой поверхности Земли на плоскость используют различные математические законы, которые называются картографическими проекциями. Любая картографическая проекция имеет искажения либо линейные, либо угловые, либо те и другие. Определение. Топографической картой называется уменьшенное согласно выбранной картографической проекции изображение больших участков земной поверхности. Ниже познакомимся с одной из таких картографических проекций, которая применяется в геодезии. Масштаб Одним из основных понятий плана и карты является понятие масштаба. Определение. Масштабом называется отношение длины линии d на плане или карте к длине горизонтальной проекции D той же линии на местности. Горизонтальной проекцией D (рис.2.1) называется ортогональная проекция линии AB местности на горизонтальную плоскость. Согласно определению масштаб равен d: D. Обычно это выражение записывают в виде простой дроби 1: D/ d = 1:М и тогда ее знаменатель М означает степень уменьшения. Например, для масштабов 1:500; 1:1000; 1:2000 степень уменьшения составляет соответственно 500, 1000 и 2000 раз. Такой масштаб называется численным.
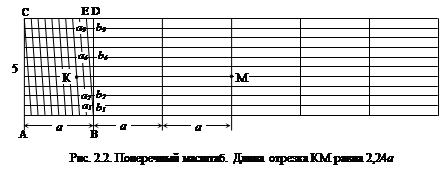
При откладывании линий на плане возникает вопрос о минимальном отрезке, который можно отложить или измерить без применения увеличительных приборов. Из опыта установлено, что человеческий глаз в среднем способен различить минимальный отрезок на бумаге длиной 0,1 мм. Такой размер имеет диаметр точки, полученный от накола остро отточенной иглой на листе ватмана. Этому минимальному расстоянию на планах различных масштабов соответствуют различные расстояния на местности. Например, для плана масштаба 1:500 0,1 мм соответствует на местности горизонтальному расстоянию D = 0,1 мм ´ 500 = 0,05 м. Определение. Длина горизонтальной линии D на местности, соответствующая 0,1 мм на карте или плане данного масштаба, называется точностью данного масштаба. В связи с этим возникает вопрос как достичь на бумаге графической точности 0,1 мм. Заметим, что обычная линейка с ценой деления 1 мм может обеспечить точность 0,5 мм. Высокая графическая точность достигается с помощью специальной линейки, которая называется поперечным масштабом (рис.2.2). Произвольный отрезок а называется основанием масштаба. Основания АВ и СD делят на 10 равных частей и точки деления соединяют наклонными прямыми, как показано на рисунке. Отрезки AС и BO также делят на 10 равных частей и точки деления соединяют параллельными горизонтальными прямыми. В результате такого построения
AA1 = A1A2 = A2A3 = … =0,1 a; E1B1 = 0,01 a, E2B2 = 0,02 a, …, E9B9 = 0,09 a. Например, длина отрезка KM равна a + a + 0,2 a + 0,04 а = 2,24 a. Обычно длину отрезка a берут равной 2 см. Тогда длина линии KMна плане масштаба 1:500 будет соответствовать горизонтальной линии на местности длиной 2,24 ´ 2 см ´ 500 = 22,4 м. Тот же отрезок на плане масштаба 1:1000 соответствует на местности D = 2,24 ´ 2 см ´ 1000 = 44,8 м. Определение крутизны ската Пусть на карте имеется отрезок между двумя горизонталями длиною а (рис.2.18), называемый заложением. Внизу приведен вид сбоку. Из треугольника ВСС′ имеем а = h • сtg a, где h - сечение рельефа: a - угол ската. Hа рис. 2.19 приведен
график этой функции, который называется масштабом заложения. н позволяет определить угол ската a линии ВС на карте. Для приведенного рисунка a» 1,3°. С помощью горизонталей на карте можно решать ряд других задач.
Формула Бесселя Критерий точности m, введённый по формуле (14), на практике имеет ограниченное применение, так как случайные погрешности Δ i остаются неизвестными. Для той же самой средней квадратической погрешности m можно вывести формулу с использованием арифметической средины x0
(15) где vi = li – x0, x0 = (l1 + l2 + … + ln) / n, li – результаты измерений. Формула (15) носит название формулы Бесселя и применяется на практике для оценки точности. Плановая Государственная геодезическая сеть Плановая ГГС создается методом триангуляции, трилатерации и полигонометрии (рис.4.1). Триангуляция (рис.4.1, а) представляет собой ряд треугольников, в которых измерены все углы и концевые стороны (базисы) АВ и CD. Из астрономических измерений вычисляют
широту и долготу точек A, B, C, D, а также азимуты базисов. Решая последовательно треугольники A–B – 1, затем B - 1-2, и т.д., находят широты и долготы точек 1, 2, 3,... и длины сторон всех треугольников. После этого в проекции Гаусса-Крюгера переходят к прямоугольным координатам (Х, Y) этих точек в единой системе координат. Если в цепи треугольников вместо углов измерены все стороны, то такое построение называется трилатерацией. Полигонометрия (рис.4.1, б) представляет собой разомкнутый или замкнутый многоугольник, в котором измерены все стороны и углы. Пункты плановой ГГС надёжно закрепляются на местности. Для обеспечения взаимной видимости между пунктами над ними устанавливают геодезические сигналы (вышки). По своей точности плановая ГГС делится на четыре класса. Сеть 1 класса строится в виде рядов треугольников со сторонами 20-25 км. Ряды располагаются вдоль меридианов и параллелей, образуя замкнутый полигон в виде четырехугольника периметром 800-1000 км. Аналогично строится полигонометрический ход 1 класса. Таблица 2
Внутри полигонов 1 класса и самих треугольников строится сплошная сеть треугольников или полигонометрии 2 класса с длинами сторон от 7 до 20 км. Дальнейшее сгущение сети производится построением пунктов 3 и 4 классов с длинами сторон 5-8 км. Точностные характеристики перечисленных классов точности ГГС приведены в таблице 2. В этой таблице под точностью измерения углов понимается средняя квадратическая погрешность m b, а под точностью измерения сторон - относительная средняя квадратическая погрешность mS / S. УГЛОВЫЕ ИЗМЕРЕНИЯ Угловые измерения (измерения горизонтальных и вертикальных углов) необходимы при создании ГГС, для выполнения топографических съемок местности и решении многих геодезических задач при строительстве инженерных сооружений Точность измерения углов характеризуется их средней квадратической погрешностью. Для знакомства с приборами, применяемыми.в угловых измерениях, целесообразно вначале изучить отдельные их части. Цилиндрический уровень Он предназначен для приведения осей теодолита в горизонтальное и вертикальное положения. Уровень представляет собой стеклянную трубку, верхняя часть которой изогнута по дуге окружности радиуса R (рис.5.1, а).
Трубка наполнена легкой жидкостью (спирт, эфир). Небольшое свободное пространство, заполненное парами этой жидкости, выглядит в виде пузырька. Поскольку пары всегда легче жидкости, то пузырек имеет свойство занимать всегда наивысшее положение в трубке. Точка в средней части, ампулы называется нуль-пунктом. На наружной части ампулы нанесены деления. Если концы пузырька расположены симметрично относительно нуль-пункта, то говорят, что пузырек находится в нуль-пункте (рис.5.1, а, б). Определение. Осью цилиндрического уровня UU1 называется касательная к дуге ампулы в точке нуль-пункта. Можно доказать, что если пузырек находится в нуль-пункте, то ось уровня UU1занимает горизонтальное положение (рис.5.1, а). И наоборот, если пузырек не в нуль-пункте, то ось уровня наклонна к горизонту (рис.5.1, в). Таким образом, для приведения оси уровня UU1в горизонтальное положение необходимо привести пузырек уровня в нуль-пункт. В дальнейшем при работе с теодолитом выполнение этой операции будет требоваться постоянно. Точность уровня тем выше, чем больше радиус R. Изготавливают различной точности уровни с ценой деления от 10" до 2'. Зрительная труба Она предназначена для увеличения разрешающей способности глаза и точного наведения теодолита на точки местности. В простейшем случае зрительная труба имеет две линзы: объектив и окуляр (рис.5.2, а). В современных геодезических инструментах применяются зрительные трубы с внутренней фокусировкой. Между объективом и окуляром ставится двояковогнутая линза, перемещающаяся внутри трубы с помощью кремальеры. Изменение положения этой линзы меняет положение фокуса объектива, поэтому она называется фокусирующей линзой.
В окулярной части трубы находится стеклянная пластинка с нанесенными взаимно-перпендикулярными штрихами 3 (рис.5.2, а, б) которая называется сеткой нитей. Центральная точка К называется перекрестьем сетки нитей. Важнейшим понятием для зрительной трубы является ее визирная ось. Определение. Визирной осью W W1 называется прямая, проходящая через оптический центр объектива точку О и перекрестье сетки нитей К. Навести трубу (теодолит) на точку местности - это значит совместить ее с визирной осью. При этом точка будет видна в перекрестье сетки нитей. Угломерные круги Угломерные круги служат рабочей мерой для измерения углов. Угломерный круг, предназначенный для измерения горизонтальных углов, называется лимбом, а для измерения вертикальных углов - вертикальным кругом. В принципе угломерные круги - это круговые транспортиры, сделанные из стекла, с точно нанесенными градусными и минутными делениями. Ввиду хрупкости и возможного загрязнения угломерные круги в теодолите закрывают металлическими кожухами. Для отсчитывания дуг на угломерных кругах применяются отсчетные приспособления. В теодолите имеются различные винты. По своему назначению их можно разделить на следующие виды: - закрепительные винты, служащие для закрепления вращающихся частей теодолита; - наводящие или микрометренные винты, служащие для плавного и медленного перемещения тех же вращающихся частей; - исправительные или юстировочные винты, служащие для изменения взаимного расположения осей теодолита; - три подъемных винта, на которых установлен теодолит, служат для приведения оси теодолита в вертикальное положение (рис.5.4). Классификация теодолитов В нашей стране теодолиты выпускаются в соответствии с ГОСТ 10529 - 86. Стандарт устанавливает основные типы теодолитов: - высокоточные Т05, Т1; - точные Т2, Т5; - технические T15, T30. Буква в шифре прибора означает его название - теодолит, а число - точность в секундах дуги. Теодолиты 2ТЗ0, 3Т30, 4Т30, 5Т30 представляют модификацию теодолита ТЗ0. Все эти теодолиты широко применяются на строительных площадках. Если шифр прибора заканчивается буквой М, например Т30М, теодолит маркшейдерский – предназначен для работы в подземных выработках, если шифр заканчивается буквой П, например 4Т30П, труба прибора дает прямое, а не перевернутое изображение. Оси теодолита В процессе поверок участвуют следующие оси теодолита: - ось цилиндрического уровня (UU1); - визирная ось зрительной трубы (WW1); - ось вращения теодолита (ZZ1); - ось вращения трубы (HH1). В скобках приведены общепринятые обозначения осей. Первые две оси UU1 и WW1 были определены ранее. Осью вращения теодолита называется воображаемая прямая, вокруг которой вращается теодолит. Осью вращения трубы HH1 называется воображаемая прямая, вокруг которой вращается труба. В ходе поверок участвует также одна из нитей сетки. Схема проведения поверок При проведении поверок полезно придерживаться следующей схемы, обеспечивающей целостное понимание существа вопроса: - формулировка требуемого геометрического условия; - выяснение необходимости этого условия; - порядок выполнения поверки, т.е. описание действий, в результате которых становится ясно - выполняется или не выполняется требуемое условие; - порядок исправления положения одной из осей, если будет выяснено, что требуемое условие не выполняется. В теодолите 2Т30 существует четыре основных поверки. Порядок изучения их не является существенным. Поверка сетки нитей
Невыполнение этого условия приводит к перекосу сетки нитей, что затрудняет наведение трубы на точки местности, вехи и рейки. Для проверки выполнения этого условия выбирают на местности точку А и наводят на нее среднюю нить сетки (рис.5.14, б). Плавно поворачивают теодолит вокруг оси ZZ1. При этом точка А будет перемещаться в поле зрения трубы. Если точка А будет оставаться на нити, значит требуемое условие выполняется. Если точка А займет положение А1 или А2, значит условие не выполнено. Отклонение точки А от нити допускается не более 1/3 ширины биссектора (двойной нити). Исправление перекоса производится поворотом сетки нитей. Замечание. При проведении поверок теодолита, за исключением поверки цилиндрического уровня, приведение оси вращения теодолита в вертикальное положение не требуется. Все поверки являются независимыми друг от друга, поэтому порядок их выполнения не является существенным. Однако после поверки сетки нитей следует еще раз повторить поверку коллимационной ошибки или проводить ее вообще последней. Измерение углов наклона
При наведении на точку 1 отсчет по вертикальному кругу (КЛ)окажется ошибочным на величину М0 (рис.5.19, б). Очевидно, что угол наклона α = КЛ – М0. (30) При положении теодолита "круг право" при наведении на эту же точку α = М0 - КП (31) Складывая и вычитая равенства (30) и (31), получим
(32)
(33) Для вычисления α можно пользоваться любой из 3-х формул (30), (31), (32). Для удобства работы М0 делают равным нулю. Вначале вычисляют α по формуле (32) и при положении теодолита «круг лево» устанавливают по вертикальному кругу отсчет, равный α. При этом крест сетки нитей уйдет с точки 1. Исправительными винтами сетки крест вновь наводят на точку. Замечание. Формулы (30) - (33) справедливы для теодолита 2Т30, а для теодолитов иной конструкции могут быть другими. Такие сведения обязательно содержатся в прилагаемом к теодолиту паспорте. ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ Расстояния между точками местности можно измерять непостредственно и косвенно. Непосредственные измерения производятся с помощью стальных мерных лент и рулеток. При косвенном методе измеряются какие-то другие величины, а расстояние вычисляется как функция этих измеренных величин. Понятие о светодальномерах Во всех светодальномерах принята одна и та же принципиальная блок-схема. Дальномер состоит из двух основных частей: приемо-передатчик, устанавливаемый в начальной точке А и отражатель, устанавливаемый в конечной точке B (рис.6.6).
(50)
где v - скорость света в воздухе в момент измерения.
В современных светодальномерах измеряется не время τ, а разность фаз между опорной волной, поступающей в приемник непосредственной из передатчика, и отраженной волной. Это позволяет увеличить точность измерений на 2-3 порядка. Средняя квадратическая погрешность в определении расстояний светодальномерами равна 2-5 мм, а относительная порядка 1: 500000. Достоинствами светодальномеров является их надежность, высокая точность и возможность измерения расстояний в широком диапазоне - от нескольких метров до десятков километров в любое время суток. К определённым недостаткам можно отнести то, что скорость электромагнитных волн v зависит от параметров атмосферы, которые необходимо достаточно точно знать на всем протяжении вдоль измеряемой линии.
ИЗМЕРЕНИЕ ПРЕВЫШЕНИЙ При решении многочисленных задач в инженерной практике необходимо знать высоты (отметки) точек. С этой целью производят нивелирование, т.е. определяют превышения точек местности и по известной отметке одной из них вычисляют отметки остальных точек. Существуют следующие способы нивелирования: - геометрическое нивелирование, в котором для измерения превышения используется горизонтальный визирный луч, задаваемый прибором нивелиром; - тригонометрическое нивелирование, в котором используется наклонный визирный луч, задаваемый теодолитом; - гидростатическое нивелирование, основанное на законе сообщающихся сосудов. Другие известные способы нивелирования имеют в строительной практике весьма ограниченное применение. Классификация нивелиров Нивелиры по точности делятся на три группы: - высокоточные,имеющие среднюю квадратическуа погрешность mh на 1 км двойного хода 0,5-2,0 мм. Представителями этой группы являются нивелиры Н05; Н1; Н2; - точные, имеющие mh порядка 3 мм (Н3); - технические, имещие mh» 10 мм (Н10). По конструкции нивелиры можно разделить на две группы: - нивелиры, визирная ось которых приводится в горизонтальное положение с помощью цилиндрического уровня (Н05, H1, Н2, Н3, Н10); - нивелиры, визирная ось которых приводится в горизонтальное положение автоматически, с помощью специального устройства, назывемого компенсатором (Н05К, НЗК, Н10К - отечественные; Ni 002, Ni 007 - производства Германии; Ni-B1 ¸ Ni-B6 - пpоизводcтвa Венгрии). Нивелиры, снабженные лимбом для измерения горизонтальных углов, имеют в своем шифре кроме того еще букву Л (НЗКЛ, 2Н10КЛ). Устройство нивелира Н3 Все нивелиры с цилиндрическими уровнями принципиально имеют одинаковое устройство и отличаются только точностными характеристиками. Поэтому познакомимся подробно с устройством нивелира Н3, получившим широкое применение в инженерно-строительной практике (рис.7.5). Основными частями нивелира являются: - зрительная труба (1) и скрепленный с ней цилиндрический уровень (2). Вся верхняя часть нивелира вместе с трубой свободно вращается вокруг оси нивелира ZZ1. Вращение фиксируется закрепительным винтом (3). Для плавного вращения служит наводящий винт (4). Кроме того, труба вместе с цилиндрическим уровнем в небольших пределах (15') поворачивается в вертикальной плоскости с помощью элевационного винта (5) (рис.7.5, б);
- круглый уровень (6) играет вспомогательную роль и служит для приведения оси нивелира ZZ1, в вертикальное положение; - подставка с тремя подъемными винтами (7). Цилиндрический уровень снабжен призменным устройством, передающим изображение концов пузырька в поле зрения трубы. Положению пузырька уровня в нуль-пункте соответствует оптический контакт концов его половинок (рис.7.6, а).
При наклоне оси уровня UU1 контакт нарушается (рис.7.6, б).
Осью круглого уровня VV1 называется перпендикуляр к сферической поверхности в точке нуль-пункта. Очевидно, что при положении пузырька в нуль-пункте ось уровня VV1 занимает отвесное положение. При соответствующей юстировке в этом случае в поле зрения трубы появляется изображение концов половинок пузырька цилиндрического уровня, а совмещение их достигается вращением элевационного винта. Конструкция нивелира предусматривает параллельность визирной оси и оси цилиндрического
уровня (рис.7.8, а). После приведения пузырька цилиндрического уровня в нуль-пункт ось уровня UU1 займет горизонтальное положение и, следовательно, визирная ось тоже (рис.7.8, б). У нивелиров с самоустанавливающейся (в горизонтальное положение) линией визирования цилиндрический уровень и элевационный винт отсутствуют. Их заменяет компенсатор, представляющий собой две прямоугольные призмы, устанавливающиеся под действием силы тяжести маятника в положение, при котором визирный луч сохраняет горизонтальность при небольших наклонах трубы. Этот рабочий диапазон компенсатора обеспечивается круглым уровнем. Поверки нивелира Н3 Для обеспечения правильной работы нивелира в нем должны выполняться конструктивно заложенные геометрические условия между его осями. Оси нивелира: - ось вращения нивелира ZZ1; - ось цилиндрического уровня UU1; - визирная ось WW1; - ось круглого уровня VV1. Выполнение или невыполнение требуемых условий выясняется в ходе поверок. При описании поверок будем придерживаться схемы, приведенной в разделе "поверки теодолита". Поверка круглого уровня Ось круглого уровня VV1 должна быть параллельна оси вращения нивелира ZZ1(рис.7.9, а). Это условие необходимо для приведения оси вращения нивелира в вертикальное положение. Действительно, если условие VV1║ZZ1 выполняется, то после приведения пузырька уровня в нуль-пункт (рис.7.9, б) ось уровня VV1 займет вертикальное положение и, следовательно, ось ZZ1 - тоже. В свою очередь, вертикальность оси ZZ1 нужна для обеспечения такого диапазона работы элевационного винта, внутри которого пузы Порядок выполнения поверки следующий. Тремя подъемными винтами выводят пузырек уровня в нуль-пункт и поворачивают нивелир на 180˚. Если при этом пузырек остается в нуль-пункте, то условие выполняется. Если пузырек ушел из нуль-пункта, то условие не выполняется. В последнем случае необходимо произвести юстировку. Исправляют положение оси уровня. Для этого исправительными винтами перемещают пузырек в сторону нуль-пункта на половину отклонения. Поверка главного условия Ось цилиндрического уровня UU1должна быть параллельна визирной оси WW1 (UU1 | | WW1) (рис. 7.8, а). Это условие необходимо для приведения визирной оси в горизонтальное положение. Действительно, если условие UU1||WW1 выполняется, то после приведения пузырька уровня в нуль-пункт (рис.7.8, б), ось уровня UU1 займет горизонтальное положение и, следовательно, визирная ось WW1 - тоже. Поверку можно выполнить двумя способами. Первый способ. На местности закрепляют кольями точки А и B на расстоянии 50-75 м. Нивелир устанавливают над точкой А и рейкой или рулеткой измеряют его высоту i (рис.7.10, а). Пузырек круглого уровня приводят в нуль-пункт и наводят трубу на рейку в точке В. Элевационным винтом выводят пузырек
цилиндрического уровня в нуль-пункт, после чего ось UU1 займет горизонтальное положение. Приступая к поверке, мы не знаем, выполняется или не выполняется требуемое условие Поэтому предположим, что условие не выполняется, и тогда визирная ось WW, будет наклонена к горизонту, например, как на рис.7.10, а. Возьмем по рейке отсчет b, который будет ошибочным на величину x. Из рис.61, а следует очевидное равенство h = i1 + x - b (59) Помен
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.012 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 В действительности Земля неоднородна, массы внутри земной коры распределены неравномерно. В результате поверхность ее является весьма сложной. Поверхность, совпадающая с невозмущенной поверхностью морей и океанов и мысленно продолженная под материками при условии ее перпендикулярности силе тяжести, называется геоидом.
В действительности Земля неоднородна, массы внутри земной коры распределены неравномерно. В результате поверхность ее является весьма сложной. Поверхность, совпадающая с невозмущенной поверхностью морей и океанов и мысленно продолженная под материками при условии ее перпендикулярности силе тяжести, называется геоидом.


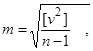



 В теодолите требуется выполнение условия перпендикулярности средней нити сетки к оси вращения теодолита (рис.5.14, а).
В теодолите требуется выполнение условия перпендикулярности средней нити сетки к оси вращения теодолита (рис.5.14, а). Углом наклона называется угол, образованный визирной осью с плоскостью горизонта. Углы наклона могут быть положительными и отрицательными (рис.5.18). Эти углы измеряются с помощью вертикального круга. Очевидно, что для измерения углов наклона необходимо фиксировать отсчетное устройство в горизонтальной плоскости, проходящей через центр круга, что достигается с помощью уровня при алидаде горизонтального круга. В некоторых теодолитах имеется специальный уровень при алидаде вертикального круга или устройство, компенсирующее ее наклон (теодолиты с компенсаторами). В теодолите 2Т30 вертикальный круг наглухо скреплен со зрительной трубой и вращается вместе с ней. По теории устройства теодолита после приведения его в рабочее положение нулевые штрихи вертикального круга и шкалы микроскопа должны совпадать при горизонтальном положении визирной оси. Фактически же нулевые штрихи могут не совпадать, что приводит к образованию угла, называемого "место нуля" (М0) (рис.5.19).
Углом наклона называется угол, образованный визирной осью с плоскостью горизонта. Углы наклона могут быть положительными и отрицательными (рис.5.18). Эти углы измеряются с помощью вертикального круга. Очевидно, что для измерения углов наклона необходимо фиксировать отсчетное устройство в горизонтальной плоскости, проходящей через центр круга, что достигается с помощью уровня при алидаде горизонтального круга. В некоторых теодолитах имеется специальный уровень при алидаде вертикального круга или устройство, компенсирующее ее наклон (теодолиты с компенсаторами). В теодолите 2Т30 вертикальный круг наглухо скреплен со зрительной трубой и вращается вместе с ней. По теории устройства теодолита после приведения его в рабочее положение нулевые штрихи вертикального круга и шкалы микроскопа должны совпадать при горизонтальном положении визирной оси. Фактически же нулевые штрихи могут не совпадать, что приводит к образованию угла, называемого "место нуля" (М0) (рис.5.19).
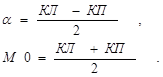
 Передатчик излучает электромагнитные волны, которые после отражения в точке В поступают в приемник, измеряющий время τ двойного пробега электромагнитной волной расстояния АВ. Расстояние D вычисляется по формуле
Передатчик излучает электромагнитные волны, которые после отражения в точке В поступают в приемник, измеряющий время τ двойного пробега электромагнитной волной расстояния АВ. Расстояние D вычисляется по формуле


 Круглый уровень в своей верхней части имеет вид сферической поверхности (рис.7.7, а). Пузырек уровня имеет вид лепёшки (вид сверху, рис.7.7, б).
Круглый уровень в своей верхней части имеет вид сферической поверхности (рис.7.7, а). Пузырек уровня имеет вид лепёшки (вид сверху, рис.7.7, б).
 рек цилиндрического уровня проходит через нуль-пункт. Поэтому круглый уровень в нивелире играет вспомогательную роль.
рек цилиндрического уровня проходит через нуль-пункт. Поэтому круглый уровень в нивелире играет вспомогательную роль.



