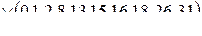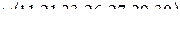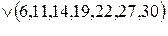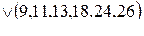Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №9 Минимизация логических функций с помощью карт КарноСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Карта Карно – это двумерная табличная форма представления булевой функции, позволяющая в графической наглядной форме легко отыскать минимальные ДНФ логических функций. Карта Карно, это преобразованная таблица истинности булевой функции. Карта содержит Минимизирующие карты обычно используют для ручной минимизации булевых функций при небольшом числе переменных. Правила минимизации следующие: 1. Две соседние клетки (два 0-куба) образуют один 1-куб. При этом клетки, лежащие на границах карты, также являются соседними по отношению друг к другу. 2. Четыре вершины могут объединяться, образуя 2-куб, содержащий две независимые координаты. 3. Восемь вершин могут объединяться, образуя один 3-куб. 4. Шестнадцать вершин, объединяясь, образуют один 4-куб и т.д. При числе переменных равном или большем пяти строят комбинированную карту, состоящую из совокупности четырехмерных (шестнадцатиклеточных) карт. Соседними клетками, в этом случае, являются клетки, совпадающие при совмещении карт поворотом вокруг общего ребра. Пример минимизации функции пяти аргументов приведен на рис. 1.
Рисунок 1 – Минимизация функции пяти переменных с помощью карты Карно
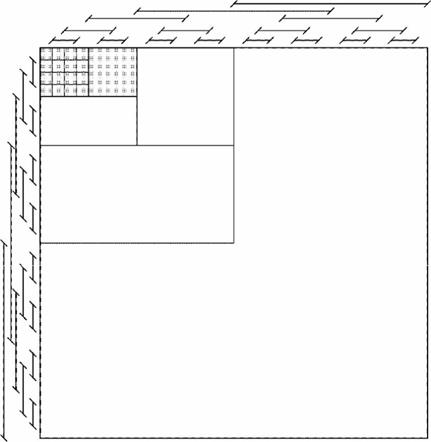
Следует отметить, что целесообразно выделять области максимально возможного размера (даже если эти области перекрываются) для более эффективной минимизации логического выражения. Карты Карно удобны для минимизации и не полностью определенных функций, которые будут рассмотрены ниже. Неопределенные значения можно заменить любыми – 0 или 1. Покрывая таблицу минимальным числом максимальных квадратов (или прямоугольников) со сторонами, равными степени двойки, так, чтобы они обязательно покрыли все единицы и не покрывали ни одного нуля, получим минимальную ДНФ всех возможных функций. Схема построения комбинированной карты при большом числе аргументов минимизируемой функции многократным отражением карты с шестнадцатью клетками показана на рис. 2.
Рисунок 2 – Построение карты Карно с помощью шестнадцатиклеточных карт
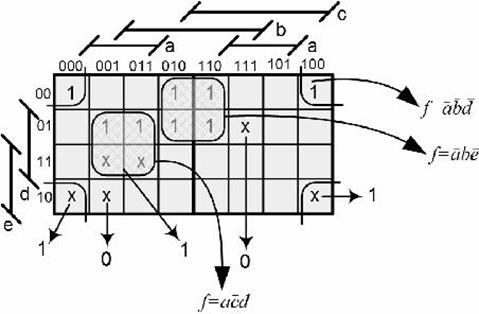
Особенную роль в процессе минимизации логических формул играют не полностью определенные или частичные функции, область определения которых меньше, чем полное множество наборов значений Главным свойством не полностью определенных функций является то, что, проводя минимизацию, можно произвольно доопределять функцию, подбирая такие ее значения на запрещенных наборах, которые позволяют произвести покрытие наилучшим образом. На рисунке 3 показан пример минимизации частичной функции, где х соответствует запрещенному набору. Произведенное доопределение необязательными нулями и необязательными единицами позволило провести дополнительную минимизацию в двух термах.
Рисунок 3 – Пример минимизации не полностью определенной функции Оборудование ПЭВМ IBMPC, операционная система Windows, OooWriter, MSWord. Задание на работу Доопределить оптимальным образом и минимизировать с помощью карты Карно частичные логические функции
7. Контрольные вопросы 1. Какая логическая функция называется частичной? 2. Сколько ячеек содержит карта Карно для функции семи переменных? 3. В чем заключается главная особенность минимизации не полностью определенных функций? 4. Какое количество клеток карты Карно допустимо объединять? Существуют ли какие-нибудь ограничения? 5. Какие клетки в карте Карно считаются соседними? 6. В чем состоит главный недостаток применения карт Карно для
Лабораторная работа №10 Минимизация логических функций методом Квайна‑Мак-Класки
Метод Квайна-Мак-Класки является одним из формальных методов минимизации логических выражений, реализующий достаточно простой алгоритм решения поставленной задачи. Исходную логическую функцию необходимо представить в совершенной дизъюнктивной нормальной форме (СДНФ), которая при расчетах заменяется кубическим комплексом C 0. Перед началом вычислений производится упорядочение этого комплекса по нормам векторов (весам наборов), при этом 0-кубы разбиваются на классы по количеству единиц в них. Конечной целью алгоритма является отыскание множества простых импликант, соответствующих минимизируемой функции, из которых затем выбирается некоторое подмножество, полностью покрывающее обязательные единицы исходной функции. Минимизация логического выражения осуществляется с использованием двух логических операций: склеивания и поглощения. Очевидно, что при группировании кубов в классы по количеству единиц в их наборах, склеивание возможно лишь между элементами соседних классов, поэтому такое упорядочение упрощает поиск соответствующих пар элементов. Все данные и промежуточные результаты заносятся в специальную таблицу, в которой фиксируются промежуточные этапы их обработки. На первом этапе первого цикла выполняются все возможные склеивания между 0-кубами. Результаты помещаются в продолжение таблицы. Затем производятся все поглощения 0-кубов 1-кубами. Если останутся 0-кубы, не поглощенные в результате второго этапа, им присваивается метка «первичная импликанта». На этом первый цикл склеивания и поглощения заканчивается. Второй цикл выполняется аналогично, но уже над комплексом Как только все циклы склеивания окончены, составляется таблица, строками которой являются первичные импликанты, а столбцами — исходные термы. Если в некоторый минитерм СДНФ входит какая-либо из первичных импликант, то на пересечении соответствующего столбца и строки ставится метка. Для полученной таблицы производится выбор минимального покрытия – такой совокупности первичных импликант, которая включает метки во всех столбцах, по крайней мере, по одной метке в каждом столбце. При нескольких возможных вариантах такого выбора предпочтение отдается варианту покрытия с минимальным суммарным числом букв в импликантах, образующих покрытие. Пример. Найти минимальную форму для функции Представим функцию в виде таблицы специального вида, произведя группировку 0-кубов по количеству входящих в них единиц (таблица 1). 0-куб из первого класса склеивается с 0-кубами из первого класса. Данная процедура повторяется для всех элементов из остальных смежных классов.
Таблица 1 Первичные импликанты
Затем производится поглощение 0-кубов 1-кубами (таблица 2). Сам процесс аналогичен поглощению 0-кубов. Таблица 2 Первичные импликанты С1
Аналогичная процедура повторяется для кубического комплекса Следует обратить внимание на то, что при обработке комплекса
Таблица 3 Первичные импликанты С2
В результате выполнения нескольких циклов получается искомая совокупность простых импликант. Для выбора минимально необходимой совокупности строится еще одна таблица (таблица 4). В данном случае импликанты из второй, четвертой, шестой и седьмой строк обеспечивают минимальное покрытие.
Таблица 4 Таблица покрытий
Ответ:
Оборудование ПЭВМ IBMPC, операционная система Windows, OooWriter, MSWord.
Задание на работу Минимизировать методом Квайна–Мак-Класки логические функции
7. Контрольные вопросы 1. В каком виде должна быть представлена функция для минимизации по методу Квайна-Мак-Класки? 2. Какова особенность минимизации n -кубов в методе Квайна-Мак-Класки? 3. Как в методе Квайна-Мак-Класки называются непоглощенные n -кубы? 4. Для чего в методе Квайна-Мак-Класки строится таблица покрытий? 5. По какому принципу производится выбор подмножества простых 6. В какой форме представляется результат минимизации по методу
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 972; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.241.191 (0.011 с.) |

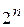 клеток, где
клеток, где 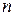 – число аргументов функции. Таким образом, каждому из наборов значений аргументов (СДНФ) соответствует одна клетка карты, и в эти клетки вписываются нули или единицы, представляющие значения функции на данном наборе.
– число аргументов функции. Таким образом, каждому из наборов значений аргументов (СДНФ) соответствует одна клетка карты, и в эти клетки вписываются нули или единицы, представляющие значения функции на данном наборе.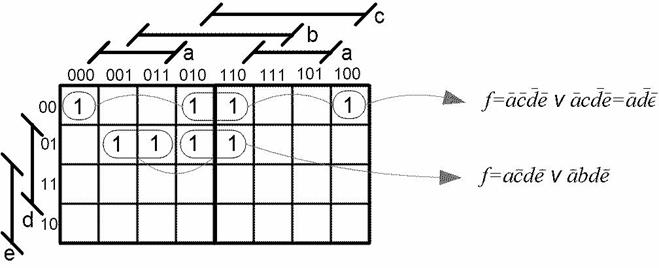
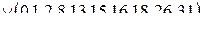
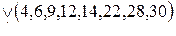
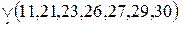
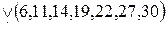
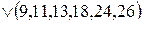
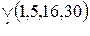
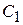 , составленным из 1-кубов. Циклы продолжаются до тех пор, пока это возможно.
, составленным из 1-кубов. Циклы продолжаются до тех пор, пока это возможно.
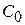
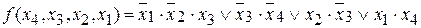 .
.