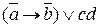Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная Работа №7 перевод чисел из одной позиционной системы счисления в другуюСодержание книги
Поиск на нашем сайте
Цель работы Познакомиться правилами перевода чисел из одной позиционной системы счисления в другую.
Порядок выполнения работы - ознакомится с теоретическими сведениями; - выполнить задание; - оформить отчет; - ответить на контрольные вопросы, заданные преподавателем.
Оформление отчета Отчет должен содержать: титульный лист, цель работы, описание пунктов выполнения лабораторной работы в соответствии с заданием, ответы на контрольные вопросы и выводы по работе. Теоретические сведения Система счисления – совокупность приемов и правил для записи чисел цифровыми знаками или символами. Способов записи чисел цифровыми знаками существует бесчисленное множество. Любая предназначенная для практического применения система счисления должна обеспечивать: · возможность представления любого числа в рассматриваемом диапазоне величин; · единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина); · простоту оперирования числами. Все системы представления чисел делят на позиционные и непозиционные.
где По этому принципу построены непозиционные системы счисления. Непозиционная система счисления– система, для которой значение символа не зависит от его положения в числе.
Существует и другой способ построения систем счисления: выбирается некоторое число
В этой записи значение каждой цифры зависит от того места, которое эта цифра занимает. Например, в числе 222 двойка участвует три раза. Но самая правая из них означает две единицы, вторая справа – два десятка, т. е. двадцать, а третья – две сотни. В данном примере имеется в виду десятичная система. Если бы мы пользовались какой-либо другой системой счисления, скажем с основанием В процессе преобразования информации в ЭВМ возникает необходимость перевода чисел из одной позиционной системы счисления в другую.
Для позиционной системы счисления справедливо равенство:
или
где На практике используют сокращенную запись чисел:
Целое число
Числа в разных системах счисления можно представить следующим образом:
В общем виде задачу перевода числа из системы счисления с основанием
Оборудование ПЭВМ IBMPC, операционная система Windows, OOoWriter, MSWord. Задание на работу Перевести число из одной позиционной системы счисления в другую в соответствии с вариантом.
7. Контрольные вопросы
1. Какая система называется позиционной? Приведите примеры таких систем. 2. Какая система называется непозиционной? Приведите примеры таких систем. 3. Правила какой арифметики используются при переводе числа из одной системы счисления в другую делением на основание новой системы?
Лабораторная работа №8 Преобразование выражений булевой алгебры
Цель работы Изучить методы преобразования выражений булевой алгебры.
Порядок выполнения работы - ознакомится с теоретическими сведениями; - выполнить задание; - оформить отчет; - ответить на контрольные вопросы, заданные преподавателем.
Оформление отчета Отчет должен содержать: титульный лист, цель работы, описание пунктов выполнения лабораторной работы в соответствии с заданием, ответы на контрольные вопросы и выводы по работе.
Теоретические сведения Булевой алгеброй называется непустое множество A с двумя бинарными операциями Ù или × (аналог конъюнкции), Ú (аналог дизъюнкции), унарной операцией Ø (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:
1. Ассоциативность (сочетательный закон):
2. Коммутативность (переместительный закон):
3. Законы поглощения:
4. Законы склеивания:
5. Дистрибутивность (распределительный закон):
6. Дополнительность:
7. Идемпотентность:
8. Закон де Моргана:
9. Аннулирующее свойство единицы:
10. Свойство нуля:
11. Свойства инверсии (инволютивность):
12. Правило вычеркивания:
Преобразование в дизъюнктивную нормальную форму. Всякая аналитическая запись функции может быть преобразована в нормальную форму. Систематическая процедура преобразования функции в нормальную форму с использованием свойств двоичных функций может быть описана следующим образом: Шаг 1. Если в функции имеются операции, отличные от И, ИЛИ, НЕ, то используем следующие свойства для их устранения:
Шаг 2. Используем свойства инверсии и законы де Моргана чтобы каждая операция отрицания относилась только к одной переменной. Шаг 3. Используем свойства дистрибутивности и другие свойства, чтобы получить нормальную форму. Например, преобразовать в нормальную дизъюнктивную форму функцию
Способы преобразования НФ в СНФ. Совершенная нормальная форма отличается от нормальной формы (НФ) тем, что всегда содержит термы только максимального ранга и дает однозначное представление функции. Произвольная нормальная дизъюнктивная форма (НДФ) переводится в СНДФ следующим образом. Пусть
Произвольная НКФ переводится в СКНФ путем следующего преобразования: Пусть
Переведем в СДНФ функцию из предыдущего примера:
Преобразование в СКНФ выражения произвольного вида. Процесс преобразования функции осуществляется для исходной функции, представленной таблицей истинности в соответствии с выражением:
где
Например, представить функцию
В соответствии с данной таблицей функция
Оборудование ПЭВМ IBMPC, операционная система Windows, OooWriter, MSWord. Задание на работу Приведенные логические выражения: · преобразовать в СДНФ; · преобразовать в СКНФ; · преобразовать в базис «И-ИЛИ-НЕ» и минимизировать.
7. Контрольные вопросы 1. В чем отличие булевой алгебры от алгебры логики? 2. Чем отличаются совершенная нормальная и нормальная формы представления функций? 3. Перечислите способы представления функций булевой алгебры. 4. Какие операции составляют базис булевой алгебры? Является ли эта алгебра полной? 5. Какое высказывание называется абсолютно истинным? 6. Какие значения может принимать булева переменная?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.18.97 (0.011 с.) |

 ,
, – запись числа
– запись числа  в системе счисления
в системе счисления  .
. – основание системы счисления, и каждое число
– основание системы счисления, и каждое число  представляется в виде комбинации его степеней с коэффициентами, принимающими значения от 0 до
представляется в виде комбинации его степеней с коэффициентами, принимающими значения от 0 до  , т. е. в виде:
, т. е. в виде:
 и
и  . Системы счисления, построенные, таким образом, называются позиционными.
. Системы счисления, построенные, таким образом, называются позиционными. ,
, ,
, – произвольное число, записанное в системе счисления с основанием
– произвольное число, записанное в системе счисления с основанием  – количество целых и дробных разрядов.
– количество целых и дробных разрядов.
 .
.
 в систему счисления с основанием
в систему счисления с основанием  можно представить как задачу определения коэффициентов
можно представить как задачу определения коэффициентов 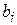 нового ряда, изображающего число в системе с основанием
нового ряда, изображающего число в системе с основанием  -арифметики, т.е. по правилам исходной системы счисления.
-арифметики, т.е. по правилам исходной системы счисления.









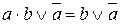

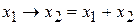

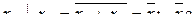



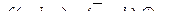 .
.







 . Тогда:
. Тогда:
 .
. . Тогда:
. Тогда: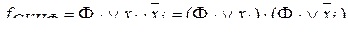
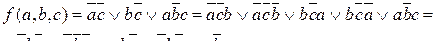
 (1)
(1)
 в виде СКНФ. Таблица истинности для данной функции имеет вид:
в виде СКНФ. Таблица истинности для данной функции имеет вид:
 .
.