Лабораторная Работа №11 методы эффективного кодирования информации

 

Цель работы

Изучить алгоритм Хаффмена для оптимального префиксного кодирования алфавита с минимальной избыточностью.

 

Порядок выполнения работы

- ознакомится с теоретическими сведениями;

- выполнить задание;

- оформить отчет;

- ответить на контрольные вопросы, заданные преподавателем.

 

Оформление отчета

Отчет должен содержать: титульный лист, цель работы, описание пунктов выполнения лабораторной работы в соответствии с заданием, ответы на контрольные вопросы и выводы по работе.

 

Теоретические сведения

Алгоритм Хаффмена (англ. Huffman) – алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью был разработан в 1952 году доктором Массачусетского технологического института Дэвидом Хаффменом. Он более практичен и никогда по степени сжатия не уступает методу Шеннона-Фэно, более того, он сжимает максимально плотно.

Этот метод кодирования состоит из двух основных этапов:

Построение оптимального кодового дерева.

Построение отображения код-символ на основе построенного дерева.

Алгоритм кодирования может быть представлен следующим образом:

Символы первичного алфавита m1 выписывают в порядке убывания вероятностей.

Последние n0 символов объединяют в новый символ, вероятность которого равна сумме этих символов, удаляют эти символы и вставляют новый символ в список остальных на соответствующее место (по вероятности). n0 вычисляется из системы:

 

где a – целое число, m1 и m2 – мощность первичного и вторичного
алфавита соответственно.

Последние m2 символов снова объединяют в один и вставляют его в соответствующей позиции, предварительно удалив символы, вошедшие в объединение.

Предыдущий шаг повторяют до тех пор, пока сумма всех m2 символов не станет равной 1.

Этот процесс можно представить как построение дерева, корень которого – символ с вероятностью 1, получившийся при объединении символов из последнего шага, его m2 потомков — символы из предыдущего шага и т.д.

Каждые m2 элементов, стоящих на одном уровне, нумеруются от 0 до m2-1. Коды получаются из путей (от первого потомка корня и до листка). При декодировании можно использовать то же самое дерево, считывается по одной цифре и делается шаг по дереву, пока не достигается лист – тогда выводится символ, стоящий в листе и производится возврат в корень. Для двоичного кода описанная методика значительно упрощается. В этом случае n0=m2=2, а полученное в результате построения дерево называется двоичным. Рассмотрим применение алгоритма Хаффмена для последовательности «aa bbb cccc ddddd» (таблица 1, таблица 2).

Энтропия исходного сообщения равна:

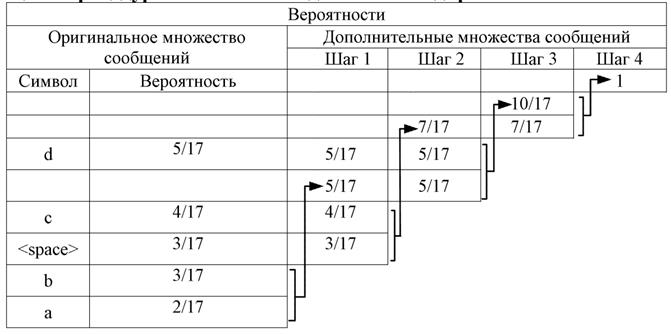
Таблица 1. Процедура оптимального двоичного кодирования

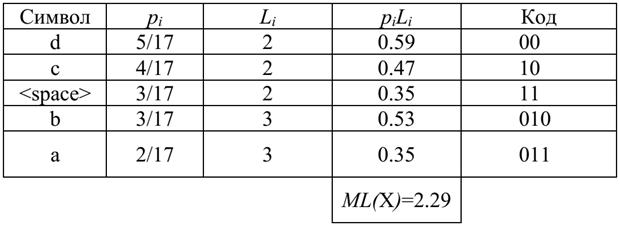
Таблица 2. Результат кодирования по методу Хаффмена

Отметим, что в ряде случаев вместо таблицы, отражающей процедуру
кодирования по методу Хаффмена, удобнее работать со списком букв и
весами:

d₅ c₄ <space>₃ b₃ a₂,

осуществляя с помощью скобок группировку символов. Например, первый
шаг может быть представлен следующим образом:

d₅ (b₃ + a₂)₅ c₄ <space>₃

(c₄ + <space>₃)₇ d₅ (b₃ + a₂)₅

[d₅ + (b₃ + a₂)₅]₁₀ + (c₄ + <space>₃)₇

 

Полученные соотношения удобно представлять в виде дерева, по которому можно составить код для каждого символа (рис. 1).

Рисунок 1 – Кодовое дерево

 

Средняя длина сообщения, кодирующего заданную последовательность, равна:

Оборудование

ПЭВМ IBMPC, операционная система Windows, OooWriter, MSWord.

 

Задание на работу

Построить кодовое дерево и код Хаффмена для последовательности
символов в соответствии с вариантом (таблица 3).

Таблица 3. Варианты заданий на работу

Вариант	Текст
1	one important method of transmitting messages
2	transmit in their place sequences of symbols.
3	there are more messages which might be sent t
4	there are kinds of symbols available, then so
5	the messages must use more than one symbol. I
6	is assumed that each symbol requires the same

 

Подсчитайте энтропию исходного сообщения и среднюю длину кодирующего сообщения.

 

7. Контрольные вопросы

1. Какова суммарная вероятность всех символов, участвующих в кодировании по методу Хаффмена?

2. Сколько раз кодеру Хаффмена необходимо просматривать сжимаемый текст для получения окончательного результата?

3. Может ли среднее количество бит на единицу сообщения для кодирования по методу Хаффмена быть меньше энтропии сообщения? Почему?

4. Нужно ли при кодировании по методу Хаффмена кроме сжатого сообщения передавать какую-либо дополнительную информацию? Поясните ответ.

5. Какой вариант сжатия – обратимое или необратимое – реализует алгоритм Хаффмена?

6. Почему кодирование по Хаффмену называется префиксным?