
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декодирование последовательности по алгоритму Витерби
По характеру использования информации, поступающей на вход декодера, алгоритмы декодирования делятся на несколько групп. К алгебраическим относятся алгоритмы, работа которых основана на использовании алгебраических свойств кодовых слов. При этом в демодуляторе производится жесткое решение о принятых сигналах и на вход декодера поступают дискретные символы, алфавит которых совпадает с алфавитом на передаче. При вероятностном декодировании существенным является более полное использование информации с выхода канала. В этом случае в демодуляторе производится мягкое решение, содержащее информацию об апостериорной вероятности принимаемых символов. Из вероятностных алгоритмов наиболее разработаны алгоритм последовательного декодирования и алгоритм максимального правдоподобия, предложенный А. Витерби. Алгоритм имеет ряд преимуществ перед другими и его широко используют для декодирования коротких СК. Рассмотрим алгоритм на примере кода со скоростью R = 1/ п. Декодирование состоит в прослеживании по кодовой решетке пути с максимальной апостериорной вероятностью. Декодированный путь можно указать одним из способов: набором оценок кодовых ветвей
Р (
При декодировании по критерию (11), выбирают такую последовательность ветвей
МП =
называемая метрикой декодированного пути. Метрика пути содержит в качестве слагаемых метрики ветвей: МП = Периодическая структура решетчатой диаграммы существенно упрощает сравнение и выбор путей в соответствии с правилами (12). Число состояний на решетке ограничено, и два наугад выбранных достаточно длинных пути имеют, как правило, общие состояния. Отрезки путей, входящих в эти состояния, необходимо сравнить и выбрать путь с наименьшей метрикой. Такой путь называют выжившим. В соответствии с алгоритмом Витерби сравнение и отбрасывание отрезков путей производится периодически на каждом шаге декодирования. Рассмотрим декодирование кода (7, 5), символы которого передаются по дискретному каналу. В этом случае метрика ветви MB равна расстоянию Хэмминга между набором символов z (1) z (2) на входе декодера и набором символов v (1) v (2), соответствующих данной ветви на решетчатой диаграмме. Если z (1) z (2) = 01, то возможные значения MB для кода (7, 5) с решеткой, изображенной на рис. 3, будут: MB(00) = 1, MB(01) = = 0, MB(11) = 1 и MB(10) = 2. Метрика пути есть сумма метрик ветвей, образующих некоторый путь на решетчатой диаграмме. Путь конечной длины оканчивается в определенном состоянии. Метрика состояния МС равна МП, который заканчивается в данном состоянии. Шаг декодирования состоит в обработке декодером принимаемых из канала данных в интервале между двумя соседними уровнями узлов. На рис. 6 показано развитие процесса декодирования символов кода (7, 5). На вход декодера поступают пары символов из канала z (1) z (2) = 11 10 00 11 01... Цифрами около ветвей обозначены метрики ветвей, цифры в кружках обозначают метрики состояний. В начальный момент времени полагаем, что декодер находится в состоянии 00 и исходная метрика МС (00) = 0. Если из канала поступили символы 11, то метрики двух ветвей, выходящих из этого состояния, MB (00) = 2 и MB (11) = 0. Это отмечено на первом шаге декодирования. Так как других ветвей из состояния 00 в состояния 00 и 11 нет, то метрики этих состояний принимают равными метрикам входящих ветвей: МС (00) = 2 и МС (10) = 0. Аналогично и на следующем шаге, когда из канала поступают символы 10. Здесь MB (00) = 1, MB (11) = 1и MB (10) = 0, MB (01) = 2. Метрики состояний на этом шаге определяются теперь как суммы метрик входящих ветвей с метриками предыдущих состояний: МС (00) = 2 + 1 = 3, МС (10) = 2 + 1 = 3, МС (01) = 0 + 0 = 0, МС (11) = 0 + 2 = 2. На этом развитие решетчатой диаграммы заканчивается.
Рисунок 6
К каждому новому состоянию ведет два пути. К примеру, к состоянию 00 ведут пути из состояний 00 и 01. Декодер вычисляет метрики путей как суммы метрик предыдущих состояний и метрик входящих ветвей. Далее производят попарное сравнение метрик путей, входящих в каждое состояние. В результате сравнения выбирают меньшую метрику и ее считают метрикой данного состояния для последующего шага декодирования. Путь, входящий в данное состояние с меньшей метрикой, считают выжившим. Пути, входящие в состояния с большими метриками, считают оборванными. Они показаны на решетчатой диаграмме штриховыми линиями. Таким образом, на каждом шаге декодирования в соответствии с алгоритмом Витерби в каждом из состояний решетчатой диаграммы производятся однотипные операции: 1) сложение метрик предыдущих состояний с метриками соответствующих ветвей; 2) сравнение метрик входящих путей 3) выбор путей с наименьшими метриками, величины которых используют как метрики состояний на последующем шаге декодирования (сокращенно ССВ). Если метрики сравниваемых путей одинаковы, выбор одного из двух путей производят случайным образом. На каждом шаге в результате сравнения половина возможных путей отбрасывается и в дальнейшем не используется. Другая половина образует продолжения путей для следующего шага декодирования. Из каждого состояния на следующем шаге вновь появляются два варианта продолжения путей. Это обеспечивает постоянство вычислений, производимых на каждом шаге. Декодер прослеживает по кодовой решетке путь, имеющий минимальное расстояние от пути, который генерирует кодер.
Построим решетчатую диаграмму состояний, внося двукратную ошибку на 3 и 2 ходу, согласно варианту: V2= 1 0. 0 0.11.00.11.10.11.11.10.00.01.01.00.01.01.00.10.11.11.10.11.11.10.11.11.10.11.00.11.10.00.01.01.11.11.10.11.00.00.00.00
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.193.223 (0.006 с.) |
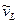 , составляющих путь; последовательностью оценок состояний кодера
, составляющих путь; последовательностью оценок состояний кодера  либо последовательностью оценок информационных символов на входе кодера
либо последовательностью оценок информационных символов на входе кодера  . Поступающая на вход декодера последовательность
. Поступающая на вход декодера последовательность  будет декодирована с минимальной вероятностью ошибки, если из всех возможных путей выбрать оценку
будет декодирована с минимальной вероятностью ошибки, если из всех возможных путей выбрать оценку  , для которой максимальна апостериорная вероятность
, для которой максимальна апостериорная вероятность , (12)
, (12)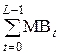 , где метрики ветвей
, где метрики ветвей 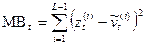 . В дискретном канале для оценки расстояний используют метрику Хэмминга.
. В дискретном канале для оценки расстояний используют метрику Хэмминга.



