
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алфавитное и равномерное кодирование.Содержание книги
Поиск на нашем сайте ДИСКРЕТНАЯ МАТЕМАТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным и самостоятельной работам
для студентов специальности «Системы и методы принятия решений» дневной формы обучения
Краматорск 2011
Лабораторная работа №1
Алфавитное и равномерное кодирование. (Алгоритмы Фано и Хаффмана). Цель работы: изучить алгоритмы кодирования информации посредством методов Фано и Хаффмена.
Задание. 1. Для заданных распределений вероятностей появления букв построить заданный код и рассчитать среднюю длину кодирования.
2. Написать программу, которая осуществляет кодирование Вашей фамилии, имени и отчества методом Фано или Хаффмена в зависимости от варианта.
Лабораторная работа №2 Самокорректирующиеся коды. Коды Хемминга. Цель работы: изучение общих методов формирования кодов, получение практических навыков по формированию корректирующих кодов на примере построения и декодирования систематического кода и изучение его свойств. Задание. Обнаружить и исправить ошибку в представленном коде, декодировать сообщение.
Краткие теоретические сведения. Каждое слово сообщения A при равномерном кодировании допускает разложение вида A =Ai1,Ai2 ,Ai3,…Ain, и имеет единственное такое разложение. Если ограничиться бинарным кодированием, то Ai = a1 a2 a3…..am номера слов в словаре, записанные в двоичной системе (ai принимает значения 0 или1). Необходимо отметить, что каждый двоичный номер слова может быть однозначно записан и десятеричным числом. Пусть S”(I) – подмножество всех слов, допускающих разложение указанного вида. Рассмотрим следующую схему кодирования: A1® B1 A2® B2 A3® B3 (2.1) …. As® Bs, где Bi = b1 b2 b3 …bl – элементарные двоичные коды, имеющие одинаковую длину l = m + k, при этом такие, чтобы по коду, полученному на выходе канала связи (помеха может изменить 0 на 1 или наоборот, но не может добавить или убрать элемент bi) однозначно восстановить код на входе канала и из него получить исходное сообщение.
Построение самокорректирующихся кодов было осуществлено Хеммингом. Рассмотрим случай, когда источник помех может внести не более одного инвертирования в элементарный код Bi (р =1). Вариантов получения элементарного кода Bi будет l +1 (правильный и l штук с инвертированием bi на каждой позиции). Для того, чтобы дополнительных разрядов в коде Bi хватило для кодирования l +1 случаев, необходимо выполнение следующего условия: 2 m ≤ 2 l / (l + 1) (2.2) Из этих соображений выбираем l как наименьшее целое число, удовлетворяющее неравенству (2). Дальнейшее построение будет состоять из трех этапов: 1. Построение кодов Хемминга (описание алгоритма кодирования). 2. Обнаружение ошибок в кодах Хемминга. 3. Декодирование.
Построение кодов Хемминга (описание алгоритма кодирования) В множестве натуральных чисел {1,2,3,…, l }выделим следующие подмножества: 1, 3, 5, 7, 9 ….(содержатся все числа, у которых при переводе в двоичную запись в последнем разряде 1); 2, 3, 6, 7, 10 ….(содержатся все числа, у которых при переводе в двоичную запись в предпоследнем разряде 1); .......... 2k–1, 2k–1 +1, ….(содержатся все числа, у которых при переводе в двоичную запись в k –ом, считая справа, разряде 1). Наименьшие члены этих подмножеств являются степенями 2: 1 = 20; 2 = 21; 4 = 22;…., причем 2k–1 ≤ l, а 2k+1 ³ l +1. Члены bi набора b1 b2 b3 …bl, у которых индекс i принадлежит множеству {1, 2, 4,… 2k–1}, называются контрольными членами, остальные – информационными. Таким образом, контрольных членов будет k, а информационных l – k = m. Сформулируем правило построения набора …bl по набору a1 a2 a3…..am. Сначала определяются информационные члены: b3 = a1 b5 = a2 b6 = a3 ..... Таким образом, набор информационных членов, расположенных в естественном порядке, совпадает с набором a1 a2 a3…..am. Затем определяются контрольные члены, b1 = b3+ b5 + b7 + … (mod 2), b2 = b3+ b6 + b7 + … (mod 2), (2.3) b4= b3+ b6 + b7 + … (mod 2), .............
значения которых 0 или 1 и помещаются на соответствующих местах в элементарных кодах Bi. По сути, создается кодовый словарь для схемы кодирования (1), в котором для каждого элементарного кода выполняются следующие условия (суммирование по mod 2): b1 + b3+ b5 + b7 +…= 0, b2 + b3+ b6 + b7 + … = 0, (2.4) b4 + b3+ b6 + b7 + … = 0, ............. (количество единиц в позициях элементарного кода, определяемых индексами, четно).
Обнаружение ошибок в кодах Хемминга Ошибка на выходе из канала связи может быть обнаружена и исправлена так (для построенного кода – не больше одной в каждом элементарном коде). Номер позиции S (записанный в двоичной системе), в которой произошла ошибка, определяется так: S = Sk… S2 S1 , где Si определяется по формулам (4) для элементарного кода, полученного на выходе канала связи. Если ошибки нет, то Si = 0 и общий результат S = 0.
Пример 1: Пусть на вход канала связи поступил элементарный код 0110011 (т.е закодировано **1*011 (поз. 3,5,6,7– информационные, а контрольные члены заменены *)). На выходе получено 0110001 (искажен 6–й член элементарного кода). Вычислим S. S1 = b1 + b3+ b5 + b7 = 0 + 1 + 0 + 1 = 0 (mod 2), S2 = b2 + b3+ b6 + b7 = 1 + 1 + 0 + 1 = 1 (mod 2), S3 = b4 + b5 + b6 + b7 = 0 + 0 + 0 + 1 = 1 (mod 2). S = 1 1 0 = 6 (в десятичной системе). Пример 2: Пусть на выходе получено 0111011 (искажен 4–й (контрольный) член элементарного кода). S1 = b1 + b3+ b5 + b7 = 0 + 1 + 0 + 1 = 0 (mod 2), S2 = b2 + b3+ b6 + b7 = 1 + 1 + 1 + 1 = 0 (mod 2), S3 = b4+ b5 + b6 + b7 = 1 + 0 + 1 + 1 = 1 (mod 2). S = S3 S2 S1= 1 0 0 = 4 (в десятичной системе). Тогда восстановленное сообщение имеет вид: 0110011, а исходное сообщение – 1011 (удалены контрольные члены, выделенные цветом) Декодирование После получения закодированного сообщения происходит его разбивка на элементарные коды, вычисление для каждого кода S и в случае его неравенства 0 – корректировка соответствующего информационного члена (если S указывает на контрольный член, то корректировка не нужна). После удаления всех контрольных членов получаем исходное сообщение.
Примечание: Рассмотрено построение кодов Хемминга для бинарного кодирования и допустимом числе ошибок в элементарных кодах не более одной. Существует теория для построения таких кодов для равномерного кодирования любой арности и числе ошибок не более 2, 3,… и. д. Лабораторная работа №3 Формальные грамматики и языки|речь|. (Цепочки. Классификация грамматик по Хомскому).
Цель работы: закрепить понятия « алфавит», «цепочка», «формальная грамматика» и «формальный язык», «выводимость цепочек», «эквивалентная грамматика»;сформировать умения и навыки распознавания типов формальных языков и грамматик по классификации Хомского, построения эквивалентных грамматик.
Задание. 1.Определить к какому типу по Хомскому относится данная грамматика, какой язык она порождает, каков тип языка. 2.Указать максимально возможный номер типа грамматики и языка.
Тип 0 Любая порождающая грамматика является грамматикой типа 0. На вид правил грамматик этого типа не накладывается никаких дополнительных ограничений. Класс языков типа 0 совпадает с классом рекурсивно перечислимых языков. Тип 1 Грамматика G = 〈 T, N, P, S 〉 называется неукорачивающей, если правая часть каждого правила из P не короче левой части (т. е. для любого правила α → β правил. Грамматикой типа 1 будем называть неукорачивающую грамматику. Тип 1 в некоторых источниках определяют с помощью так называемых контекстно-зависимых грамматик. Грамматика G = 〈 T, N, P, S 〉 называется контекстно-зависимой (КЗ), если каждое правило из P имеет вид α → β, где α = ξ1 A ξ2, β = ξ1γξ2, A В виде исключения в КЗ-грамматике допускается наличие правила с пустой правой частью S → l, при условии, что S (начальный символ) не встречается в правых частях правил. Цепочку ξ1 называют левым контекстом, цепочку ξ2 называют правым контекстом. Язык, порождаемый контекстно-зависимой грамматикой, называется контекстно- зависимым языком. Тип 2 Грамматика G = 〈 T, N, P, S 〉 называется контекстно-свободной (КС), если каждое правило из Р имеет вид A → β, где A Грамматикой типа 2 будем называть контекстно-свободную грамматику. КС-грамматика может являться неукорачивающей, т.е. удовлетворять ограничениям неукорачивающей грамматики. Тип 3 Грамматика G = 〈 T, N, P, S 〉 называется праволинейной, если каждое правило из Р имеет вид A → wB либо A → w, где A, B Грамматика G = 〈 T, N, P, S 〉 называется леволинейной, если каждое правило из Р имеет вид A → Bw либо A → w, где A, B Леволинейные и праволинейные грамматики определяют один и тот же класс языков. Такие языки называются регулярными. Право- и леволинейные грамматики также будем называть регулярными. Регулярная грамматика является грамматикой типа 3. Автоматной грамматикой называется праволинейная (леволинейная) грамматика, такая, что каждое правило с непустой правой частью имеет вид: A → a либо A → aB (для леволинейной, соответственно, A → a либо A → Ba), где A, B
Лабораторная работа №4 Построение разных|различных| типов конечных автоматов (Детерминированные и недетерминированные конечные автоматы).
Цель работы: изучить основные понятия конечных автоматов, научиться преобразовывать недетерминированный конечный автомат в эквивалентный ему детерминированный конечный автомат.
Задание По недетерминированному конечному автомату, диаграмма которого представлена в индивидуальном задании, построить детерминированный конечный автомат, распознающий тот же язык. В ходе выполнения задания должны быть выполнены и описаны следующие подзадачи:
1. Записать параметры заданного НКА в виде: К *={ Q, A, q 0, g*, F }, (4.1)
где А ={ а 1, а 2,..., аn } – входной алфавит; Q ={ q 0, q 1, q 2,..., qm } – множество состояний автомата; q 0 – начальное состояние автомата, q 0Î Q; g* – функция переходов недетерминированного конечного автомата, является отображением типа Q x А ®[2 Q \Æ]. Напомним, что для любого множества М через 2 М обозначается множество всех подмножеств из М; символ Æ обозначает пустое множество. Совокупность g *(qi,аj) – это всегда непустое подмножество состояний автомата, в любое из которых он может перейти из состояния qi под воздействием буквы аj, здесь qi Î Q, аj Î А. F –множество допускающих состояний, F Í Q.
2. Построить таблицу переходов для заданного НКА 3. Преобразовать НКА в КА. 4.Проверить состояния полученного КА на достижимость и эквивалентность 5. Записать параметры заданного КА в виде: К ={ Q, A, q 0, g, F }, (4.2)
где А ={ а 1, а 2,..., аn } – входной алфавит; Q ={ q 0, q 1, q 2,..., qm } – множество состояний автомата; q 0 – начальное состояние автомата, q 0Î Q; g – функция переходов конечного автомата, представляющая собой отображение типа Q x А ® Q (если g (qi,аj)= qk, то автомат из состояния qi под воздействием буквы аj должен перейти в состояние qk); F – множество допускающих состояний, F Í Q.
6. Построить диаграмму состояний полученного КА. 7. Проверить, допускает ли полученный КА цепочки, которые были допущены НКА. 8. Составить программу, реализующую работу полученного КА. Индивидуальные задания
Лабораторная работа №5 Задание Разработать программное средство, реализующее следующие функции: а) ввод произвольной формальной грамматики и проверка ее на принадлежность к классу КС-грамматик; б) построение МП-автомата по КС-грамматике; Продемонстрировать разбор некоторой входной строки с помощью по- строенного автомата для случаев: а) входная строка принадлежит языку исходной КС-грамматики и допускается МП-автоматом; б) входная строка не принадлежит языку исходной КС-грамматики и не принимается МП-автоматом. Индивидуальные варианты заданий представлены в таблице 5.1.
Таблица 5.1 - Варианты заданий для лабораторной работы №5
ДИСКРЕТНАЯ МАТЕМАТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным и самостоятельной работам
для студентов специальности «Системы и методы принятия решений» дневной формы обучения
Краматорск 2011
Лабораторная работа №1
Алфавитное и равномерное кодирование. (Алгоритмы Фано и Хаффмана). Цель работы: изучить алгоритмы кодирования информации посредством методов Фано и Хаффмена.
Задание. 1. Для заданных распределений вероятностей появления букв построить заданный код и рассчитать среднюю длину кодирования.
2. Написать программу, которая осуществляет кодирование Вашей фамилии, имени и отчества методом Фано или Хаффмена в зависимости от варианта.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.014 с.) |



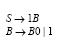





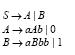









 P выполняется неравенство | α | ≤ | β |). В виде исключения в неукорачивающей грамматике допускается наличие правила S → l, при условии, что S (начальный символ, аксиома) не встречается в правых частях
P выполняется неравенство | α | ≤ | β |). В виде исключения в неукорачивающей грамматике допускается наличие правила S → l, при условии, что S (начальный символ, аксиома) не встречается в правых частях N)+, ξ1, ξ2
N)+, ξ1, ξ2  Вариант 1
Вариант 1
 Вариант 2
Вариант 2
 Вариант 3
Вариант 3
 Вариант 4
Вариант 4
 Вариант 5
Вариант 5
 Вариант 6
Вариант 6
 Вариант 7
Вариант 7
 Вариант 8
Вариант 8
 Вариант 9
Вариант 9
 Вариант 10
Вариант 10
 Вариант 11
Вариант 11
 Вариант 12
Вариант 12
 Вариант 13
Вариант 13
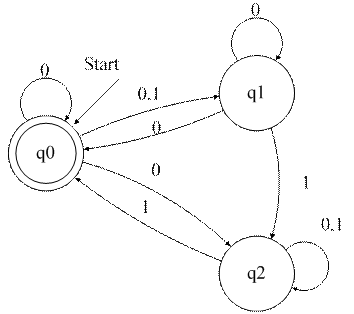 Вариант 14
Вариант 14
 Вариант 15
Вариант 15
 Вариант 16
Вариант 16
 Вариант 17
Вариант 17
 Вариант 18
Вариант 18
 Вариант 19
Вариант 19
 Вариант 20
Вариант 20



