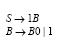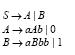Самокорректирующиеся коды. Коды Хемминга.

Цель работы: изучение общих методов формирования кодов, получение практических навыков по формированию корректирующих кодов на примере построения и декодирования систематического кода и изучение его свойств.

Задание.

Обнаружить и исправить ошибку в представленном коде, декодировать сообщение.

Вариант	Закодированное сообщение
	1 1 1 0 1 0- 0 1 0 1 0 0 0 0 0-0 1 0 0 1 1 1-1 1 0 1 0 1 1 1 1- 0 0 0 0 0 1
	1 0 1 0 0 1 1-0 0 0 1 1 1 0-1 1 1 0 1 0-1 0 0 0 0 0 1-1 1 0 0 1 0 0 0 0-1 1 0 0 1 1 0 0 1- -0 1 0 1 1 0 0 0 1 0-1 1 0 1 0 1 1 1 1-0 0 1 0 0 0
	1 1 1 1 1 1 1 0 1-1 0 0 0 1 0 1-0 1 0 0 1 0 0 1 1-1 1 1 0 0 1 1 1 1 1-0 0 1 0 0 0 0 1 1 0 1 1 1 0 0-1 1 1 0 0 1-0 1 1 0 1 0 1-0 0 0 0 0 1
	0 1 0 0 0 1 0 1 1-0 1 1 0 0 1 1 0 1-0 1 0 1 1 1 1 1 1-1 0 1 0 0 0 1 0 1 1-0 0 1 0 0 1 0 1 1 1 0 1 0-0 0 0 0 0 1-0 1 1 1 0 1 0 0 0-0 0 0 0 1 0-1 0 1 1 0 1 1-0 1 1 0 1 1 0 1 1- 1 1 1 0 0 1-1 0 1 0 0 1 1-0 0 1 0 0 0
	1 0 1 1 1 1 0-1 0 1 0 1 0 0-0 0 1 0 1 1 1-1 0 1 1 0 0 0-1 0 1 1 1 0 0 0 0-1 1 0 0 0 0- 0 0 0 1 1 1 0-1 1 1 0 0 1-0 1 0 1 0 1 1 0 0 -1 0 0 0 1 1 1-1 0 0 1 1 0 1 0 0-0 0 0 0 1 0
	0 1 0 1 0 1 0 0 1-0 0 0 1 0 1 1-0 0 1 0 1 1 1-0 0 1 0 0 0-1 0 0 0 0 0 1-0 0 0 0 1 0
	1 0 0 1 0 1 0-0 1 0 0 0 0 1-0 1 1 1 1 0 0 0 0 1-0 1 0 0 1 1 1-1 0 1 0 0 1 1 0 0 1- 0 0 1 0 1 1 1-1 1 1 0 1 0-0 0 0 0 0 1
	1 0 1 1 0 1 1-1 0 1 0 1 1 1-0 1 1 0 1 0 1-1 1 0 1 0 1 0 1 0-1 1 1 0 0 1-1 0 0 0 1 1 1- 0 0 0 0 0 1
	0 0 1 1 1 1 0 1 0 1-0 0 0 1 1 0 0 1 0 0-0 0 1 1 1 1 1-1 1 1 0 1 0-0 0 1 0 0 1 0 1 0 1 1 1 0 0 0 1 1 1-0 1 0 0 1 1 1-0 1 0 1 0 1 0 0 1-0 0 0 0 1 0
	1 0 0 1 0 1 0-1 0 1 0 0 0 1-1 0 0 0 0 0 1-1 1 1 1 1 0 0 1 1 1-1 0 1 0 0 1 1- 0 0 0 1 0 1 1-0 0 1 1 1 0 0 1 1 1-1 0 0 1 0 0 0 0 0-1 1 1 0 0 1-0 0 0 1 1 0 1 1 1 0- 0 0 1 0 0 0
	0 1 1 0 1 0 1-1 0 1 1 0 0 0-0 1 1 1 1 1 0 1 1-0 0 0 1 1 1 0-0 1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1-0 0 1 1 1 1 1-1 0 0 1 1 1 0 0 0-0 0 1 0 0 0
	0 1 1 0 1 1 1 0 0-0 0 1 0 0 0-1 1 1 1 0 1 1 0 0-1 0 1 0 1 1 1-0 1 0 0 0 1 0 1 1- 0 1 1 1 1 0 0 1 1 1 0-0 0 1 1 1 0 0 1 1 0-1 0 0 1 1 0 1 0 0-0 1 1 1 1 1 0 0 0 0- 0 0 0 0 0 1
	1 1 0 0 0 0-0 1 1 0 1 0 1-1 1 1 0 1 0-0 0 0 0 1 0
	1 0 0 0 0 1 0-0 0 0 1 1 1 0-1 1 1 0 1 0-1 0 0 0 0 0 1-1 1 0 0 1 0 0 0 0-1 1 0 0 1 1 0 0 1- -0 1 0 1 1 0 0 0 1 0-1 1 0 1 0 1 1 1 1-0 0 1 0 0 0
	1 1 1 1 1 1 1 0 1-1 0 0 0 1 0 1-0 1 0 0 1 0 0 1 1-1 1 1 0 0 1 1 1 1 1-0 0 1 0 0 0- 1 1 1 0 1 0- 0 1 0 1 0 0 0 0 0-0 1 0 0 1 1 1-1 1 0 1 0 1 1 1 1- 0 0 0 0 0 1
	0 1 1 0 0 0 1 0 0-1 1 1 0 0 1-0 1 0 0 1 1 1-0 0 0 0 0 1-1 1 1 1 1 0 1 1 1 0-0 0 1 0 1 0 0
	0 0 0 1 1 1 0-1 1 1 0 1 0-0 0 1 0 1 1 1-1 1 0 0 1 1 1 0 0-0 0 0 0 1 0
	1 0 1 0 0 1 1-0 0 1 0 0 0-1 0 1 1 0 1 1-1 0 1 0 1 0 0-1 0 0 1 1 0 0 0 1-0 1 1 1 1 0 1 0 0 0- 0 0 0 0 1 0

Краткие теоретические сведения.

Каждое слово сообщения A при равномерном кодировании допускает разложение вида A =A_i1,A_i2 ,A_i3,…A_in, и имеет единственное такое разложение. Если ограничиться бинарным кодированием, то A_i = a₁ a₂ a₃…..a_m номера слов в словаре, записанные в двоичной системе (a_i принимает значения 0 или1). Необходимо отметить, что каждый двоичный номер слова может быть однозначно записан и десятеричным числом.

Пусть S”( I) – подмножество всех слов, допускающих разложение указанного вида. Рассмотрим следующую схему кодирования:

A₁® B₁

A₂® B₂

A₃® B₃ (2.1)

….

A_s® B_s ,

где B_i = b₁ b₂ b₃ …b_l – элементарные двоичные коды, имеющие одинаковую длину l = m + k , при этом такие, чтобы по коду, полученному на выходе канала связи (помеха может изменить 0 на 1 или наоборот, но не может добавить или убрать элементb_i) однозначно восстановить код на входе канала и из него получить исходное сообщение.

 

Построение самокорректирующихся кодов было осуществлено Хеммингом. Рассмотрим случай, когда источник помех может внести не более одного инвертирования в элементарный код B_i (р =1 ). Вариантов получения элементарного кода B_i будет l +1 (правильный и l штук с инвертированием b_i на каждой позиции). Для того, чтобы дополнительных разрядов в коде B_i хватило для кодирования l +1 случаев, необходимо выполнение следующего условия:

2^m ≤ 2^l / (l + 1) (2.2)

Из этих соображений выбираем l как наименьшее целое число, удовлетворяющее неравенству (2).

Дальнейшее построение будет состоять из трех этапов:

1. Построение кодов Хемминга (описание алгоритма кодирования).

2. Обнаружение ошибок в кодах Хемминга.

3. Декодирование.

 

Построение кодов Хемминга (описание алгоритма кодирования)

В множестве натуральных чисел {1,2,3,…, l }выделим следующие подмножества:

1, 3, 5, 7, 9 ….(содержатся все числа, у которых при переводе в двоичную запись в последнем разряде 1);

2, 3, 6, 7, 10 ….(содержатся все числа, у которых при переводе в двоичную запись в предпоследнем разряде 1);

. . . . . . . . . .

2^k–1, 2^k–1 +1, ….(содержатся все числа, у которых при переводе в двоичную запись в k–ом, считая справа, разряде 1).

Наименьшие члены этих подмножеств являются степенями 2: 1 = 2⁰ ; 2 = 2¹;

4 = 2²;…., причем 2^k–1 ≤ l , а 2^k+1 ³ l+1.

Члены b_i набора b₁ b₂ b₃ …b_l , у которых индекс i принадлежит множеству {1, 2, 4,… 2^k–1}, называются контрольными членами, остальные – информационными. Таким образом, контрольных членов будет k, а информационных l – k = m. Сформулируем правило построения набора …b_l по набору a₁ a₂ a₃…..a_m.

Сначала определяются информационные члены:

b₃ = a₁

b₅ = a₂

b₆ = a₃

. . . . .

Таким образом, набор информационных членов, расположенных в естественном порядке, совпадает с набором a₁ a₂ a₃…..a_m . Затем определяются контрольные члены,

b₁ = b₃+ b₅ + b₇ + …(mod 2),

b₂ = b₃+ b₆ + b₇ + …(mod 2), (2.3)

b₄= b₃+ b₆ + b₇ + …(mod 2),

. . . . . . . . . . . . .

 

значения которых 0 или 1 и помещаются на соответствующих местах в элементарных кодах B_i . По сути, создается кодовый словарь для схемы кодирования (1), в котором для каждого элементарного кода выполняются следующие условия (суммирование по mod 2):

b₁ + b₃+ b₅ + b₇ +…= 0,

b₂ + b₃+ b₆ + b₇ + …= 0, (2.4)

b₄ + b₃+ b₆ + b₇ + …= 0,

. . . . . . . . . . . . .

(количество единиц в позициях элементарного кода, определяемых индексами, четно).

 

Обнаружение ошибок в кодах Хемминга

Ошибка на выходе из канала связи может быть обнаружена и исправлена так (для построенного кода – не больше одной в каждом элементарном коде). Номер позиции S (записанный в двоичной системе), в которой произошла ошибка, определяется так:

S = S_k… S₂ S₁ ,

где S_i определяется по формулам (4) для элементарного кода, полученного на выходе канала связи. Если ошибки нет, то S_i = 0 и общий результат S = 0.

 

Пример 1: Пусть на вход канала связи поступил элементарный код 0110011 (т.е закодировано **1*011 (поз. 3,5,6,7– информационные, а контрольные члены заменены * )). На выходе получено 0110001 (искажен 6–й член элементарного кода). Вычислим S.

S₁ = b₁ + b₃+ b₅ + b₇ = 0 + 1 + 0 + 1 = 0 (mod 2),

S₂= b₂ + b₃+ b₆ + b₇ = 1 + 1 + 0 + 1 = 1 (mod 2),

S₃= b₄ + b₅ + b₆ + b₇ = 0 + 0 + 0 + 1 = 1 (mod 2).

S= 1 1 0 = 6 (в десятичной системе).

Пример 2:Пусть на выходе получено 0111011 (искажен 4–й (контрольный) член элементарного кода).

S₁ = b₁ + b₃+ b₅ + b₇ = 0 + 1 + 0 + 1 = 0 (mod 2),

S₂= b₂ + b₃+ b₆ + b₇ = 1 + 1 + 1 + 1 = 0 (mod 2),

S₃= b₄+ b₅ + b₆ + b₇ = 1 + 0 + 1 + 1 = 1 (mod 2).

S= S₃ S₂ S₁=1 0 0 = 4 (в десятичной системе).

Тогда восстановленное сообщение имеет вид: 0110011, а исходное сообщение – 1011(удалены контрольные члены, выделенные цветом)

Декодирование

После получения закодированного сообщения происходит его разбивка на элементарные коды, вычисление для каждого кода Sи в случае его неравенства 0 – корректировка соответствующего информационного члена (если S указывает на контрольный член, то корректировка не нужна). После удаления всех контрольных членов получаем исходное сообщение.

 

Примечание: Рассмотрено построение кодов Хемминга для бинарного кодирования и допустимом числе ошибок в элементарных кодах не более одной. Существует теория для построения таких кодов для равномерного кодирования любой арности и числе ошибок не более 2, 3,… и. д.

Лабораторная работа №3

Формальные грамматики и языки|речь|.

(Цепочки. Классификация грамматик по Хомскому).

 

Цель работы: закрепить понятия «алфавит», «цепочка», «формальная грамматика» и «формальный язык», «выводимость цепочек», «эквивалентная грамматика»;сформировать умения и навыки распознавания типов формальных языков и грамматик по классификации Хомского, построения эквивалентных грамматик.

 

Задание.

1.Определить к какому типу по Хомскому относится данная грамматика, какой язык она порождает, каков тип языка.

2.Указать максимально возможный номер типа грамматики и языка.

 

Вариант	Задание