
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автоматизация процедуры считывания и минимизации логических функций с помощью метода карт КарноСодержание книги
Поиск на нашем сайте
Как мы уже видели в предыдущем разделе, грамотно проведенные эквивалентные преобразования позволяют упростить логические функции и, следовательно, удешевить и сделать более надежной аппаратную реализацию соответствующих устройств. Для минимизации логических функций разработаны четкие алгоритмы, позволяющие автоматизировать этот процесс. Одним из наиболее распространенных алгоритмов минимизации является метод карт Карно. Карты Карно представляют собой специальным образом организованные таблицы соответствия. Столбцы и строки таблицы соответствуют всевозможным наборам значений не более двух переменных. Таким образом карты Карно не позволяют работать с функцией более, чем четырех аргументов. При этом наборы расположены в таком порядке, что каждый последующий элемент отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством. На рис.9.1 показаны карты Карно для двух, трех и четырех переменных.
Рис. 9.1
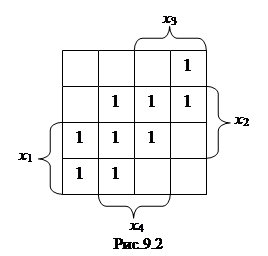
Клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписывают, и им соответствуют пустые клетки). Для упрощения, строки и столбцы, соответствующие значениям 1 для некоторой переменной, выделяют скобкой. На рис.9.2 показана карта Карно для функции Рассмотрим на примере считывание минитермов из таблицы соответствия, представленной на рис.9.2. Выделим в таблице прямоугольные области (содержащие 1, 2, 4 или 8 клеток), соответствующие значениям функции, равным 1 (рис.9.3). Выделенная область называется областью минимального покрытия.
Рассмотрим первую слева область. Она характеризуется значением х 1, равным единице, и х 3, равным нулю. Следовательно в минитерме будет присутствовать х 1 непосредственно и х 3 в виде отрицания. Переменные х 2 и х 4 не остаются постоянными внутри данной области и в соответствующем минитерме не учитываются. Таким образом, данная область описывается минитермом
Правильно проведенное считывание на основе карт Карно сразу дает тупиковую форму. Остается только выбрать из всех тупиковых форм минимальную, т.е. содержащую в своем описании наименьшее количество букв.
Пример Пусть функция трех переменных y (x 1, x 2, x 3) задана следующей таблицей:
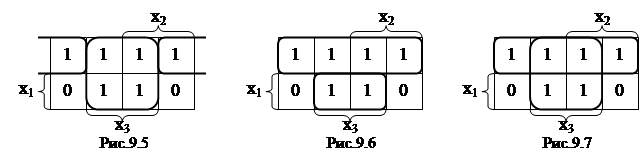
Преобразуем исходную таблицу соответствия в карту Карно (рис.9.4). Выделим в полученной таблице область минимального покрытия. Очевидно, что способов разбиения этой области может существовать несколько. Каждому способу будет соответствовать свое аналитическое описание функции. Рассмотрим для примера три различных способа разбиения (рис.9.5, 9.6, 9.7).
На каждом из рисунков получилось по две области. На рис.9.5 одна из областей объединяет элементы левого и правого крайнего столбцов таблицы. Вспомним, что эти столбцы карты Карно рассматриваются как соседние (аналогично – первая и последняя строки), поскольку отличаются значением только одной переменной (в данном случае х 2). На рис.9.7 области пересекаются между собой, что также допустимо. Выпишем соответствующие всем этим областям минитермы (рис.9.8, 9.9, 9.10).
Теперь можно построить аналитическое описание заданной таблично функции. Оно будет представлять собой дизъюнкцию полученных минитермов (т.е. дизъюнктивную нормальную форму). У нас получилось три варианта такой записи (для рис.9.8, 9.9 и 9.10, соответственно):
Очевидно, что минимальной формой является третье из полученных выражений. Оно содержит всего две переменных. Два первых выражения могут быть преобразованы в третье путем следующих преобразований:
Во всех полученных аналитических выражениях отсутствует переменная x 2, т.е. в ходе формирования аналитического описания выявлено, что функция у от переменной x 2 не зависит. При технической реализации этот факт дает возможность упростить систему, так как отпадает необходимость в измерении и преобразовании показателей, на основе которых формируется значение x 2.
В принципе, независимость у от х 2 можно было установить уже на начальном этапе, проанализировав исходную таблицу соответствия. При использовании карт Карно вывод о независимости был получен автоматически, без выдвижения дополнительных гипотез и применения каких-либо дополнительных процедур.
Алгоритм получения аналитического описания функции, заданной таблично: 1. Записать таблицу соответствия в виде карты Карно. 2. Выделить область минимального покрытия, т.е. все клетки, значение функции в которых равно единице. 3. Разбить всю область минимального покрытия на прямоугольные области площадью 1, 2, 4 или 8 клеток. Желательно, чтобы количество таких областей было минимальным. Допускаются пересечения областей. 4. Выписать соответствующие всем полученным областям минитермы. 5. Образовать из полученных минитермов дизъюнктивную нормальную форму.
Вопросы и задания 9.1. При помощи карт Карно найдите минимальные формы функций трех переменных у 1(х 1, х 2, х 3), у 2(х 1, х 2, х 3), у 3(х 1, х 2, х 3), заданных таблично:
Сравните полученный результат с результатом задания 8.2.
9.2. Найдите минимальную форму функций четырех переменных у 1(х 1, х 2, х 3, х 4), у 2(х 1, х 2, х 3, х 4), у 3(х 1, х 2, х 3, х 4), заданных таблично:
Ответы 3.1. в) "ни один человек не был в космосе" 3.2. "Квадрат гипотенузы не равен сумме квадратов катетов" 3.3. "Из трех одиннадцатиметровых штрафных ударов вратарь отбивает два, три или ни одного" 3.4. "3 – простое число" и "5 – простое число"
3.7. Исходная цепь:
Простые высказывания: y – ток в новой цепи в два раза выше, чем в исходной; х 1 – новая цепь имеет вид а); х 2 – новая цепь имеет вид б); х 3 – новая цепь имеет вид в). Сложное высказывание:
3.8. Условие получения оценки 4: Условие получения оценки 1: 3.10. " Если двигатель автомобиля удалось завести, то в автомобиле есть топливо" 3.11. " Если цены на нефть растут и добыча нефти постоянна, то выручка нефтяной компании увеличивается".
3.12.
3.14. "Сумма квадратов двух сторон треугольника равна квадрату третьей стороны тогда и только тогда, когда треугольник прямоугольный" 3.15. "Предохранитель срабатывает тогда и только тогда, когда проходящий через него ток превышает допустимое значение" 3.17. а)
б)
в)
г)
Верные тождества – б), в), г).
5.1. Доказательство законов ассоциативности:
Доказательство законов поглощения:
5.2. а) б) в)
6.1. Нет, не может. Дизъюнктивной нормальной форме всегда соответствует единственная совершенная дизъюнктивная нормальная форма.
6.2. Да, может. Совершенной дизъюнктивной нормальной форме может соответствовать множество различных дизъюнктивных нормальных форм.
6.3.
6.4. Макситерму соответствует параллельное соединение нескольких ключей. Схема, соответствующая конъюнктивной нормальной форме, представляет собой последовательно соединенные элементы, каждый из которых соответствует макситерму.
7.1. Состояние лампочки (y) должно меняться при изменении состояния любого из переключателей (x 1 и x 2). Таблицу соответствия удобнее будет составлять так, чтобы каждая следующая строчка отличалась значением только одной из переменных (x 1, x 2). Один из возможных вариантов таблицы соответствия, ее аналитического описания и соответствующей переключательной схемы:
8.1. Совершенные дизъюнктивные нормальные формы:
Совершенные конъюнктивные нормальные формы:
8.2.Минимальные формы:
9.1.
Минимальные формы для функций у 1, у 2 и у 3:
9.2.Карты Карно для функций у 1, у 2 и у 3:
Минимальные формы для функций у 1, у 2 и у 3:
Библиографический список 1. Самарин Ю.П., Сахабиева Г.А. Математика для студентов вузов. Элементы теории множеств. Элементы математической логики: Учеб. пособ. Самара: СамГТУ, 2000. 26с. 2. Сигорский В.П. Математический аппарат инженера. Киев: Технiка, 1975. 768с. 3. Овчинникова Е.В., Судоплатов С.В. Математическая логика и теория алгоритмов: Учеб. пособ. М.: Инфра-М, 2004. 112с. 4. Успенский В.А., Верещагин Н.К., Плиско В.Е. Вводный курс математической логики: Учеб. пособ. М.: ФИЗМАТЛИТ, 2004. 84с. 5. Фрейденталь Х. Язык логики. М.: Наука, 1969. 136с.
Евдокимов Михаил Александрович Саркисов Виген Геннадьевич Саркисов Геннадий Арсенович
Элементы математической логики
Редактор Н. В. В е р ш и н и н а Технический редактор В. Ф. Е л и с е е в а
Подписано в печать 17.12.04 Формат 60х84 1/16. Бумага офсетная. Печать офсетная. Усл. п. л. 1,86. Усл. кр-отт. 1,86. Уч.-изд. л. 1,79. Тираж 200 экз. С.-378
Государственное образовательное учреждение высшего профессионального образования "Самарский государственный технический университет" 443100. г.Самара, Молодогвардейская, 244. Главный корпус
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.190.212 (0.008 с.) |

 .
.

 .
.

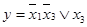


 ;
; .
. 3.5. х 1 – "ответ на 1ый вопрос – правильный", х 2 – "ответ на 2ый вопрос –правильный", и т.д. Условие получения оценки пять: х 1 х 2 х 3 х 4 х 5.
3.5. х 1 – "ответ на 1ый вопрос – правильный", х 2 – "ответ на 2ый вопрос –правильный", и т.д. Условие получения оценки пять: х 1 х 2 х 3 х 4 х 5. Примеры цепей, в которых проходящий через источник ток в два раза больше, чем в исходной цепи:
Примеры цепей, в которых проходящий через источник ток в два раза больше, чем в исходной цепи:











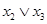









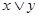



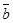
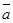


 4.1.
4.1.



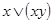

 – не является тождеством
– не является тождеством – верное тождество
– верное тождество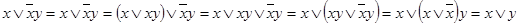 – верное тождество
– верное тождество ;
;
 ;
;
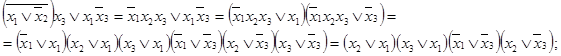

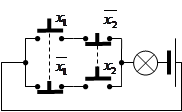

 7.2. При составлении таблицы соответствия будем действовать аналогично предыдущему заданию:
7.2. При составлении таблицы соответствия будем действовать аналогично предыдущему заданию:
 ;
; ;
;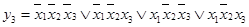 .
. ;
; ;
; .
. ;
;
 .
.

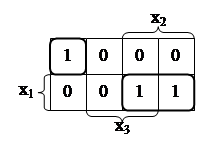 Карты Карно для функций у 1, у 2 и у 3:
Карты Карно для функций у 1, у 2 и у 3: ;
; 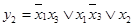 ;
;  ;
;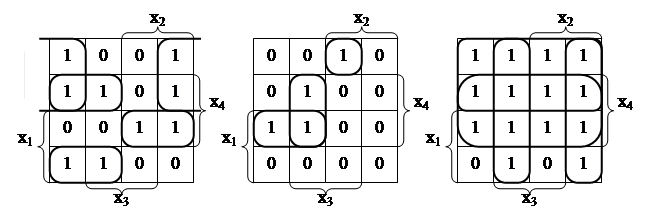
 ;
;  ;
;  .
.


