
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эквиваленция (двойная импликация)Содержание книги Поиск на нашем сайте Операция эквиваленции соответствует построению "тогда и только тогда" и обозначается символом "ó" или "≡". Эквиваленция определяется как сложное высказывание вида
Исходя из таблицы соответствия, эквиваленцию (х 1ó x 2) можно также определить как высказывание, которое истинно тогда и только тогда, когда высказывания x 1 и х 2 либо оба истинны, либо оба ложны. Так же как и импликация, операция эквиваленции очень часто применяется при формулировке различных теорем. В отличие от импликации, эквиваленция определяет необходимые и достаточные условия. Вопросы и задания 3.14. Составьте сложное высказывание с использованием операции эквиваленции из следующих простых высказываний: "Сумма квадратов двух сторон треугольника равна квадрату третьей стороны", "Треугольник прямоугольный". Проверьте результат по таблице соответствия. 3.15. С использованием операции эквиваленции сформулируйте сложное высказывание, описывающее срабатывание предохранителя в электрической цепи. 3.16. Приведите пример теоремы, при формулировке которой используется операция эквиваленции.
Принципы доказательства тождеств. Таблица операций с двумя логическими переменными Возникает вопрос: как доказать, что выражение действительно является тождеством? Есть два пути: 1. Доказательство на основе таблицы соответствия. Для обеих частей предполагаемого тождество строятся таблицы соответствия. Если эти таблицы получаются одинаковыми (т.е. для каждого набора значений аргументов значения левой и правой части выражения совпадают), то тождество верно. 2. Доказательство путем последовательных тождественных преобразований. Последовательно преобразуя левую и правую части, необходимо привести их к одинаковому виду. Правила, по которым производятся тождественные преобразования будут рассмотрены в гл.5.
Всего существует 16 операций с двумя логическими (булевыми) переменными (табл.3.6). Очевидно, что одни операции могут быть выражены через другие. Например, дизъюнкция может быть выражена через конъюнкцию и отрицание:
Существуют две операции (стрелка Пирса и штрих Шеффера), через любую из которых может быть выражена любая другая операция. Например:
Множество всех булевых функций вместе с операциями отрицания, конъюнкции и дизъюнкции образуют булеву алгебру.
Вопросы и задания 3.17. При помощи таблиц соответствия проверьте, какие из следующих выражений являются верными тождествами: а) б) в) г)
Примеры практического приложения булевой алгебры. Переключательные схемы Математический аппарат булевой алгебры нашел широкое применение при проектировании технических устройств различной природы – электрических, механических, пневматических, электромагнитных, электронных, гидравлических и многих других. В качестве примера рассмотрим электрическую схему, состоящую из источника напряжения (батареи), лампочки и одного или двух ключей (х 1 и х 2). Ключи управляются кнопками с двумя состояниями: 1 (кнопка нажата) и 0 (кнопка отпущена). Если в исходном состоянии ключ разомкнут, то при нажатии кнопки он замыкается (такой ключ – нормально разомкнутый). Ключ может быть сконструирован и так, что в исходном состоянии он замкнут (нормально замкнутый ключ), тогда нажатие кнопки означает его размыкание, т.е. приводит к противоположному результату. Поэтому нормально замкнутые ключи обозначим через При соответствующих состояниях кнопок лампочка принимает одно из двух состояний: горит (1) и не горит (0). Состояния кнопок отождествляются со значениями булевых переменных х 1 и х 2, а состояние лампочки – со значениями функции f (x 1, х 2) этих переменных.
Операции отрицания соответствует переключательная схема с одним нормально замкнутым ключом (рис.4.1). Если кнопка нажата (х =1), ключ размокнут и лампочка не горит, т.е. f (x)=0; при отпущенной кнопке (х =0) ключ замкнут и лампочка горит, т.е. f (x)=1. Операциям дизъюнкции и конъюнкции соответствуют схемы с двумя нормально разомкнутыми ключами (рис.4.2, 4.3). Легко убедиться, что в схеме на рис.4.2 лампочка горит при нажатии хотя бы одной из кнопок, а в схеме на рис.4.3 – только при нажатии обеих кнопок одновременно. Любую булеву функцию, даже самую сложную, можно представить переключательной схемой.
На рис.4.4 показана схема, реализующая функцию Вопросы и задания 4.1. Постройте переключательные схемы, соответствующие следующим функциям: а) б)
5. Тождественные преобразования Как видно на рис.4.4 и рис.4.5, одна и та же булева функция может быть реализована различными переключательными схемами и описана разными формулами. Далее рассмотрим правила тождественного преобразования булевых функций. На основании таблиц соответствия нетрудно убедиться в справедливости следующих тождеств (свойств) булевой алгебры: 1) коммутативность:
2) ассоциативность:
3) дистрибутивность:
4) свойство констант:
5) свойство отрицания:
Рассмотрим для примера доказательство первого из законов дистрибутивности с помощью таблицы соответствия. Для этого построим таблицы соответствия для левой и правой частей предполагаемого тождества (см.табл.5.1).
Как видно из табл.5.1, значения левой и правой части (выделены жирным шрифтом) совпадают при всех значениях переменных, что и требовалось доказать. Аналогично, путем построения таблиц соответствия, могут быть доказаны и другие приведенные выше тождества. Эти свойства позволяют получить ряд других важных законов и тождеств уже без обращения к таблицам соответствия: 1) законы де Моргана:
2) законы поглощения:
3) законы идемпотентности:
Докажем справедливость первого из законов де Моргана. Для этого равенство Из равенства
т.е.
После раскрытия скобок получим следующее:
Так как
Используя свойства констант (
Таким образом, путем эквивалентных преобразований мы привели выражение первого закона де Моргана к тождеству и этим доказали справедливость данного закона.
Второй закон де Моргана может быть легко получен на основе первого путем отрицания левой и правой части и соответствующей замены переменных. Запишем первый закон де Моргана относительно переменных a и b:
Если равны сами выражения, то равны и их отрицания:
Из свойств двойного отрицания:
Произведем замену переменных:
После замены получим:
т.е. второй из законов де Моргана.
Также имеют место следующие тождества:
Вопросы и задания 5.1. Докажите с помощью таблицы соответствия справедливость законов ассоциативности и поглощения. 5.2. Путем последовательных преобразований проверьте, какие из следующих выражений являются верными тождествами: а) б) в) Сравните полученные результаты с результатами задания 3.15.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

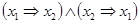 . Построим таблицу соответствия (табл.3.5) при помощи таблиц для импликаций
. Построим таблицу соответствия (табл.3.5) при помощи таблиц для импликаций  и
и 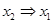 .
.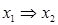

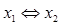
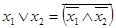

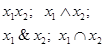


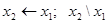










 ;
; ;
; ;
; .
.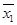 и
и  .
.

 . Та же функция представляется равносильной формулой
. Та же функция представляется равносильной формулой  , которой соответствует более простая схема (рис.4.5). Следует иметь ввиду, что ключи, обозначенные одинаковыми буквами (например, х 1 и
, которой соответствует более простая схема (рис.4.5). Следует иметь ввиду, что ключи, обозначенные одинаковыми буквами (например, х 1 и 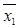 ), связаны между собой и управляются общей кнопкой, так как они описываются одной и той же переменной.
), связаны между собой и управляются общей кнопкой, так как они описываются одной и той же переменной. ;
; .
. ;
; ;
; ;
; ;
; .
.

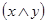


 ;
; ;
;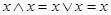 .
. путем последовательных преобразований сведем к очевидному тождеству.
путем последовательных преобразований сведем к очевидному тождеству.
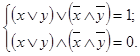

 и
и  , а
, а  и
и  , то предыдущее выражение можно представить в следующем виде:
, то предыдущее выражение можно представить в следующем виде:
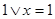 ,
,  ,
, 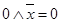 ,
,  ), получаем
), получаем – очевидное тождество.
– очевидное тождество. .
. .
. .
.
 ,
,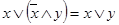 ;
;  ;
;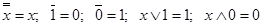 и т.д.
и т.д.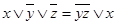 ;
;


