
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
М. А. Евдокимов, В. Г. Саркисов, Г. А. СаркисовСодержание книги Поиск на нашем сайте М.А.Евдокимов, В.Г.Саркисов, Г.А.Саркисов
Элементы математической логики
Учебно-методическое пособие
Самара 2004
УДК 51 Элементы математической логики: Учеб.-метод.пособ. / М.А.Евдокимов, В.Г.Саркисов, Г.А.Саркисов; Самар. гос. техн. ун-т. Самара 2004, с.33.
Рассмотрены основные логические операции, принципы доказательства логических тождеств. Описаны примеры практического применения алгебры логики, алгоритмы получения аналитического описания и минимизации логических функций. Особое внимание уделено объяснениям основных понятий и примерам. Предназначено для самостоятельного изучения основ математической логики и приобретения базовых навыков решения прикладных задач студентами инженерных, экономических и других нематематических вузовских специальностей.
ISBN 5-7964-0625-6.
Ил. 27. Табл. 23. Библиогр.: 5 назв.
Печатается по решению редакционно-издательского совета Самарского государственного технического университета
Рецензент: д-р. техн. наук Н. Н. С т о л я р о в
Оглавление
1. Введение. 4 2. Понятие высказывания. Понятие операции. 4 3. Основные логические операции. 6 3.1. Инверсия (отрицание) 6 3.2. Конъюнкция (логическое умножение) 7 3.3. Дизъюнкция (логическое сложение) 7 3.4. Импликация (логическое следование) 8 3.5. Эквиваленция (двойная импликация) 10 3.6. Принципы доказательства тождеств. Таблица операций с двумя логическими 4. Примеры практического приложения булевой алгебры. Переключательные схемы.. 13 5. Тождественные преобразования. 14 6. Дизъюнктивная и конъюнктивная нормальные формы булевой функции (дизъюнкция 7. Построение аналитического выражения булевой функции по таблице ее значений. 18 8. Минимизация логических функций, оптимизация технической реализации функций 9. Автоматизация процедуры считывания и минимизации логических функций с Ответы.. 27 Библиографический список. 32
Логика как искусство рассуждений зародилась в глубокой древности. Начало науки о законах и формах рассуждений связывают с именем Аристотеля. Прошло два тысячелетия, прежде чем Лейбниц предложил ввести в логику математическую символику и использовать ее для общих логических построений. Эту идею последовательно реализовал в позапрошлом столетии Джордж Буль и тем самым заложил основы математической (символической) логики. Главная цель применения в логике математической символики заключалась в том, чтобы свести операции с логическими заключениями к формальным действиям над символами. При этом исходные положения записываются формулами, которые преобразуются по определенным законам, а полученные результаты истолковываются в соответствующих понятиях. Бурное развитие математической логики связано, прежде всего, с задачами обоснования математики, где она используется для доказательства непротиворечивости исходных понятий и правильности рассуждений и выводов математических теорий. Во второй половине ХХ века логика получила широкое применение в технике при исследовании и разработке релейно-контактных схем, вычислительных машин, дискретных автоматов. Ее методы используются в теории преобразования и передачи информации, теории вероятностей и комбинаторном анализе. Математическая логика внедряется в такие области как экономика, биология, медицина, психология, языкознание, право. Столь интенсивный выход математической логики за пределы математики объясняется тем, что ее аппарат легко распространяется на объекты самой общей природы, лишь бы они только характеризовались конечным числом состояний. С расширением областей применения и дальнейшим развитием математической логики изменяется и взгляд на нее. Объектами математической логики являются любые конечные дискретные системы, а ее главная задача – структурное моделирование таких систем.
Понятие высказывания. Понятие операции Основным объектом, изучаемым математической логикой является высказывание. Высказывание – любое предложение, относительно которого известно, является оно истинным (И) или ложным (Л).
Примеры 1. "Наталья – мужское имя" – ложное высказывание. 2. "Сопротивление и ёмкость – параметры электрических цепей" – истинное высказывание. 3. "Среднее расстояние от Земли до Солнца составляет 150 000 000 км." – можно рассматривать как истинное или ложное высказывание в зависимости от величины допустимых погрешностей. 4. "Соблюдайте технику безопасности" – не является высказыванием.
Математическая логика не изучает содержание высказываний. Для нее существенна лишь их истинность или ложность. В данном курсе рассматривается двузначная логика, которая имеет дело с объектами, принимающими одно из двух возможных состояний – истина или ложь, высокое или низкое напряжение, наличие или отсутствие некоторого признака у объекта и т.д. Объекты, которые могут принимать значения из конечного множества, содержащего более двух элементов, называются многозначными. Такие объекты либо сводятся некоторым образом к двузначным, либо обслуживаются аппаратом многозначной логики. В данном курсе рассматривается двузначная логика, которая широко применяется при разработке компьютеров, контроллеров и других технических устройств. Объекты с двумя возможными состояниями (в том числе и высказывания) характеризуются булевыми переменными, которые способны принимать лишь два различных значения. Для обозначения этих значений используют цифры 0 и 1 или буквы Л (ложь) и И (истина). Отношения между булевыми переменными представляются булевыми функциями, которые (подобно числовым функциям) могут зависеть от одного, двух и более аргументов. Далее будем обозначать аргументы буквами xi (i =1,2,…), а булевы функции буквами yj (j =1,2,…). Булевы функции можно рассматривать как логические операции. Исходные, первоначальные высказывания, относительно которых заранее известна их истинность или ложность, называются простыми высказываниями. Выполняя над простыми высказываниями те или иные действия (в терминах математической логики – операции), можно образовывать сложные высказывания. Их истинность или ложность можно установить, опираясь на сведения о простых высказываниях. В разговорном языке операциям над высказываниями соответствуют логические связки "если …, то …", "… и …", "… или …", "не …" и др.
Примеры 1. " a < b ", " b < c ", " a < c " – простые высказывания; " Если a < b и b < c, то a < c " – сложное высказывание (подчеркнуты логические связки). 2. "Напряжение в сети 220 В", "частота 50 Гц" – простые высказывания; "напряжение в сети 220 В и частота 50 Гц" – сложное высказывание. 3. " Если начальная скорость равна нулю и ускорение а – постоянная величина, то пройденный за время t путь S вычисляется по формуле S = at 2/2" – сложное высказывание. Выделим простые высказывания, составляющие данное сложное высказывание: "начальная скорость равна нулю", "ускорение а – постоянная величина", "пройденный за время t путь S вычисляется по формуле S = at 2/2".
Вопросы и задания 2.1. Как определить, является ли предложение высказыванием? 2.2. Сформулируйте самостоятельно примеры истинных и ложных высказываний, а также предложений, не являющихся высказываниями. 2.3. Приведите примеры сложных высказываний. Выделите в каждом из них простые высказывания. Основные логические операции Инверсия (отрицание) Простейшей логической операцией является инверсия. Операция инверсии соответствует частице "не", обозначается символами "¯" или "". Отрицанием истинного высказывания является ложное высказывание, а отрицанием ложного – истинное. Отрицание определяется таблицей соответствия (табл.3.1).
Пример Высказывание х: "Все насекомые имеют крылья". Инверсией высказывания х является следующее высказывание
Очевидное свойство отрицания:
Вопросы и задания 3.1. Какое из следующих высказываний является отрицанием для высказывания "Некоторые люди были в космосе": а) "Некоторые люди не были в космосе"; б) "Все люди были в космосе"; в) "Ни один человек не был в космосе". Проверьте правильность ответа по таблице соответствия, принимая исходное высказывание: 1) за истинное 2) за ложное. 3.2. Сформулируйте отрицание для высказывания "Квадрат гипотенузы равен сумме квадратов катетов". 3.3. Сформулируйте отрицание для высказывания "Вратарь отбивает один из трех одиннадцатиметровых штрафных ударов".
Пример Высказывание х 1 – "В течение 10 минут на остановку подъедет автобус 1-го маршрута". Высказывание х 2 – "В течение 10 минут на остановку подъедет автобус 2-го маршрута". Для того, чтобы сложное высказывание х 1 х 2 было истинным, должно быть истинным каждое из простых высказываний х 1 и х 2. Таким образом, конъюнкция двух исходных высказываний Вопросы и задания 3.4. Представьте высказывание "3 и 5 – простые числа" в виде конъюнкции двух высказываний. 3.5. В экзаменационном билете пять вопросов. Правильный ответ на каждый вопрос дает один балл. Сформулируйте простые высказывания, описывающие правильность ответа на вопрос. Составьте из них сложное высказывание, описывающее условие получения оценки пять. 3.6. Приведите пример теоремы, в условии которой содержится конъюнкция. Пример Высказывание х 1: "В течение 10 минут на остановку подъедет автобус 1-го маршрута". Высказывание х 2: "В течение 10 минут на остановку подъедет автобус 2-го маршрута". Дизъюнкция этих двух высказываний
Вопросы и задания 3.7. Составьте схему электрической цепи, состоящей из идеального источника напряжения Е и сопротивления R. Сформулируйте несколько способов образования новой электрической цепи (путем добавления сопротивлений R и/или источников напряжения E), в которой проходящий через источник ток в два раза больше, чем в исходной. Сформулируйте сложное высказывание, описывающее все предложенные способы. 3.8. По условиям задачи 3.5 составьте сложные высказывания, описывающие условия получения оценок 4 и 1. 3.9. Приведите пример теоремы, в условии которой содержится дизъюнкция.
Пример 1. "5=2·2 и 5·2=8" – ложное высказывание х1. Подставим во вторую часть этого ложного высказывания "5·2=8" значение "5" из первой части "(5=2·2)·2=8" и получим вывод х2: "(2·2)·2=8", который является истинным высказыванием. 2. "На Луне есть атмосфера" – ложное высказывание х1. Если речь идет о присутствии (или отсутствии) на Луне атмосферы, то вполне логично предположить, что речь идет о планете. Отсюда можно сделать вывод, что Луна является планетой. "Луна является планетой" – истинный вывод х2, полученный из ложной предпосылки х1.
Третья строка: "Из истинного х 1 следует ложное х 2 – это ложь". Из истинных предпосылок корректными методами нельзя получить ложное заключение. Четвертая строка: "Из истинного х 1 следует истинное х 2 – это истина". Смысл этой строки очевиден. Операция импликации описывает достаточные, но не необходимые условия теоремы. Вспомним, что математическая логика не занимается исследованием содержания высказываний, а рассматривает их только с точки зрения истинности и ложности. Поэтому с формальной точки зрения одно истинное высказывание может быть заменено другим истинным независимо от их содержания. При этом могут образовываться совершенно не связанные между собой высказывания с точки зрения смыслового содержания.
Пример Высказывание х1: "Сила тока обратно пропорциональна сопротивлению" – истинное. Высказывание х2: "На экзамене есть четыре варианта отметок – отлично, хорошо, удовлетворительно и неудовлетворительно" – также истинное. Эти высказывания не связаны между собой по содержанию причинно-следственной связью. Однако, с точки зрения математической логики импликация
При аппаратной реализации логических схем замена одного истинного высказывания другим истинным (или ложного другим ложным) уже не выглядит чем-то необычным. Вспомним, что при аппаратной реализации истинность и ложность характеризуются какой-либо физической величиной, имеющей два возможных состояния (высокое и низкое напряжения в электрических схемах, высокое и низкое давления в пневматических и гидравлических устройствах). Очевидно, что высокое напряжение, соответствующее одному истинному высказыванию, ничем не отличается от высокого напряжения, соответствующего другому истинному высказыванию. Следовательно, такая замена вполне допустима. Вопросы и задания 3.10. Из простых высказываний "В автомобиле есть топливо" и "Двигатель автомобиля удалось завести" составьте сложное высказывание с использованием операции импликации. Проверьте результат по таблице соответствия. 3.11. Составьте сложное высказывание с использованием операций импликации и конъюнкции из следующих простых высказываний: "Цены на нефть растут", "Добыча нефти постоянна", "Выручка нефтяной компании увеличивается". Проверьте полученный ответ при помощи таблиц соответствия. 3.12. Импликация описывает достаточные, но не необходимые условия теоремы. Запишите таблицу соответствия для операции, описывающей необходимые, но не достаточные условия. 3.13. Приведите пример теоремы, при формулировке которой используется операция импликации.
Принципы доказательства тождеств. Таблица операций с двумя логическими переменными Возникает вопрос: как доказать, что выражение действительно является тождеством? Есть два пути: 1. Доказательство на основе таблицы соответствия. Для обеих частей предполагаемого тождество строятся таблицы соответствия. Если эти таблицы получаются одинаковыми (т.е. для каждого набора значений аргументов значения левой и правой части выражения совпадают), то тождество верно. 2. Доказательство путем последовательных тождественных преобразований. Последовательно преобразуя левую и правую части, необходимо привести их к одинаковому виду. Правила, по которым производятся тождественные преобразования будут рассмотрены в гл.5.
Всего существует 16 операций с двумя логическими (булевыми) переменными (табл.3.6). Очевидно, что одни операции могут быть выражены через другие. Например, дизъюнкция может быть выражена через конъюнкцию и отрицание:
Существуют две операции (стрелка Пирса и штрих Шеффера), через любую из которых может быть выражена любая другая операция. Например:
Множество всех булевых функций вместе с операциями отрицания, конъюнкции и дизъюнкции образуют булеву алгебру.
Вопросы и задания 3.17. При помощи таблиц соответствия проверьте, какие из следующих выражений являются верными тождествами: а) б) в) г)
Примеры практического приложения булевой алгебры. Переключательные схемы Математический аппарат булевой алгебры нашел широкое применение при проектировании технических устройств различной природы – электрических, механических, пневматических, электромагнитных, электронных, гидравлических и многих других. В качестве примера рассмотрим электрическую схему, состоящую из источника напряжения (батареи), лампочки и одного или двух ключей (х 1 и х 2). Ключи управляются кнопками с двумя состояниями: 1 (кнопка нажата) и 0 (кнопка отпущена). Если в исходном состоянии ключ разомкнут, то при нажатии кнопки он замыкается (такой ключ – нормально разомкнутый). Ключ может быть сконструирован и так, что в исходном состоянии он замкнут (нормально замкнутый ключ), тогда нажатие кнопки означает его размыкание, т.е. приводит к противоположному результату. Поэтому нормально замкнутые ключи обозначим через При соответствующих состояниях кнопок лампочка принимает одно из двух состояний: горит (1) и не горит (0). Состояния кнопок отождествляются со значениями булевых переменных х 1 и х 2, а состояние лампочки – со значениями функции f (x 1, х 2) этих переменных.
Операции отрицания соответствует переключательная схема с одним нормально замкнутым ключом (рис.4.1). Если кнопка нажата (х =1), ключ размокнут и лампочка не горит, т.е. f (x)=0; при отпущенной кнопке (х =0) ключ замкнут и лампочка горит, т.е. f (x)=1. Операциям дизъюнкции и конъюнкции соответствуют схемы с двумя нормально разомкнутыми ключами (рис.4.2, 4.3). Легко убедиться, что в схеме на рис.4.2 лампочка горит при нажатии хотя бы одной из кнопок, а в схеме на рис.4.3 – только при нажатии обеих кнопок одновременно. Любую булеву функцию, даже самую сложную, можно представить переключательной схемой.
На рис.4.4 показана схема, реализующая функцию Вопросы и задания 4.1. Постройте переключательные схемы, соответствующие следующим функциям: а) б)
5. Тождественные преобразования Как видно на рис.4.4 и рис.4.5, одна и та же булева функция может быть реализована различными переключательными схемами и описана разными формулами. Далее рассмотрим правила тождественного преобразования булевых функций. На основании таблиц соответствия нетрудно убедиться в справедливости следующих тождеств (свойств) булевой алгебры: 1) коммутативность:
2) ассоциативность:
3) дистрибутивность:
4) свойство констант:
5) свойство отрицания:
Рассмотрим для примера доказательство первого из законов дистрибутивности с помощью таблицы соответствия. Для этого построим таблицы соответствия для левой и правой частей предполагаемого тождества (см.табл.5.1).
Как видно из табл.5.1, значения левой и правой части (выделены жирным шрифтом) совпадают при всех значениях переменных, что и требовалось доказать. Аналогично, путем построения таблиц соответствия, могут быть доказаны и другие приведенные выше тождества. Эти свойства позволяют получить ряд других важных законов и тождеств уже без обращения к таблицам соответствия: 1) законы де Моргана:
2) законы поглощения:
3) законы идемпотентности:
Докажем справедливость первого из законов де Моргана. Для этого равенство Из равенства
т.е.
После раскрытия скобок получим следующее:
Так как
Используя свойства констант (
Таким образом, путем эквивалентных преобразований мы привели выражение первого закона де Моргана к тождеству и этим доказали справедливость данного закона.
Второй закон де Моргана может быть легко получен на основе первого путем отрицания левой и правой части и соответствующей замены переменных. Запишем первый закон де Моргана относительно переменных a и b:
Если равны сами выражения, то равны и их отрицания:
Из свойств двойного отрицания:
Произведем замену переменных:
После замены получим:
т.е. второй из законов де Моргана.
Также имеют место следующие тождества:
Вопросы и задания 5.1. Докажите с помощью таблицы соответствия справедливость законов ассоциативности и поглощения. 5.2. Путем последовательных преобразований проверьте, какие из следующих выражений являются верными тождествами: а) б) в) Сравните полученные результаты с результатами задания 3.15.
Пример
Формулы приводятся к нормальной форме следующим путем: 1) с помощью законов де Моргана формула преобразуется к такому виду, чтобы знаки отрицания относились только к отдельным переменным; 2) на основе первого (второго) дистрибутивного закона формула сводится к дизъюнкции конъюнкций (конъюнкции дизъюнкций); 3) полученные выражения упрощаются в соответствии с тождествами
Пример Привести к дизъюнктивной и конъюнктивной нормальным формам функцию Решение В соответствии с законом де Моргана преобразуем
На основе законов дистрибутивности раскроем скобки:
В соответствии с законом идемпотентности
Полученное выражение является дизъюнктивной нормальной формой. Аналогичным образом представим заданную функцию в конъюнктивной нормальной форме:
Конъюнктивная нормальная форма получена.
Члены дизъюнктивной (конъюнктивной) нормальной формы, представляющие собой элементарные конъюнкции (дизъюнкции) k букв, называются минитермами (макситермами) k- го ранга. Так, например, Совершенной дизъюнктивной (конъюнктивной) нормальной формой называется дизъюнктивная (конъюнктивная) нормальная форма, каждый минитерм (макситерм) которой содержит все переменные (либо в прямом, либо в инверсном виде). Например, минитерм
Вопросы и задания 6.1. Может ли одной и той же дизъюнктивной нормальной форме соответствовать несколько различных совершенных дизъюнктивных нормальных форм? 6.2. Может ли одной и той же совершенной дизъюнктивной нормальной форме соответствовать несколько различных дизъюнктивных нормальных форм? 6.3. Представьте функцию трех переменных а) в дизъюнктивной нормальной форме; б) в совершенной дизъюнктивной нормальной форме; в) в конъюнктивной нормальной форме; г) в совершенной конъюнктивной нормальной форме. 6.4. Схема, представленная на рис.4.4 соответствует дизъюнктивной нормальной форме. Каждая ветвь цепи соответствует одному минитерму. Какая цепь соответствует макситерму? Каков общий вид схемы, соответствующей конъюнктивной нормальной форме?
Пример Пусть функция трех переменных y (x 1, x 2, x 3) задана следующей таблицей:
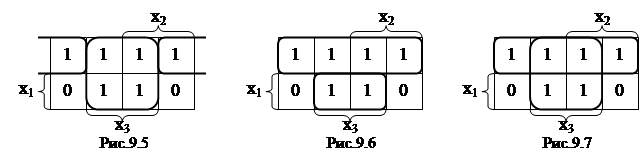
Преобразуем исходную таблицу соответствия в карту Карно (рис.9.4). Выделим в полученной таблице область минимального покрытия. Очевидно, что способов разбиения этой области может существовать несколько. Каждому способу будет соответствовать свое аналитическое описание функции. Рассмотрим для примера три различных способа разбиения (рис.9.5, 9.6, 9.7).
На каждом из рисунков получилось по две области. На рис.9.5 одна из областей объединяет элементы левого и правого крайнего столбцов таблицы. Вспомним, что эти столбцы карты Карно рассматриваются как соседние (аналогично – первая и последняя строки), поскольку отличаются значением только одной переменной (в данном случае х 2). На рис.9.7 области пересекаются между собой, что также допустимо. Выпишем соответствующие всем этим областям минитермы (рис.9.8, 9.9, 9.10).
Теперь можно построить аналитическое описание заданной таблично функции. Оно будет представлять собой дизъюнкцию полученных минитермов (т.е. дизъюнктивную нормальную форму). У нас получилось три варианта такой записи (для рис.9.8, 9.9 и 9.10, соответственно):
Очевидно, что минимальной формой является третье из полученных выражений. Оно содержит всего две переменных. Два первых выражения могут быть преобразованы в третье путем следующих преобразований:
Во всех полученных аналитических выражениях отсутствует переменная x 2, т.е. в ходе формирования аналитического описания выявлено, что функция у от переменной x 2 не зависит. При технической реализации этот факт дает возможность упростить систему, так как отпадает необходимость в измерении и преобразовании показателей, на основе которых формируется значение x 2. В принципе, независимость у от х 2 можно было установить уже на начальном этапе, проанализиро
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |



 : "В течение 10 минут на остановку подъедут автобусы и 1-го и 2-го маршрутов".
: "В течение 10 минут на остановку подъедут автобусы и 1-го и 2-го маршрутов". : "В течение 10 минут на остановку подъедет автобус 1-го или 2-го маршрута".
: "В течение 10 минут на остановку подъедет автобус 1-го или 2-го маршрута". ("Если сила тока обратно пропорциональна сопротивлению, то на экзамене есть четыре варианта отметок – отлично, хорошо, удовлетворительно и неудовлетворительно") является истинным высказыванием.
("Если сила тока обратно пропорциональна сопротивлению, то на экзамене есть четыре варианта отметок – отлично, хорошо, удовлетворительно и неудовлетворительно") является истинным высказыванием.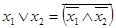

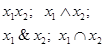


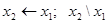










 ;
; ;
; ;
; .
.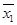 и
и  .
.

 . Та же функция представляется равносильной формулой
. Та же функция представляется равносильной формулой  , которой соответствует более простая схема (рис.4.5). Следует иметь ввиду, что ключи, обозначенные одинаковыми буквами (например, х 1 и
, которой соответствует более простая схема (рис.4.5). Следует иметь ввиду, что ключи, обозначенные одинаковыми буквами (например, х 1 и 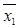 ), связаны между собой и управляются общей кнопкой, так как они описываются одной и той же переменной.
), связаны между собой и управляются общей кнопкой, так как они описываются одной и той же переменной. ;
; .
. ;
; ;
; ;
; ;
; .
.

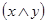


 ;
; ;
;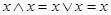 .
. путем последовательных преобразований сведем к очевидному тождеству.
путем последовательных преобразований сведем к очевидному тождеству.
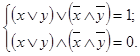

 и
и  , а
, а  и
и  , то предыдущее выражение можно представить в следующем виде:
, то предыдущее выражение можно представить в следующем виде:
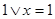 ,
,  ,
, 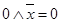 ,
,  ), получаем
), получаем – очевидное тождество.
– очевидное тождество. .
. .
. .
.
 ,
,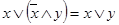 ;
;  ;
;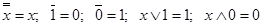 и т.д.
и т.д.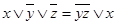 ;
; – дизъюнктивная нормальная форма
– дизъюнктивная нормальная форма – конъюнктивная нормальная форма
– конъюнктивная нормальная форма (
(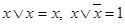 )
) .
. .
. .
. .
. . Откуда
. Откуда .
.
 .
. – минитерм третьего ранга, а
– минитерм третьего ранга, а 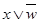 – макситерм второго ранга.
– макситерм второго ранга.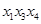 функции четырех переменных (х 1, х 2, х 3, х 4) в совершенной дизъюнктивной нормальной форме будет представлен дизъюнкцией двух минитермов:
функции четырех переменных (х 1, х 2, х 3, х 4) в совершенной дизъюнктивной нормальной форме будет представлен дизъюнкцией двух минитермов:  .
.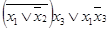


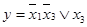


 ;
; .
.


