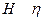Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Toward Mathematical StructureСодержание книги
Поиск на нашем сайте
Three new approaches to numbers, in 1801 and in the 1830s, were to the hint at the general concept of math structure and reveal unsuspected horizons in the whole of maths. That of 1801 was the concept of congruence, introduced by Gauss. To this and the revolutionary work (1830) of E. Galois in the theory of algebraic equations can be traced the partial execution of L. Kronecker's (1823-1891) programme in the 1880s for basing all maths on the natural numbers. The same sources are one origin of the modern abstract development of algebraic and geometric theories, in which the structure of math systems is the subject of investigation, and it is sought to obtain the interrelations of the math objectsconcerned with a minimum of calculation. "Structure" may be thought of at present in any of its intuitive meanings; it was precisely defined in 1910 by themath logicians. We shall approach math structure through the union effected In the nineteenth century between algebra and arithmetic. From the standpoint of maths as a whole, the methodology of deliberate generalization and abstraction, culminating in the twentieth century in a rapidly growing maths of structure, is doubtless the most significant contribution of all the successive attempts to extend the number concept. But at every stage of the progression from the natural numbers 1, 2, 3,... to other types of numbers, each оf several fields of maths adjacent to arithmetic was broadened and enriched. New acquisitions in other fields reacted reciprocally on arithmetic. For example, the first satisfactory theory of ordinary complex numbers to become widely known was that of Gauss (1831) devised to provide a concise solution for a special problem in Diophantine analysis. The theory of complex numbers necessitated a radical revision and generalization of the concept of arithmetical divisibility, which in turn suggested a reformulation of certain parts of algebraic geometry. The latter, in its turn, was partly responsible for further generalizations (modular systems) in the algebraic arithmetic – or arithmetical algebra – of the twentieth century. The forward movement was universal and each major advance in one department induced progress in others. The passage to final abstractness took about a quarter of a century. The turning point was Hilbert's work on the foundation of geometry in 1899. Although this did not concern algebra or arithmetic directly, it set a new and high standard of definiteness and completeness in the statement of all math definitions or, what is equivalent, in the construction of postulate systems. A general theory of structure was developed by A. N. Whitehead and B. Russell in 1910. It will suffice here to recall a cardinal definition: A relation There are six major developments in maths that greatly influenced the modern theory of numbers. They are: 1) the definition by Gauss, Kummer and Dedekind of algebraic integers; 2) the restoration of the fundamental theorem of arithmetic in algebraic number fields by Dedekind's introduction of ideals; 3) the definitive work of Galois on the solution of algebraic equations by radicals; 4) the theory of finite groups; 5) the modern theory of fields that followed; 6) the partial application of arithmetical concepts to certain linear algebras. All of these developments are closely interrelated. The last marks the farthest extension of classical arithmetic up to 1945, and it is either the climax or the beginning of a structural arithmetization of algebra, foreseen as early as 1860 by Kronecker. As if in preparation for the climax, the algebra of hypercomplex numbers rapidly outgrew its classificatory adolescence of the 1870s and became progressively more concerned with general methods reaching a certain maturity early in the twentieth century. The fifth major development, which logically would seem to be a necessary prelude to the others, strangely enough came last. Not until the closing years of the nineteenth century was anyone greatly perturbed about the natural numbers 1, 2, 3,.... All maths, from the classical arithmetic to Fermat, Euler, Lagrange, Legendre, Gauss and their numerous imitators, to geometry and analysis, had accepted these speciously simple numbers as "given". Without them, none of the major advances of modern arithmetic would ever have happened. Yet no arithmetician asked, "By whom are the natural numbers 'given'? Kronecker ascribed them to God, but this was hardly a math solution. The question arose, not in arithmetic, but in analysis. It was answered by the modern definition of cardinal and ordinal numbers. This finally united arithmetic and analysis at their common source. The sixth and last major development in the evolution of the number concept was the application of arithmetic to the differential and integral calculus. It is a point of great interest that one of the strongest initial impulses for the final application of arithmetic to analysis came from math physics. It was gradually perceived that the cardinals and ordinals 1, 2, 3,... demanded clarification. The arithmetic of 1,2,3,..., and with it math analysis, resigned its soul to the searching mercies of math logic. About twenty-five centuries of struggle to understand numbers thus ended where it had begun with Pythagoras. The modern programme is his, but with a difference. Pythagoras trusted 1,2,3,... to "explain" the Universe including maths, and the spirit animating his "explanation" was strict deductive reasoning. The natural numbers are still trusted by mathematicians and scientists in their technical maths and its applications. But math reasoning itself, vastly broadened and deepened in the twentieth century beyond the utmost ever imagined by any Greek, supplanted the natural numbers in math interest. When, if ever, math logic shall have surmounted its obscurities, the natural numbers may be clearly seen for what they "are". But there will always remain the possibility that any unsealed range may conceal a higher just beyond, and arithmeticians will come upon many things to keep them busy and incompletely satisfied for the next five thousand years. After that, perhaps, it will not matter to anyone that 1,2,3,... "are". From the great mass of work that has been done since 1900 on the arithmetization of algebra – or vice versa – one should mention the study of all possible types of fields and the relations between them. The final outcome may be roughly described as an analysis of the structure of fields with respect to their possible subfields and superfields. The next item, dating from about 1920 marks a distinct advance. It is represented by a host of mathematicians who undertook to do for an abstract ring what Dedekind has done for any ring of algebraic numbers, and to extend the Galois theory to abstract fields. Thus, the Dedekind theory of ideals was abstracted and generalized, as was also the Galois theory. The first of these may properly be assigned to arithmetic, as one of the chief objectives is the discovery, for any ring, of unique decomposition theorems analogous to the fundamental theorem of arithmetic, or to the unique representation of a Dedekind ideal as a product of prime ideals. Two basic but rather inconspicuous-looking items of the classical theory of algebraic number ideals passed unchanged into the abstract theory, "the greatest common divisor (the GCD)" and "least common multiple (LCM)". Although at the first glance these are mere details, experience has shown that they are the framework of much algebraic structure and that, when their simplest properties are restated abstractly as postulates, the resulting system unifies widely separated and apparently distinct theories of algebra and arithmetic. They lead, in fact, to what seemed the most important theory of algebraic-arithmetic structures. The rapid expansion of the theory of structures or lattices following Dedekind's introduction of dual groups is typical of much in the recent development of maths. Structures The generic concept of structure may be quite simply explained, as J. Diendonne did, namely: "If the temperature is 800 F and a 20-degree rise is predicted, we expect without counting, an eventual temperature of 1000. If we have a book open at page 80 and we are told to look 20 pages further on, we turn without hesitation to page 100 without counting the intervening pages. We are using the fact that the structure of addition applies to both cases, adding the numbers gives the correct result when interpreted either for temperatures or for pages. We do not (fortunately!) have to learn a special arithmetic for thermometers and another for books...". This is, of course, one of the simplest examples of structures, but it shows at once that the most striking feature of structures has something to do with the economy of thought and this aspect is naturally of paramount importance in maths. The structures are almost custom-made tools for mathematicians. Whenever a mathematician has been able to prove that the objects he is studying verify the axioms of a certain type of structure, he has ipso facto (by the fact itself) proved all the theorems from the theory of that type of structure for these particular objects (theorems which he would otherwise probably either miss altogether or for which he would have to devise special proofs). Simularly, whenever two given structures are proved to be isomorphic, thenumber of theorems is immediately doubled, each theorem proved for one of the structures giving at once a corresponding theorem for the other (and sometimes I it is much easier to prove one than the other). No wonder, therefore, that there existwhole theories of a highly complex and difficult nature, such as the so-called "class-field theory" in the theory of numbers, whose major aim is to prove that the two structures are isomorphic. Anyone who is familiar with the theory of groups however elementary, already knows something about the working mechanism of such structures in concrete, although he may not be explicitly aware of it. Namely, the nature of the objects or elements forming a group may vary, indeed, tremendously, but they share the same structure of group, defined by the groups themselves. If he knows, in addition, something about isomorphisms among groups, he is then even better off, since the concept of "isomorphism" is, evidently, one of those abstract notions which are closely and naturally linked to that of structure. Generally, a structure of a certain type is defined for a set Then again, there is the third type, called topological structures (or topologies). A topology is given on a set if a concept of neighbourhood or limit which satisfied certain conditions (also called axioms) is adopted for the set in a suitable manner. It yields, therefore, an abstract formulation of the more or less intuitive notion of neighbourhood (or limit of continuity) to which we were originally led by our physical sense of space. The degree of abstraction necessary for the formulation of the axioms of a topology is evidently greater than that for algebraic or order structures; but this may be considered still simple or less sophisticated in comparison with certain structures which are found strung-together, namely, mixed (or multiple) structures. For example, a structure may be both algebraic and topological, linked together by new axioms, topological algebra and algebraic topology are two specific examples of such a mixed structure (although homological algebra is still unmixed, exemplifying a pure type of structure). The mixed structure may appear also in elementary cases; for instance, the set of real numbers reveals three kinds of structures at the same time: an algebraic structure defined by computative operations (addition and multiplication), a structure of order by which inequalities between real numbers can be treated, and, finally, a topological structure where a concept of limit is explicated. These structures are obviously associated with each other so that topology may be defined by order or relations (two inequalities added term by term, etc. may exist between order and algebra). Several other structures appear strung-together, more likely at the level of advanced examples such as topological groups, differential manifolds, analytic fibre spaces, discontinuous groups of transformations, etc. These structures, pure or mixed, are now found everywhere at the concentric centre of the math universe. A considerable diversity can be observed among the greattypes of structures, some of which may be called mother structures, namely, the most general structures with the smallest number of axioms, while there are also those which are obtainable by adding more axioms such that they will yield the harvest of new consequences. Here appear, thus, a hierarchy of structures, descending from thesimple and general at the top to the complex and particular at the bottom. Farther along, at the lowest of the structural totem pole, one finally descends upon the ground of the particular and individual where certain areas have long remained or will for some time remain indeterminate, structure-wise, such that the "classical" maths begins to emerge. For example, certain fragments from the theory of numbers, of functions of a real or complex variable, of differential equations, of differential geometry, etc. Nevertheless, after the extensive reconstructions even the hard-core areas cannot but fail to retain their former autonomy; they have become crossroads, where several more general structures meet and react upon each other. For example, the redoubtable theory of primes is now a close neighbour of the theory of algebraic curves, and the most ancient Euclidean geometry borders on a brand-new theory of integral equations. One cannot hope to have a complete and final list of such types of structures on hand; several new ones have been discovered, and we have every reason to expect new discoveries of that kind. Still, there are many large chunks of classical material, where the structural reconstruction by the axiomatic method has rather very slowly progressed. This means only a greater challenge, or a new area to bulldoze through, revealing new types of structures which will introduce new fusions among theories. And these breakthroughs will, in turn, mean another substantial progress in the direction of pregnant abstraction, simplification and unification, the process of which will be adapted time and again as long as maths willgo on growing.
APPENDIX III GREEK ALPHABET
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.107.243 (0.011 с.) |

 between the members of a set
between the members of a set 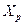 has the same structure as a relation
has the same structure as a relation  between the members of a set
between the members of a set  if there is a one-to-one correspondence between the elements of
if there is a one-to-one correspondence between the elements of  and
and  such that, whenever two elements of
such that, whenever two elements of  if a relation between the elements of
if a relation between the elements of  for any three elements
for any three elements 
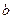
 .For example, addition of numbers is a prescription in virtue of which a third number is uniquely assigned to the sum of the first two; similarly, multiplication of numbers, addition of vectors, composition of rotations, etc., exemplify algebraic structures. Some algebraic structures belong to the second type, called structures of order; for example, the set of real numbers is ordered, since one of any two distinct real numbers is greater than the other.
.For example, addition of numbers is a prescription in virtue of which a third number is uniquely assigned to the sum of the first two; similarly, multiplication of numbers, addition of vectors, composition of rotations, etc., exemplify algebraic structures. Some algebraic structures belong to the second type, called structures of order; for example, the set of real numbers is ordered, since one of any two distinct real numbers is greater than the other.