

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Форми інфінітива та їх комунікативні значення
| Форми
| Indefinite
| Continuous
| Perfect
| Perfect- continuous
| | Active
| Passive
| Active
| Active
| Passive
| Active
| | to help
| to be helped
| to be helping
| to have helped
| to have been helped
| to have been helping
| | Приклади
| I am glad to help you.
| I am glad to be helped.
| I am glad to be helping you.
| I am glad to have helpedyou.
| I am glad to have been helped.
| I am glad to have been helpingyou for many years.
| | Я радий допомогти вам.
| Я радий, що мені допомагають.
| Я радий, що допомагаю вам (зараз).
| Я радий, що допоміг вам.
| Я радий, що мені допомогли.
| Я радий, що допомагаю вам багато років.
| | I was glad to help you.
| I was glad to be helped.
| I was glad to be helping you.
| I was glad to have helpedyou.
| I was glad to have been helped.
| I was glad to have been helping you for many years.
| | Я був радий допомогти вам.
| Я був радий, що мені допомагають.
| Я був радий, що допомагав вам (тоді).
| Я радий, що допоміг вам.
| Я радий, що мені допомогли.
| Я був радий, що допомагаю вам багато років.
| | I must help you.
| I must be helped.
| Father: Where is Pete?
Mary: He must be helpingmother in the garden.
| Father: Has anybody helped mother?
Mary: Pete must have helped her..
| Father: Has anybody helped mother?
Mary: She must have been helped.
| He must have been helpingher for many years.
| | Я повинен допомогти вам.
| Мені треба допомогти.
| Напевно, він допомагає матері в садку (зараз).
| Напевно, Піт допоміг їй.
| Напевно, їй допомогли.
| Напевно, він допомагає їй багато років.
| | Значення
| Називає дію безвідносну до часу її виконання, або дію одночасну чи майбутню по відношенню до дії, вираженої дієсловом в особовій формі.
| Називає тривалу дію, що відбувається одночасно з дією, вираженою дієсловом в особовій формі.
| Називає дію, що передує дії, вираженій дієсловом в особовій формі.
| Називає тривалу дію, що почалась раніше дії, вираженої дієсловом в особовій формі і продовжується й зараз.
|
Функції інфінітива в реченні
|
| Функція
| Приклад
| Спосіб передачі значення інфінітива українською мовою
| | 1.
| Підмет
| To read a lot is useful.
| Неозначеною формою дієслова або (рідше) іменником.
| | Читати багато – корисно.
| | 2.
| Частина складного присудка
| To read a lot is to know a lot.
| Неозначеною формою дієслова.
| | Читати багато означає знати багато.
| | We must win the game.
| | Ми повинні виграти гру.
| | I am going to enter the university.
| | Я збираюся поступати до університету.
| | 3.
| Додаток
| I want to attend this lecture.
| Неозначеною формою дієслова.
| | Я хочу відвідати цю лекцію.
| | 4.
| Означення
| Who was the first to come?
| Підрядним означальним реченням або дієсловом в особовій формі (після слів the first, the second, the last, the only, the next…).
| | Хто прийшов першим?
| | The text to be translated is difficult.
| | Текст, який потрібно перекладати, важкий.
| | 5.
| Обставина
а) мети
| You must work hard to speak English fluently.
| Неозначеною формою дієслова.
| | Ви повинні наполегливо працювати, щоб говорити англійською.
| | (In order) to speak English fluently you must work hard.
| | Для того, щоб говорити англійською, ви повинні наполегливо працювати.
| | б) наслідку
| I was too young to think of such things.
| |
| Я був занадто молодий, щоб думатипро такі речі.
|
The Infinitive Constructions
Інфінітивні звороти та їх функції у реченні.
Складний додаток /Complex Object/
Складнопідрядне додаткове речення за своїм значенням адекватне звороту “складний додаток з інфінітивом”.
| I expect that he will come here.
| I expect him to come here.
| Я сподіваюсь, що він прийде сюди.
| Зворот “складний додаток” вживається після наступних дієслів і має таку структуру:
| S
| see,
feel,
hear,
watch,
notice,
let,
make
| me
you
him
her
it
us
them
student
Mary
mother
| do
| | want,
expect,
believe,
know,
advise,
consider,
think,
like,
hate
| to do
| | order,
command,
ask (for),
allow
| to be done
| Наприклад:
| I
| saw
| him
| cross the street
| | Я
| бачив,
| як він
| переходив вулицю.
| | Mother
| wants
| Mary
| to come in time.
| | Мама
| хоче,
| щоб Мері
| прийшла вчасно.
| | We
| believe
| them
| to be honest people.
| | Ми
| віримо,
| що вони
| чесні люди.
| | The manager
| ordered
| the cargo
| to be ensured.
| | Менеджер
| наказав,
| щоб багаж
| був застрахований.
|
Складний підмет /Complex Subject/
Складно-підрядне речення з головним реченням, вираженим безособовим зворотом типу:
| it is said
| (кажуть);
| | it is reported
| (повідомляють);
| | it seems
| (здається);
| | it is likely
| (схоже);
| можна замінити простим реченням із “складним підметом”.
| It is said that they know English very well.
| They are said to know English very well.
| Кажуть, що вони добре знають англійську мову.
| Інфінітив в реченнях із “ складним підметом ” може вживатись в різних формах.
| He is said to live in Kyiv.
| Кажуть, що він живе у Києві.
| | The water seems to be boiling
| Вода, здається, кипить.
| | He was known to have lived in Kyiv.
| Відомо, що він жив у Києві.
| “ Складний підмет ” вживається, коли:
1. присудок виражений наступними дієсловами в Passive Voice:
| S+be+
| said, believed, stated, supposed, reported, thought, announced, expected, known, understood, considered, seen, heard.
| +to do
|
| This plant is known to produce tractors.
| Відомо, що цей завод виробляє трактори.
| | The delegation is reported to have left Kyiv.
| Повідомляють, що делегація поїхала з Києва.
| | He was said to have been travelling about the country a good deal.
| Говорили, що він багато подорожував по країні.
| 2. присудок виражений наступними дієсловами в Active Voice:
| S +
| seem, appear, prove, happen, chance
| + to do
| | He seems to know English well.
| Здається, він добре знає англійську
| | The weather appears to be improving.
| Погода, напевно, покращується.
| | | | | |
3. присудок виражений наступними прикметниками:
| S + be +
| likely, unlikely, certain, sure
| + to do
| | They are likely to come soon.
| Схоже, що вони скоро прийдуть.
| | The delegation is certain to arrive in Kyiv.
| Без сумніву, делегація приїде до Києва.
| | | | | |
Прийменниковий інфінітивний комплекс
(The for-to-Infinitive – Construction)
Інфінітивний комплекс може вводитися прийменником for, і називається прийменниковим інфінітивним комплексом.
| … for +
| noun
me
you
her
him
us
them
| + to do …
|
| It’s time for us to go.
| Нам пора йти.
|
Функції прийменникового інфінітивного комплексу
| Функція
| Приклади
| Спосіб передачі значення інфінітива укр. мовою.
| | 1. Складний підмет.
| For me to help you is the greatest pleasure.
Допомогти тобі – найбільше задоволення для мене.
| Інфінітивом.
| | 2. Предикатив
| It’s for you to decide.
Вирішувати це - тобі.
| Інфінітивом (з нього і починати переклад)
| | 3. Складний додаток
| We waited for the rain to stop.
Ми чекали, поки припиниться дощ.
| Іменником, складнопідрядним реченням, інфінітивом.
| | 4. Складне означення
| Here are some books for you to read.
Ось декілька книжок, які ти можеш прочитати.
| Складнопідрядним реченням; іменниковим сполученням; у деяких випадках інфінітив зовсім не перекладається.
| | 5. Складна обставина:
а) мети
| I’ve closed the window for you not to catch cold.
Я зачинив вікно, щоб ти не застудилась.
| Складнопідрядним реченням з підрядним реченням мети або наслідку.
| | б) наслідку
| You speak English too fast for me to understand.
Ти говориш занадто швидко, щоб я міг зрозуміти.
|
Text A. The Theory of Equations
Pre-text Exercises
1. Before reading the text, read the following questions. Do you know the answers already? Discuss them briefly with other students to see if they know the answers. The questions will help to give a purpose to your reading:
– Can you name all the existent number systems in English?
– Can you word mathematical formulae?
– Do you know the names of the distinguished mathematicians who contributed to the theory of equations?
2. Learn to recognize international words:
theory, history, progress, civilization, maths, evolution, review, system, complex, natural, negative, quadratic, positive, rational, irrational, real, prevail, cubic, fictitious, problem, product, symbol, term, theorem, coefficient, fundamental, algebra.
Read and translate the text:
The Theory of Equations
History shows the necessity for the invention of new numbers in the orderly progress of civilization and in the evolution of maths. We must review briefly the growth of the number system in the light of the theory of equations and see why the complex number system need not be enlarged further. Suppose we decide that we want all polynomial equations to have roots. Now let us imagine that we have no numbers in our possession except the natural numbers. Then a simple linear equation like  has no root. In order to remedy this condition, we invent fractions. But a simple linear equation, like has no root. In order to remedy this condition, we invent fractions. But a simple linear equation, like  has no root even among the fractions. Hence we invent negative numbers. A simple quadratic equation like has no root even among the fractions. Hence we invent negative numbers. A simple quadratic equation like  has no root among all the (positive and negative) rational numbers, therefore we invent the irrational numbers which together with the rational numbers complete the system of real numbers. has no root among all the (positive and negative) rational numbers, therefore we invent the irrational numbers which together with the rational numbers complete the system of real numbers.
However, a simple quadratic equation like 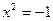 has no root among all the real numbers, hence, we invent the pure imaginary numbers. But a simple quadratic equation like has no root among all the real numbers, hence, we invent the pure imaginary numbers. But a simple quadratic equation like  has no roots among either the real or pure imaginary numbers; therefore we invent the complex numbers. The story of has no roots among either the real or pure imaginary numbers; therefore we invent the complex numbers. The story of  , the imaginary unit, and of , the imaginary unit, and of  , the complex number, originated in the logical development of algebraic theory. The word "imaginary" reflects the elusive nature of the concept for distinguished mathematicians who lived centuries ago. Early consideration of the square root of a negative number brought unvarying rejection. It seemed obvious that a negative number is not a square, and hence it was concluded that such square roots had no meaning. This attitude prevailed for a long time. , the complex number, originated in the logical development of algebraic theory. The word "imaginary" reflects the elusive nature of the concept for distinguished mathematicians who lived centuries ago. Early consideration of the square root of a negative number brought unvarying rejection. It seemed obvious that a negative number is not a square, and hence it was concluded that such square roots had no meaning. This attitude prevailed for a long time.
G. Cardano (1545) is credited with some progress in introducing complex numbers in his solution of the cubic equation, even though he regarded them as "fictitious". He is credited also with the first use of the square root of a negative number in solving the now-famous problem, "Divide 10 into two parts such that the product... is 40", which Cardano first says is "manifestly impossible"; but then he goes on to say, in a properly adventurous spirit, "Nevertheless, we will operate." Thus he found  and and  and showed that they did, indeed, have the sum of 10 and a product of 40. Cardano concludes by saying that these quantities are "truly sophisticated" and that to continue working with them is "as subtle as it is useless". Cardano did not use the symbol and showed that they did, indeed, have the sum of 10 and a product of 40. Cardano concludes by saying that these quantities are "truly sophisticated" and that to continue working with them is "as subtle as it is useless". Cardano did not use the symbol  , his designation was " , his designation was "  ", that is, "radix minus", for the square root of a negative number. R. Descartes (1637) contributed the terms "real" and "imaginary". L. Euler (1748) used " i " for ", that is, "radix minus", for the square root of a negative number. R. Descartes (1637) contributed the terms "real" and "imaginary". L. Euler (1748) used " i " for  and K. F. Gauss (1832) introduced the term "complex number". He made significant contributions to the understanding of complex numbers through graphical representation and defined complex numbers as ordered pairs of real numbers for which and K. F. Gauss (1832) introduced the term "complex number". He made significant contributions to the understanding of complex numbers through graphical representation and defined complex numbers as ordered pairs of real numbers for which
 , ,
and so forth.
Now, we may well expect that there may be some equation of degree 3 or higher which has no roots even in the entire system of complex numbers. That this is not the case was known to K. F. Gauss, who proved in 1799 the following theorem, the truth of which had long been expected: Every algebraic equation of degree n withcoefficient in the complex number system has a root (and hence n roots) among the complex numbers, later Gauss published three more proofs of the theorem. It was he who called it "fundamental theorem of algebra". Much of the work on complex number theory is Gauss'. He was one of the first to represent complex numbers as points in a plane. Actually, Gauss gave four proofs for the theorem, the last when he was seventy; in the first three proofs, he assumes, the coefficients of the polynomial equation are real, but in the fourth proof the coefficients are any complex numbers. We can be sure now that for the purpose of solving polynomial equations we do not need to extend the number system any further.
Active Vocabulary
| orderly
| регулярний, методичний
| | review
| оглядати, переглядати, передивлятися
| | briefly
| коротко, стисло
| | equation
| рівняння
| | number
| математична сума, число, цифра
| | enlarge
| збільшувати
| | further
| подальший, додатковий
| | suppose
| припускати, допускати
| | imagine
| уявляти
| | possession
| володіння
| | linear
| лінійний
| | linear equation
| рівняння першого розряду
| | root
| корінь
| | square (second) root
| квадратний корінь
| | cube (third) root
| кубічний корінь
| | in order to...
| для того, щоб...
| | remedy
| виправляти; виліковувати
| | fraction
| дріб
| | common fraction
| простий дріб; звичайний дріб
| | hence
| звідси, отже
| | the negative sign
| знак мінус
| | quadratic equation
| квадратне рівняння
| | positive sign
| знак плюс
| | real number
| дійсне число
| | therefore
| тому, отже
| | pure
| абсолютний; чистий
| | imaginary numbers
| комплексні числа
| | pure imaginary numbers
| абсолютні комплексні числа
| | оriginate
| давати початок; брати начало, виникати
| | distinguished
| видатний, відомий
| | elusive
| невловимий, ухильний
| | consideration
| розгляд, обговорення
| | vary
| змінювати(ся), міняти(ся)
| | rejection
| відмова; відхилення, неприйняття
| | obvious
| очевидний, явний
| | prevail
| мати перевагу
| | credit
| вірити, довіряти; приписувати
| | solution
| рішення, розв’язання; пояснення
| | though
| хоча, незважаючи на
| | fictitious
| вигаданий, уявний
| | product
| добуток, результат
| | manifestly
| очевидно, явно
| | properly
| належно, належним чином
| | adventurous
| нерозсудливо сміливий, заповзятливий, небезпечний, ризикований
| | nevertheless
| незважаючи на, однак, проте
| | thus
| так, у такий спосіб
| | subtle
| тонкий, невловимий
| | designation
| позначення, вказівка, призначення, мета
| | radix (pl. radices)
| корінь; мат. основа системи числення
| | contribute
| сприяти, робити внесок
| | define
| визначати
| | and so forth
| і так далі
| | degree
| ступінь, рівень
| | entire
| повний, цілий
| | it is not the case
| це не так
| | prove
| доводити
| | proof
| доказ
| | radical
| знак кореня, корінь
| | assume
| приймати на себе, привласнити
| | polynomial
| многочленний
| | polynomial equations
| багаточленні рівняння
|
|



 has no root. In order to remedy this condition, we invent fractions. But a simple linear equation, like
has no root. In order to remedy this condition, we invent fractions. But a simple linear equation, like  has no root even among the fractions. Hence we invent negative numbers. A simple quadratic equation like
has no root even among the fractions. Hence we invent negative numbers. A simple quadratic equation like  has no root among all the (positive and negative) rational numbers, therefore we invent the irrational numbers which together with the rational numbers complete the system of real numbers.
has no root among all the (positive and negative) rational numbers, therefore we invent the irrational numbers which together with the rational numbers complete the system of real numbers.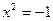 has no root among all the real numbers, hence, we invent the pure imaginary numbers. But a simple quadratic equation like
has no root among all the real numbers, hence, we invent the pure imaginary numbers. But a simple quadratic equation like  has no roots among either the real or pure imaginary numbers; therefore we invent the complex numbers. The story of
has no roots among either the real or pure imaginary numbers; therefore we invent the complex numbers. The story of  , the imaginary unit, and of
, the imaginary unit, and of  , the complex number, originated in the logical development of algebraic theory. The word "imaginary" reflects the elusive nature of the concept for distinguished mathematicians who lived centuries ago. Early consideration of the square root of a negative number brought unvarying rejection. It seemed obvious that a negative number is not a square, and hence it was concluded that such square roots had no meaning. This attitude prevailed for a long time.
, the complex number, originated in the logical development of algebraic theory. The word "imaginary" reflects the elusive nature of the concept for distinguished mathematicians who lived centuries ago. Early consideration of the square root of a negative number brought unvarying rejection. It seemed obvious that a negative number is not a square, and hence it was concluded that such square roots had no meaning. This attitude prevailed for a long time. and
and  and showed that they did, indeed, have the sum of 10 and a product of 40. Cardano concludes by saying that these quantities are "truly sophisticated" and that to continue working with them is "as subtle as it is useless". Cardano did not use the symbol
and showed that they did, indeed, have the sum of 10 and a product of 40. Cardano concludes by saying that these quantities are "truly sophisticated" and that to continue working with them is "as subtle as it is useless". Cardano did not use the symbol  , his designation was "
, his designation was "  ", that is, "radix minus", for the square root of a negative number. R. Descartes (1637) contributed the terms "real" and "imaginary". L. Euler (1748) used " i " for
", that is, "radix minus", for the square root of a negative number. R. Descartes (1637) contributed the terms "real" and "imaginary". L. Euler (1748) used " i " for  ,
,


