
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Discuss it at the students' on line conference.Содержание книги
Поиск на нашем сайте
That is as may be, the reader is no doubt thinking, but what has ali this to do with WCH or CQG? True, the second law, as it operates today, may well be part of the operation of R, but where is there any noticeable role for space-time singularities or quantum gravity in these continuing 'everyday' Imagine a sealed box of monstrous proportions. Its walls are taken to be totally reflecting and impervious to any influence. No material object may pass through, nor may any electromagnetic signal, or neutrino, or anything. All must be reflected back, whether they impinge from without or from within. Even the effects of gravity are fobidden to pass through. There is no actual substance out of which such walls could be built. No-one could actually perform the 'experiment' that I shall describe. (Nor would anyone want to, as we shall see!) That is not the point. In a thought experiment one strives to uncover general principles from the mere mental consideration of experiments that one might perform. Technological difficulties are ignored, provided they have no bearing on the general principles under consideration. In our case, the difficulties in constructing the walls for our box are to be regarded as purely 'technological' for this purpose, so these difficulties will be ignored. Inside the box is a large amount of material substance, of some kind. It does not matter much what this substance is. We are concerned only with its total mass M, which should be very large, and with the large volume V of the box which contains it. What are we to do with our expensively constructed box and its totally uninteresting contents? The experiment is to be the most boring imaginable. We are to leave it untouched – forever! The question that concerns us is the ultimate fate of the contents of the box. According to the second law of thermodynamics, its entropy should be increasing. The entropy should increase until the maximum value is attained, the material having now reached 'thermal equilibrium'. Nothing much would happen from then on, were it not for 'fluctuations' where (relatively) brief departures from thermal equilibrium are temporarily attained. In our situation, we assume that M is large enough, and V is something appropriate (very large, but not too large), so that when 'thermal equilibrium' is attained most of the material has collapsed into a black hole, with just a little matter and radiation running round it – constituting a (very cold!) so-called 'thermal bath', in which the black hole is immersed. To be definite, we could choose M to be the mass of the solar system and V to be the size of the Milky Way galaxy! Then the temperature of the 'bath' would be only about To understand more clearly the nature of this equilibrium and these fluctuations, let us recall the concept of phase space, particularly in connection with the definition of entropy. Figure 1 gives a schematic description of the whole phase space Pof the contents of Hawking's box. As we recall, a phase space is a large-dimensional space, each single point of which represents an entire possible state of the system under consideration – here the contents of the box. Thus, each point of P codifies the positions and momenta of all the particles that are present in the box, in addition to all the necessary information about the space-time geometry within the box. The subregion B(of P) on the right of Fig. 1 represents the totality of all states in which there is a black hole within the box (including all cases in which there is more than one black hole), whilst the subregion A on the left represents the totality of all states free of black holes. We must suppose that each of the regions Aand B is further subdivided into smaller compartments according to the 'coarse graining' that is necessary for the precise definition of entropy, but the details of this will not concern us here. All we need to note at this stage is that the largest of these compartments – representing thermal equilibrium, with a black hole present – is the major portion of B, whereas the (somewhat smaller) major portion of Ais the compartment representing what appears to be thermal equilibrium, except that no black hole is present.
Fig. 1. The phase space P of Hawking's box. The region A corresponds to the situations where there is no black hole in the box and B, to where there is a black hole (or more than one) in the box Recall that there is a field of arrows (vector field) on any phase space, representing the temporal evolution the physical system. Thus, to see what will happen next in our system, we simply follow along arrows in P. Some of these arrows will cross over from the region Ainto the region B. This occurs when a black hole first forms by the gravitational collapse of matter. Are there arrows crossing back again from region B into region A? Yes there are, but only if we take into account the phenomenon of Hawking evaporation. According to the strict classical theory of general relativity, black holes can only swallow things; they cannot emit things. But by taking quantum-mechanical effects into account, Hawking (1975) was able to show that black holes ought, at the quantum level, to be able to emit things after all, according to the process of Hawking radiation. (This occurs via the quantum process of 'virtual pair creation', whereby particles and anti-particles are continually being created out of the vacuum – momentarily – normally only to annihilate one another immediately afterwards, leaving no trace. When a black hole is present, however, it can 'swallow' one of the particles of such a pair before this annihilation has time to occur, and its partner may escape the hole. These escaping particles constitute Hawking's radiation.) In the normal way of things, this Hawking radiation is very tiny indeed. But in the thermal equilibrium state, the amount of energy that the black hole loses in Hawking radiation exactly balances the energy that it gains in swallowing other 'thermal particles' that happen to be running around in the 'thermal bath' in which the black hole finds itself. Occasionally, by a 'fluctuation', the hole might emit a little too much or swallow too little and thereby lose energy. In losing energy, it loses mass (by Einstein's
Fig. 2. The 'Hamiltonian flow' of the contents of Hawking's box. Flow lines crossing from A to B represent collapse to a black hole; and those from B to A, disappearance of a black hole by Hawking evaporation At this point, I should make a remark about what is meant by a 'fluctuation'. The phase-space points that belong to a single compartment are to be regarded as (macroscopically) 'indistinguishable' from one another. Entropy increases because by following the arrows we tend to get into huger and huger compartments as time progresses. Ultimately, the phase-space point loses itself in the hugest compartment of all, namely that corresponding to thermal equilibrium (maximum entropy). However, this will be true only up to a point. If one waits for long enough, the phase-space point will eventually find a smaller compartment, and the entropy will accordingly go down. This would normally not be for long (comparatively speaking) and the entropy would soon go back up again as the phase-space point re-enters the largest compartment. This is a fluctuation, with its momentary lowering of entropy. Usually, the entropy does not fall very much, but very, very occasionally a huge fluctuation will occur, and the entropy could be lowered substantially – and perhaps remain lowered for some considerable length of time. This is the kind of thing that we need in order to get from region Bto region A via the Hawking evaporation process. A very large fluctuation is needed because a tiny compartment has to be passed through just where the arrows cross over between Band A. Likewise, when our phase-space point lies inside the major compartment within A (representing a thermal equilibrium state without black holes), it will actually be a very long while before a gravitational collapse takes place and the point moves into B. Again a large fluctuation is needed. (Thermal radiation does not readily undergo gravitational collapse!) Are there more arrows leading from A to B, or from Bto A, or is the number of arrows the same in each case? This will be an important issue for us. To put the question another way, is it 'easier' for Nature to produce a black hole by gravitationally collapsing thermal particles, or to get rid of a black hole by Hawking radiation, or is each as 'difficult' as the other? Strictly speaking it is not the 'number' of arrows that concerns us, but the rate of flow of phase-space volume. Think of the phase space as being filled with some kind of (high-dimensional!) incompressible fluid. The arrows represent the flow of this fluid. Recall Liouville's theorem. Liouville's theorem asserts that the phase-space volume is preserved by the flow, which is to say that our phase-space fluid is indeed incompressible! Liouville's theorem seems to be telling us that the flow from Ato Bmust be equal to the flow from B to Abecause the phase-space 'fluid', being incompressible, cannot accumulate either on one side or the other. Thus it would appear that it must be exactly equally 'difficult' to build a black hole from thermal radiation as it is to destroy one! This, indeed, was Hawking's own conclusion, though he came to this view on the basis of somewhat different considerations. Hawking's main argument was that all the basic physics that is involved in the problem is time-symmetrical (general relativity, thermodynamics, the standard unitary procedures of quantum theory), so if we run the clock backwards, we should get the same answer as if we run it forwards. This amounts simply to reversing the directions of all the arrows in P. It would then indeed follow also from this argument that there must be exactly as many arrows from Ato Bas from B to In any case, the suggestion is not really compatible with the ideas that I am putting forward here. I have argued that whereas black holes ought to exist, white holes are forbidden because of the Weyl curvature hypothesis! WCH introduces a time-asymmetry into the discussion which was not considered by Hawking. It should be pointed out that since black holes and their space-time singularities are indeed very much part of the discussion of what happens inside Hawking's box, the unknown physics that must govern the behaviour of such singularities is certainly involved. Hawking takes the view that this unknown physics should be a time-symmetric quantum gravity theory, whereas I am claiming that it is the time-flasymmetric CQG! I am claiming that one of the major implications of COG should be WCH (and, consequently, the second law of thermodynamics in the form that we know it), so we should try to ascertain the implications of WCH for our present problem. Let us see how the inclusion of WCH affects the discussion of the flow of our 'incompressible fluid' in P. In space-time, the effect of a black-hole singularity is to absorb and destroy all the matter that impinges upon it. More importantly for our present purposes, it destroys information. The effect of this, in P, is that some flow lines will now merge together (see Fig. 3). Two states which were previously different can become the same as soon as the information that distinguishes between them is destroyed. When flow lines in Pmerge together we have an effective violation of Liouville's theorem. Our 'fluid' is no longer incompressible, but it is being continually annihilated within region B!
Fig. 3. In region B flow lines must come together because of information loss at black-hole singularities. Is this balanced by a creation of flow lines due to the quantum procedure R (primarily in region A)? Now we seem to be in trouble. If our 'fluid' is being continually destroyed in region B, then there must be more flow lines from Ato B than there are from B to A – so it is 'easier' to create a black hole than to destroy one after all! This could indeed make sense were it not for the fact that now more 'fluid' flows out of region A than re-enters it. There are no black holes in region A – and white holes have been excluded by WCH – so surely Liouville's theorem ought to hold perfectly well in region A! However, we now seem to need some means of 'creating fluid' in region A to make up the loss in region B. What mechanism can there be for increasing the number of flow lines? What we appear to require is that sometimes one and the same state can have more than one possible outcome (i.e. bifurcating flow lines). This kind of uncertainty in the future evolution of a physical system has the 'smell' of quantum theory about it – the R part. Can it be that R is, in some sense, 'the other side of the coin' to WCH? Whereas WCH serves to cause flow lines to merge within B, the quantum-mechanical procedure R causes flow lines to bifurcate. I am indeed claiming that it is an objective quantum-mechanical process of state-vector reduction (R) which causes flow lines to bifurcate, and so compensate exactly for the merging of flow lines due to WCH (Fig. 3)! In order for such bifurcation to occur, we need R to be time-asymmetric, as we have already seen: recall our experiment above, with the lamp, photo-cell, and half-silvered mirror. When a photon is emitted by the lamp, there are two (equally probable) alternatives for the final outcome: either the photon reaches the photo-cell and the photo-cell registers, or the photon reaches the wall at A and the photo-cell does not register. In the phase space for this experiment, we have a flow line representing the emission of the photon and this bifurcates into two: one describing the situation in which the photo-cell fires and the other, the situation in which it does not. This appears to be a genuine bifurcation, because there is only one allowed input and there are two possible outputs. The other input that one might have had to consider was the possibility that the photon could be ejected from the laboratory wall at B, in which case there would be two inputs and two outputs. But this alternative input has been excluded on the grounds of inconsistency with the second law of thermodynamics – i.e. from the point of view expressed here, finally with WCH, when the evolution is traced into the past. I should re-iterate that the viewpoint that I am expressing is not really a 'conventional' one – though it is not altogether clear to me what a 'conventional' physicist would say in order to resolve all the issues raised. (I suspect that not many of them have given these problems much thought!) I have Finally, there is a serious point that I have glossed over. I started the discussion by assuming that we had a classical phase space – and Liouville's theorem applies to classical physics. But then the quantum phenomenon of Hawking radiation needed to be considered. (And quantum theory is actually also needed for the finite-dimensionality as well as finite volume of P). As we saw, the quantum version of phase space is Hilbert space, so we should presumably have used Hilbert space rather than phase space for our discussion throughout. In Hilbert space there is an analogue of Liouville's theorem. It arises from what is called the 'unitary' nature of the time-evolution U. Perhaps my entire argument could be phrased entirely in terms of Hilbert space, instead of classical phase space, but it is difficult to see how to discuss the classical phenomena involved in the space-time geometry of black holes in this way. My own opinion is that for the correct theory neither Hilbert space nor classical phase space would be appropriate, but one would have to use some hitherto undiscovered type of mathematical space which is intermediate between the two. Accordingly, my argument should be taken only at the heuristic level, and it is merely suggestive rather than conclusive. Nevertheless, I do believe that it provides a strong case for thinking that WCH and R are profoundly linked and that, consequently, R must indeed be a quantum gravity effect. To re-iterate my conclusions: I am putting forward the suggestion that quantum-mechanical state-vector reduction is indeed the other side of the coin to WCH. According to this view, the two major implications of our sought-for 'correct quantum gravity' theory (CQG) will be WCH and R. The effect of WCH is confluence of flow lines in phase space, while the effect of R is an exactly compensating spreading of flow lines. Both processes are intimately associated with the second law of thermodynamics. Note that the confluence of flow lines takes place entirely within the region B, whereas flow-line spreading can take place either within A or within B. Recall that Arepresents the absence of black holes, so that state-vector reduction can indeed take place when black holes are absent. Clearly it is not necessary to have a black hole in the laboratory in order that R be effected (as with our experiment with the photon, just considered). We are concerned here only with a general overall balance between possible things which might happen in a situation. On the view that I am expressing, it is merely the possibility that black holes might form at some stage (and consequently then destroy information) which must be balanced by the lack of determinism in quantum theory! APPENDIX II 1. Study all the texts, collect information and write two-pages-long compositions on each of the following topics: 1. The Founders of Number Theory. 2. Number Theory. 3. Modern Number Systems and Concepts. 4. Natural Numbers. 5. Real Numbers. 6. Structures. 2. The following questions may direct you: 1. What are the stages of Number Theory evolution during the past 2300 years? 2. What new methods are basic nowadays for the Number Theory? 3. What are your critical comments on Modern Number Systems and Concepts? 4. Why are Natural Numbers one of the basic and most essential Concept of Maths? 5. What was the evolution of Real Numbers from the Babylonians till nowadays? 6. Are there any theories with their Structures entirely indeterminate?
|
|||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.008 с.) |




 occurrences state-vector reduction? In order to address this question, I wish to describe an outlandish 'thought experiment', originally proposed by Stephen Hawking, though the purpose to which it will be put is not part of what Hawking had originally intended.
occurrences state-vector reduction? In order to address this question, I wish to describe an outlandish 'thought experiment', originally proposed by Stephen Hawking, though the purpose to which it will be put is not part of what Hawking had originally intended. of a degree above absolute zero!
of a degree above absolute zero!
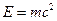 ) and, according to the rules governing Hawking radiation, it gets a tiny bit hotter. Very very occasionally, when the fluctuation is large enough, it is even possible for the black hole to get into a runaway situation whereby it grows hotter and hotter, losing more and more energy as it goes, getting smaller and smaller until finally it (presumably) disappears completely in a violent explosion! When this happens (and assuming there are no other holes in the box), we have the situation where, in our phase space P, we pass from region Bto region A, so indeed there are arrows from Bto A!
) and, according to the rules governing Hawking radiation, it gets a tiny bit hotter. Very very occasionally, when the fluctuation is large enough, it is even possible for the black hole to get into a runaway situation whereby it grows hotter and hotter, losing more and more energy as it goes, getting smaller and smaller until finally it (presumably) disappears completely in a violent explosion! When this happens (and assuming there are no other holes in the box), we have the situation where, in our phase space P, we pass from region Bto region A, so indeed there are arrows from Bto A!



 A provided that it is the case that the time-reverse of the region Bis the region Bagain (and, equivalently, that the time-reverse of A is A again). This proviso amounts to Hawking's remarkable suggestion that black holes and their time-reverses, namely white holes, are actually physically identical! His reasoning was that with time-symmetric physics, the thermal equilibrium state ought to be time-symmetric also. I do not wish to enter into a detailed discussion of this striking possibility here. Hawking's idea was that somehow the quantum-mechanical Hawking radiation could be regarded as the time-reverse of the classical 'swallowing' of material by the black hole. Though ingenious, his suggestion involves severe theoretical difficulties, and I do not myself believe that it can be made to work.
A provided that it is the case that the time-reverse of the region Bis the region Bagain (and, equivalently, that the time-reverse of A is A again). This proviso amounts to Hawking's remarkable suggestion that black holes and their time-reverses, namely white holes, are actually physically identical! His reasoning was that with time-symmetric physics, the thermal equilibrium state ought to be time-symmetric also. I do not wish to enter into a detailed discussion of this striking possibility here. Hawking's idea was that somehow the quantum-mechanical Hawking radiation could be regarded as the time-reverse of the classical 'swallowing' of material by the black hole. Though ingenious, his suggestion involves severe theoretical difficulties, and I do not myself believe that it can be made to work.

 certainly heard a number of differing points of view. For example, it has from time to time been suggested, by some physicists, that Hawking radiation would never completely cause a black hole to disappear, but some small 'nugget' would always remain. (Hence, on this view, there are no arrows from B to A)! This really makes little difference to my argument (and would actually strengthen it). One could evade my conclusions, however, by postulating that the total volume of the phase-space Pis actually infinite, but this is at variance with certain rather basic ideas about black-hole entropy and about the nature of the phase space of a bounded (quantum) system; and other ways of technically evading my conclusions that I have heard of seem to me to be no more satisfactory. A considerably more serious objection is that the idealizations involved in the actual construction of Hawking's box are too great, and certain issues of principle are transgressed in assuming that it can be built. I am uncertain about this myself, but I am inclined to believe that the necessary idealizations can indeed be swallowed!
certainly heard a number of differing points of view. For example, it has from time to time been suggested, by some physicists, that Hawking radiation would never completely cause a black hole to disappear, but some small 'nugget' would always remain. (Hence, on this view, there are no arrows from B to A)! This really makes little difference to my argument (and would actually strengthen it). One could evade my conclusions, however, by postulating that the total volume of the phase-space Pis actually infinite, but this is at variance with certain rather basic ideas about black-hole entropy and about the nature of the phase space of a bounded (quantum) system; and other ways of technically evading my conclusions that I have heard of seem to me to be no more satisfactory. A considerably more serious objection is that the idealizations involved in the actual construction of Hawking's box are too great, and certain issues of principle are transgressed in assuming that it can be built. I am uncertain about this myself, but I am inclined to believe that the necessary idealizations can indeed be swallowed!


