
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
What is the very essence of mathematical visualization? Key-words: magnification, abstract mathematics, complex numbers, miracles of mathematics.Содержание книги
Поиск на нашем сайте
We are now in a position to see how the Mandelbrot set is defined. Let
where с is another fixed (i.e. given) complex number. The number
so that, in particular, 3 would be replaced by
and
When such numbers get complicated, the calculations are best carried out by an electronic computer. Now, whatever с may be, the particular number 0 is replaced, under this scheme, by the actual given number
Let us iterate the replacement again, applying it next to the above number to obtain
and then again to this number, and so on. We obtain a sequence of complex numbers, starting with 0:
Now if we do this with certain choices of the given complex number c, the sequence of numbers that we get in this way never wanders very far from the origin in the Argand plane; more precisely, the sequence remains bounded for such choices of с which is to say that every member of the sequence lies within some fixed circle centred at the origin (see Fig. 1). A good example where this occurs is the case
Fig. 1. A sequence of points in the Argand plane is bounded if there is some fixed circle that contains all the points. (This particular iteration starts with zero and has in this case, every member of the sequence is in fact 0. Another example of bounded behaviour occurs with
The Mandelbrot set, that is to say, the black region of our world of Tor'Bled-Nam, is precisely that region of the Argand plane consisting of points The complexity of the Mandelbrot set is very remarkable, particularly in view of the fact that the definition of this set is, as mathematical definitions go, a strikingly simple one. It is also the case that the general structure of this set is not very sensitive to the precise algebraic form of the mapping
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.006 с.) |

 be some arbitrarily chosen complex number. Whatever this complex number is, it will be represented as some point on the Argand plane. Now consider the mapping whereby
be some arbitrarily chosen complex number. Whatever this complex number is, it will be represented as some point on the Argand plane. Now consider the mapping whereby  ,
, will be represented by some new point in the Argand plane. For example, if
will be represented by some new point in the Argand plane. For example, if  happened to be given as the number
happened to be given as the number 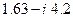 , then
, then 

 would be replaced by
would be replaced by
 Suppose we continue this process and apply the replacement to the number
Suppose we continue this process and apply the replacement to the number  .
.
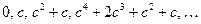
 , since
, since
 ).
). , for then the sequence is:
, for then the sequence is:  ; and yet another example occurs with
; and yet another example occurs with  , the sequence being
, the sequence being  . However, for various other complex numbers с the sequence wanders farther and farther from the origin to indefinite distance; i.e. the sequence is unbounded, and cannot be contained within any fixed circle. An example of this latter behaviour occurs when
. However, for various other complex numbers с the sequence wanders farther and farther from the origin to indefinite distance; i.e. the sequence is unbounded, and cannot be contained within any fixed circle. An example of this latter behaviour occurs when  , for then the sequence is
, for then the sequence is  ; this also happens when
; this also happens when  , the sequence being
, the sequence being  ; and also when
; and also when  , the sequence being
, the sequence being .
. and decide, according to some appropriate criterion, whether the sequence is remaining bounded or not. If it is bounded, then the computer would arrange that a black spot appear on the screen at the point corresponding to с. If it is unbounded, then the computer would arrange for a white spot. Eventually, for every pixel in the range under consideration, the decision would be made by the computer as to whether the point would be coloured white or black.
and decide, according to some appropriate criterion, whether the sequence is remaining bounded or not. If it is bounded, then the computer would arrange that a black spot appear on the screen at the point corresponding to с. If it is unbounded, then the computer would arrange for a white spot. Eventually, for every pixel in the range under consideration, the decision would be made by the computer as to whether the point would be coloured white or black. that we have chosen. Many other iterated complex mappings (e.g.
that we have chosen. Many other iterated complex mappings (e.g.  ) will give extraordinarily similar structures (provided that we choose an appropriate number to start with – perhaps not 0, but a number whose value is characterized by a clear mathematical rule for each appropriate choice of mapping). There is, indeed, a kind of universal or absolute character to these 'Mandelbrot' structures, with regard to iterated complex maps. The study of such structures is a subject on its own, within mathematics, which is referred to as complex dynamical systems.
) will give extraordinarily similar structures (provided that we choose an appropriate number to start with – perhaps not 0, but a number whose value is characterized by a clear mathematical rule for each appropriate choice of mapping). There is, indeed, a kind of universal or absolute character to these 'Mandelbrot' structures, with regard to iterated complex maps. The study of such structures is a subject on its own, within mathematics, which is referred to as complex dynamical systems.


