
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Number Theory and its FoundersСодержание книги
Поиск на нашем сайте
Mathematics is the Queen of Science and Arithmetic is the Queen of Mathematics. Gauss. The theory of numbers, one of the oldest branches of maths, has engaged the attention of many gifted mathematicians during the past 2300 years. The Greeks, Indians and Chinese had made significant contributions prior to 1000 A.D. and in more modern times the subject has been developed steadily since Fermat, one of the fathers of maths. In view of the diversity of problems and methods grouped together under the name of number theory, it is impossible to write even an introductory treatment which in any sense covers the field completely. The properties of the series of natural numbers, one of the basic and most essential concepts of maths, are the object of the theory of numbers. One finds that there exist many simple rules regarding numbers that are quite easy to discover and not too difficult to prove. However, number theory also includes an abundance of problems whose content can be comprehended and expressed in simple terms, yet whose solution has for centuries defied all math investigation. Other problems whose solutions have been successfully obtained have yielded only to attacks by some of the most ingenious and advanced methods of modern maths. The simplicity in form of its problems and the great variation in the methods and tools for their solution explain the attraction that number theory has had for mathematicians and laymen. The innumerable individual contributions, calculations, speculations, and conjectures bear witness to the continued interest in this field of maths throughout the centuries. The origins of the study of number properties go back probably almost as far as counting and the arithmetic operations. It does not take long before it is discovered that some numbers behave differently from the others; for instance, some numbers can be divided into smaller equal parts and others not. The operations with fractions lead immediately to the study of divisibility of numbers, the least common multiple, and the greatest common divisor. Other approaches have led to early number-theory questions. In number theory we are concerned with properties of certain of the integers..., -3, -2, -1, 0, 1, 2, 3,..., or sometimes with those properties of the real and complex numbers which depend rather directly on the integers. As in most branches of abstract thought, it is easier to characterize the theory of numbers extensively, by giving a large number of examples of problems which are usually considered as parts of number theory, than to define it intensively, by saying that exactly those problems having certain characteristics will be included in the subject. The problems treated in classical number theory can be divided into groups according to a more or less rough classification. First, there are multiplicative problems, concerning with divisibility properties of the integers. It will be proved later that any positive integer n greater than 1 can be represented uniquely except for the order of the factors, as a product of primes, i.e., integers greater than 1 having no exact divisors except itself and 1. This may also be termed the fundamental theorem of number theory so manifold and varied are its applications. From the decomposition of In another direction, we have the problems of additive number theory: questions concerning the representability, and the number of representations of a positive integer as a sum of integers of a specified kind. For instance, upon examination it appears that some integers, like A third category may include what are known as Diophantine equations named after the Greek mathematician Diophantus, who first studied them. These are equations in one or more variables whose solutions must be integers, or at any rate rational numbers. For example, it is a familiar fact that Finally, there are problems in Diophantine approximations. For example, given a real number The theorems of number theory can also be subdivided along entirely different lines – for example, according to the methods used in their proofs. Thus, the dichotomies of elementary and nonelementary, analytic and synthetic. A proof is elementary (although not necessarily simple!) if it makes no use of the theory of functions of a complex variable, and synthetic if it does not involve the usual concepts of analysis – limits, continuity, etc. Sometimes, but not always, the nature of the theorem shows that the proof will be in one or another of these categories. Pierre de Fermat P. Fermat (1601-1665) must be awarded the honour of being the founding father of number theory as a systematic science. His life was quiet and uneventful and entirely centred around the town of Toulouse, where he first studied jurisprudence, practised law, and later became prominent as councillor of the local parliament. His leisure time was devoted to scholary pursuits and to a voluminous correspondence with contemporary mathematicians, many of whom, like himself, were gentlemen-scholars, the ferment of intellectual life in the seventeenth and eighteenth centuries. Fermat possessed a broad knowledge of the classics, enjoyed literary studies, and wrote verse, but maths was his real love! He published practically nothing personally, so that his works have been gleaned from notes that were preserved after his death by his family, and from letters and treatises that he had sent to his correspondents. In spite of his modesty, Fermat gained an outstanding reputation for his math achievements. He made considerable contributions to the foundation of the theory of probability in his correspondence with Pascal and introduced coordinates independently of Descartes. The French often interject the name of Fermat as a cofounder of the calculus, and there is considerable justification for this point of view. In spite of all these achievements, Fermat's real passion in maths was undoubtebly number theory. He returned to such problems in almost all his letters; he delighted to propose new and difficult problems, and to give solutions in large figures that require elaborate computations; and most important of all, he announced new principles and methods that have inspired all work in number theory after him. Fermat's factorization method (which is the point interesting us particularly) is based upon the following facts. If a number
On the other hand, if
Since we deal with the question of factoring Since Fermat's method is particularly helpful when the number Of particular interest is Fermat's last theorem. Greek maths, as is known, was geometric in character. However, during the later Alexandrian period, the algebraic methods came more into the foreground. During this period, Diophantus (A.D. 250), the most renowned proponent of Greek algebra, lived in Alexandria. Nothing is known about his life. All his books deal with the properties of rational and integral numbers, topics on algebraic equations and more particularly with the solution of certain problems in which it is required to find rational numbers satisfying prescribed conditions. More than 130 problems of this latter type are discussed, and Diophantus shows great ingenuity in devising elegant methods for their solution. The path from Diophantus to Fermat although long in time, is quite direct. Fermat represents a focal point in the history of number theory; in his work the radiating branches of earlier periods were united and their content recreated in a richer and more systematic form. Fermat possessed a well-known copy of Diophantus, which he also used as a notebook. In the margins he jotted down several of his most important remarks as they occurred to him in connection with the related problems in Diophantus. We now come to the most famous of Fermat's remarks in his copy of Diophantus. In problem 8 in Book II Diophantus propounds: "To decompose a given square number into the sum of two squares. " To use a general notation, let This problem to us is quite straightforward, but it was not always so. In the oldest preserved Diophantus' manuscript, copied in the thirteenth century we find at this point the following heartfelt remark by the writer: "Thy soul, Diophantus, to Satanas, for the difficulty of thy problems and this one in particular." Fermat's comments in connection with this problem are as one should expect considerably more constructive and of much greater consequence: "However, it is impossible to write a cube as the sum of two cubes, a fourth power as the sum of two fourth powers and in general any power beyond the second as the sum of two similar powers. For this I have discovered a truly wonderful proof, but the margin is too small to contain it." This is the famous Fermat's theorem, sometimes called Fermat's last theorem, on which the most prominent mathematicians have tried their skill ever since its announcement three hundred years ago. In algebraic language, it requires that it shall be shown that the Diophantine equation Fermat's problem has remained remarkably active throughout its history, and results and research on it still appear frequently in the math journals. It must be admitted frankly that if the specific result implied in the theorem were obtained, it would, probably, have little systematic significance for the general progress of maths. However, the theorem has been extremely important as a goal and a constant source of new efforts. Some of the new methods it has inspired are basic nowadays not only for number theory but also for many other branches of maths. Leonhard Euler Leonhard Euler (1707-1783) was a remarkable scientist whose contributions have left their imprint on almost all branches of maths. His papers were rewarded ten times by prizes of the French Academy. His productivity was immense; it has been estimated that his collected works fill upward of 100 large volumes. One of his best known works Complete Introduction to Algebra (1770) contains much material on elementary number theory. Euler's factorization method applies only to numbers which in some way can be represented as a sum of two squares Such representations can under certain conditions be used for factoring in the same manner as the special form It will carry us too far to discuss the great number of other aids and methods for factoring, some of them very ingenious. Considerable effort has been centred on the factorization of numbers of particular types. Some of them are numbers resulting from math problems of interest. Others have been selected because it is known for theoretical reasons that the factors must have a special form. Among the numbers that have been examinated in great detail one should mention the so-called binomial numbers
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 603; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.207 (0.007 с.) |

 into primes, it is easy to determine the number of divisors of
into primes, it is easy to determine the number of divisors of 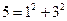 and
and 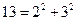 , are representable as a sum of two squares; while others, like 3 or 12, are not. Which integers are so representable and how many such representations are there?
, are representable as a sum of two squares; while others, like 3 or 12, are not. Which integers are so representable and how many such representations are there? which gives us a solution of the Diophantine equation
which gives us a solution of the Diophantine equation 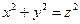 . Giving a particular solution is hardly of interest; what is desired is an explicit formula for absolutions. A very famous Diophantine equation is that known as Fermat's equation:
. Giving a particular solution is hardly of interest; what is desired is an explicit formula for absolutions. A very famous Diophantine equation is that known as Fermat's equation: 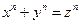 . Fermat asserted that this equation has no solution (in nonzero integers, of course) if
. Fermat asserted that this equation has no solution (in nonzero integers, of course) if  ; the assertion has never been proved or disproved for general
; the assertion has never been proved or disproved for general  and a positive integer
and a positive integer  , find that rational number
, find that rational number  for which
for which  and
and 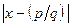 is minimal. The proofs that
is minimal. The proofs that  and
and 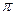 are transcendental also fall in this category. This branch of number theory probably borrows the most from, and contributes the most to, other branches of maths.
are transcendental also fall in this category. This branch of number theory probably borrows the most from, and contributes the most to, other branches of maths. (1)
(1) ,
,  is composite, one can obtain a representation (1) of
is composite, one can obtain a representation (1) of  ,
,  sothat
sothat ,
, 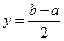 (2)
(2) and
and 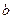 are odd and the values of
are odd and the values of  are integral. Corresponding to eachfactorization of
are integral. Corresponding to eachfactorization of  .
. , one has
, one has  . The procedure consists in substituting successively for
. The procedure consists in substituting successively for  and examining whether the corresponding,
and examining whether the corresponding, 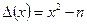 is a square
is a square 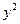 .
. is relatively small, because a suitable у will then quickly appear. By means of certain other improvements that can be introduced in the procedure, it becomes one of the most effective factorization methods available.
is relatively small, because a suitable у will then quickly appear. By means of certain other improvements that can be introduced in the procedure, it becomes one of the most effective factorization methods available. be the given square for which one wants to find
be the given square for which one wants to find 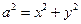 . As usual, Diophantus asks for rational solutions.
. As usual, Diophantus asks for rational solutions. , all different from zero, when
, all different from zero, when  as, for instance,
as, for instance, 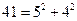 . It is possible to show that if a number can be represented as the sum of two squares, one can find all factorizations by Euler's method. Euler's method is capable of wide extensions. It leads to the theory of representations of numbers by means of a quadratic forms, i.e.,
. It is possible to show that if a number can be represented as the sum of two squares, one can find all factorizations by Euler's method. Euler's method is capable of wide extensions. It leads to the theory of representations of numbers by means of a quadratic forms, i.e.,  .
.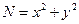 .
. where
where 


