
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Georg Friedrich Bernhard RiemannСодержание книги
Поиск на нашем сайте
Although Euler had begun applying the methods of the calculus to number-theory problems, however, the German mathematician G. F. B. Riemann (1826-1866) is generally regarded as the real founder of analytic number theory. His personal life was modest and uneventful until his premature death from tuberculosis. According to the wish of his father he was originally destined to become a minister, but his shyness and lack of ability as a speaker made him abandon this plan in favour of math scholarship. At present he is recognized as one of the most penetrating and original math minds of the nineteenth century. In analytic number theory, as well as in many other fields of maths, his ideas still have a profound influence. His starting point was a function now called Riemann's zeta function
This function he investigated in great detail and showed that its properties are closely connected with the prime-number distribution. On the basis of Riemann's ideas, the prime-number theorems were proved by other mathematicians. Much progress has been made in analytic number theory since that time, but it remains a peculiar fact that the key to some of the most essential problems lies in the so-called Riemann's hypothesis, the last of his conjectures about the zeta function, which has not been demonstrated. It states that the complex roots of the function all have the real component
Active Vocabulary
The Greek Genius "The Greek genius" did not happen spontaneously. Once the Greeks were settled in the Peloponesus and on the western shores of Asia Minor, they began to travel. Soon they were off the faraway places. On these travels they made contact with many more ancient cultures – in India, in Mesopotamia, and in Egypt. They learned and partially absorbed ways of life that had taken thousands of years to develop. Knowledge, wisdom and religion often were indistinguishable in these ancient cultures. What the early Greek travellers brought home from their trips abroad was a curious and intricate mixture of various religious cults and philosophies of life grown under conditions very different from those familiar to the Greeks. They accumulated also a tremendous wealth of knowledge pertaining to practically all aspects of life. Deeply woven into it all was knowledge of numeration and number, astronomy and (as we would call it now) astrology, and an abundance of geometric patterns and designs. It may be supported that the early Greeks were not very much interested in numeration – if, indeed, they were interested in it at all. This was true in spite of the infinite contact with positional numeration systems, like those of Babylonians, which were vastly superior in design and manageability to their own nonpositional numeration system. Their minds apparently were not inclined toward the mechanical and rote aspects of elementary maths but rather were fascinated by suspected underlying reasons and possible justifications. The Pythagoreans did not refine and propagandize numeration but concentrated – aside from their magnificent work in geometry – on studying the properties of numbers, in particular, the positive integers. They, thereby, missed or knowingly passed by the much more significant study of the properties of operations on numbers, which might have led them to create a structure of number systems similar to that which they created for geometry. To appreciate the preoccupation of the Pythagoreans with properties of numbers, we must keep two things in mind: 1) The Greeks had inherited from the earlier Eastern cultures an almost inextricable mixture of genuine number knowledge, myths, religious beliefs; 2) The prevailing numeration system of this period made use of the standard Greek alphabet supplemented by special symbols so as to make a set of twenty-seven characters. Although there was no difficulty in determining when the symbols represented a number instead of a word, it was possible to use the numerical value of each letter to assign a unique number to any given word. Regardless of what mystical reasons may have motivated the early Pythagorean investigators, they discovered many curious and fascinating number properties. Since the general Greek outlook toward maths was more geometric than in arithmetical, and since in their earlier work the Greeks considered only whole numbers, it is no wonder that they attempted to represent numbers as geometric patterns. The Greeks' concern with prime numbers was considerably deeper and more serious. It was known that, with the exception of one and two, any whole number that is not prime can be expressed as a product of primes. The Greeks not only formalized these findings but established what later became known as "the fundamental theorem of arithmetic" – namely, that a composite number can be expressed as a product of primes in one and only one way. This theorem is known as the "unique factorization theorem". Euclid presented a proof in his Elements to show that the set of prime numbers is infinite – that is, that there is no greatestprime. In spite of many attempts so far, no one has been able to devise a practicaltest for checking the primality of large numbers, nor has a truly general prime generator been discovered. With due respect to a very few isolated Greek mathematicians, it must be pointed out that the only numbers accepted by Greeks were the natural numbers. The foremost of these few mathematicians was Eudoxus (408-355 B.C.). He showedthat the measure of the diagonal of the unit square could not be expressed as the ratio of two natural numbers, that is, that the symbol To most of the Greek mathematicians the very idea of incommensurable quantities was disagreeable and fearful. Eudoxus' theory of equal ratios was soon discarded and forgotten. More than two thousand years elapsed before the German mathematicians Dedekind and Cantor took up the work where Eudoxus had left off and brought it to completion creating the real number system and thereby, a legitimate "place" for imaginary and complex numbers. Thus, the "Greek genius" was no more concerned with number systems than with numerational systems. While the math contributions of many ancient cultures were numeration, a principal Greek contribution was arithmetic, knowledge of the properties of numbers. The modern approach is definitely oriented toward the structural properties of number systems (not of numeration systems) – that is, toward the patterns and properties of operations on numbers which provide unity, simplicity, and continuity from the system of the whole numbers through the system of the complex numbers. Natural Numbers What are natural numbers? The question has been a topic of debate among philosophers and mathematicians at least since the time of Pythagoras in the sixth century B.C. Pythagoras believed that what we call the positive integers or natural numbers (1,2,3 and so on) were God-given entities that formed the ultimate foundation both of maths and of the Universe. The Pythagoreans' own discovery of such "incommensurable" quantities as the ratio between the diameter of a circle and its circumference ultimately dispelled the belief that the Universe was built on natural numbers. That the natural numbers provided the foundation of maths, however, persisted as an article of faith among mathematicians until well into the 19th century. But then the attitude toward the natural numbers had begun to change. The centrality of natural numbers was no longer considered an accepted fact but was viewed as a conjecture that required rigorous proof. The proofs usually took the form of a stepwise derivation of such well-known number systems as rational, real and complex numbers from the natural numbers themselves. Two examples are the attempts of K.Weierstrass and R. Dedekind to "arithmetize" math analysis. Both scholars derived real numbers – the combined set of all rational and irrational numbers that is employed in most classical maths – from the rational numbers. A third example is the proposal of L.Kronecker to found all maths on the natural numbers. This Kronecker attempted to accomplish solely with "finitary" methods, that is, methods invoking neither nonfinite entities nor proofs involving more than a finite number of steps. Still other mathematicians, in particular those who were conversant with contemporary advances in symbolic logic, put forward the suggestion that, far from being God-given, natural numbers were constructions of the human mind. The three most famous propagators of this suggestion were G.Frege, G.Peano and B.Russell. Obviously a theory was needed that would trace the rise of the natural numbers from some more basic notion or notions, but how was such a theory to be constructed? If most or all of classical maths had evolved from the natural numbers, it was improbable that the required theory could be devised entirely within the bounds of classical maths. First Frege, then Peano and finally Russell turned to symbolic logic as a potential source of the fundamental notions necessary for a theory of natural numbers. Frege was the first of the three to publish specific theory (1884) in which he proposed that the natural numbers could be reduced to the notion of "class" and the operation of "correspondence", by virtue of which classes are quantified. According to Frege, each natural number In essence, Frege's theory states that the series of natural numbers presents a general problem of quantification, but that the general problem can be reduced to the more restricted notion of "cardination" or quantifying classes. The commonest example of cardination is the matching of things. Frege's cardinal theory remained unknown until Russell rediscovered it in 1901. Russell subsequently published the cardinal theory, with full acknowledgement to Frege, in his own works and in his joint work with A.N. Whitehead: Principia Mathematica (1910-1913). Between the time Frege first published the cardinal theory and the time Russell rediscovered it, Peano developed a second theory about the natural numbers. This theory first appeared in 1894 in the form of five axioms, that we shall slightly reword here. First, 1 is a natural number. Second, any number that is the successor of a natural number is itself a natural number. Third, no two natural numbers have the same successor. Fourth, the natural number 1 is not the successor of any natural number. Fifth, if a series of natural numbers include both the number 1 and the successor of every natural number, then the series contains all natural numbers. In essence, Peano's theory places the natural numbers in an ordinal relation or in the language of symbolic logic, a "transitive, asymmetrical relation". If we are willing to stipulate that the relation R that obtains between every nonidentical pair of natural numbers be an ordinal relation, then the complete series of natural numbers can be constructed stepwise with the aid of the rule of math induction. Like Frege's cardinal theory, Peano's states that the series of natural numbers presents a general problem of quantification. Unlike Frege's theory, however, Peano's ordinal theory reduces the general problem to the more restricted notion of quantifying transitive, asymmetrical relations, or ordination. The commonest example of ordination is the counting of things. Just which of the two theories, the cardinal or the ordinal, is mathematically preferable is a question that has never been answered to everyone's satisfaction. Reasonable objections can be lodged against both. For example, the cardinal theory is subject to the celebrated paradox, discovered by Russell in 1901, concerning the class composed of all those classes that are not members of themselves. With respect to the ordinal theory, as Russell pointed out, whereas Peano's five axioms obviously are satisfied by the series of natural numbers, they are equally satisfied by other number systems. For example, the rational fractions (1, Because there is no universally accepted math basis for choosing between the cardinal and the ordinal theories, the choice becomes a subjective matter. Typically, the choice is determined by one's degree of sympathy with one or another of three modern schools of math thought: logicism, formalism and intuitionism. Those who lean toward logicism, favour the cardinal theory, a choice that is natural enough when one considers that the codiscoverers of the theory, Frege and Russell, were the principal founders of logicism. Those whose sympathies are with formalism, lean toward the ordinal theory; the fact that Peano's axioms seem to denude the number concept of innate "meaning" probably explains this preference. As for the intuitionists, they have, in effect, returned to the Pythagorean position that the natural numbers must be accepted without further analysis as the foundation of maths. They deny that the natural numbers are the invention of math minds and offer a "psychological" thesis: The series of natural numbers is an innate intuition, present at birth in all normal members of the human species. Nonmath scholars tend to view with profound indifference the tortures that mathematicians suffer over such basic issues as the nature of number. They have learned from centuries of hard experience that the mere fact that the foundations of some math system or concept are not secure need not deter them from employing the system in their work. On the contrary, math notions whose foundations have been matters of continuous debate have often yielded the most mileage; the notion of an infinitesimal is perhaps the best-known example. Unlike the infinitesimal, number is not the exclusive property, or even, largely, the personal property, of the mathematician. Number has been a concept of social importance since the dawn of recorded history. The significance to society of number and number-related skills has increased tremendously with the rise of industrial civilization. Real Numbers Every measurement of quantities implies a vague notion of real numbers. From (the math point of view, the origins of the theory of real numbers can be traced back to the progressive formation by the Babylonians of a system of numeration which was (in principle) capable of representing arbitrarily close approximations to any real number. The possession of such a system, and the confidence in numerical calculation which naturally resulted from it, inevitably led to a "naive" notion of real number which differs hardly at all from that which is current today (linked with the decimal system of numeration) in elementary education and among physicists and engineers. This notion cannot be precisely defined, but can be expressed by saying that a number is regarded as defined by the possibility of finding approximations to it and using these approximations in calculation; this necessarily implies a certain amount of confusion between measures of physical quantities, which, of course, are not susceptible to an infinite series of successively closer and closer approximation, and "numbers" such as A similar "pragmatic" attitude appears in all math schools in which experience in calculation is more important than rigour and theory. The latter, however, were predominant in Greek maths and it is to the Greeks that we owe the first rigorous and coherent theory of ratios of magnitudes, that is, essentially, of real numbers. This theory was the culmination of a series of discoveries about proportions and, in particular, incommensurable ratios, whose importance in the history of Greek thought can hardly be exaggerated, but which in the absence of accurate texts can be discerned only in outline. Greek maths in its early stages was inextricably bounded up with speculations, part scientific and part philosophical and mystical, about proportion, similitude and ratios, especially "simple ratios" (expressible by fractions with small numerators and denominators) and one of the characteristic tendencies of the Pythagorean school was to attempt to explain all in terms of integers and ratios of integers. But it was the Pythagorean school, in fact, which discovered that We know little about the movement of ideas which accompanied and followed) this important discovery. We shall give only a brief summary of the main ideas 'which lie at the base of the theory' of ratios of magnitudes which was constructed by the great mathematician Eudoxus (a contemporary and friend of Plato), definitely adopted by classical Greek maths and is known to us through Euclid's Elements. 1) The word and the idea of number are strictly reserved to natural integers In this the Greek mathematicians separated themselves voluntarily from the "logisticians" or professional calculators who, like their Egyptian and Babylonian predecessors, had no scruples about treating fractions as if they were numbers, or adding a fraction to an integer. It seems moreover that this self-imposed restriction on the concept of number came from philosophical rather than math motives and followed the reflections of the first Greek thinkers on the unit and the multiple, the unit (in this system of thought) being incapable of subdivision without thereby losing its character of unit. 2) The theory of magnitudes is based on axioms, which applied simultaneously to all types of magnitudes (there are allusions to earlier theories which apparently treated lengths, areas, volumes, times, etc., all separately). Magnitudes of the same type are characterized by the facts that they can be compared (that is to say, it is assumed that equality, which is an equivalence relation, and the relations For Eudoxus, the magnitudes of a given type form a system with one internal law of composition (addition), but that this system has an external law of composition whose operators are ratios of magnitudes, conceived of as forming an Abelian multiplicative group. The universal domain of operators thus constructed was the equivalent, for the Greek mathematicians, of what the set of real numbers is for us; moreover, it is clear that, with addition of magnitudes and multiplication of ratios of magnitudes they possessed the equivalent of what the field of real numbers is for us, although in a much less manageable form. Such was the state of the theory of real numbers in the classical period of Greek maths. Admirable though Eudoxus' construction was, and leaving nothing to the desired in rigour or coherence, nevertheless, it must be admitted that it lacked flexibility and did not encourage the development of numerical calculation, still less the development of algebraic calculation. Moreover, its logical necessity could not be apparent except to those in love with rigour and familiar with abstraction; thus, it is natural that, with the decline of Greek maths, the "naive" point of view, which had been preserved through the tradition of the logisticians, should gradually re-emerge. This point of view is dominant, for example, in Diophantus who in truth was an upholder of this tradition rather than of official Greek science. He reproduces the Euclidean definition of number, but in reality he used the word "number" to mean the unknown in algebraic problems whose solution may be either an integer, or a fraction, or an irrational number. Although this change of attitude on the subject of number is connected with the development of algebra, it does not, of course, constitute an advance in itself, but rather a retreat. We cannot trace the vicissitudes of the concept of number through Hindu, Arab, and western maths up to the end of the Middle Ages. The "naive" notion of number predominated, and although Euclid's Elements served as a basis for the teaching of maths during this period, it is most likely that the doctrine of Eudoxus remained generally uncomprehended because the need for it was no longer appreciated. The "ratios" of Euclid were customarily described as "numbers", and the rules for calculating with integers were applied to them without any attempt to analyse the reasons for the success of these methods. Nevertheless, we see R. Bombelli, as early as the middle of the 16thcentury, expounding a point of view on this subject in his Algebra which is essentially correct; having realized that once the unit of length has been chosen, there is a one-to-one correspondence between lengths and ratios of magnitudes, he defines the various algebraic operations on lengths (assuming, of course, that the unit has been fixed) and, representing numbers by lengths, obtains the geometrical definition of the field of real numbers and thus gives his algebra a solid geometrical foundation. In the following two centuries the definitive establishment of correct methods was twice retarded by the development of two theories: the infinitesimal calculus and the theory of series. In the seventeenth century the main subject of debate was the notion of "infinitely" small, which though justified a posteriori by the results which were obtained with its help, seemed to be in open opposition to the axiom of Archimedes; and we see the most enlightened minds of this period finally adopting a point of view which differed little from that of Bombelli, and which is distinguished above all by the greater attention it paid to the rigorous methods of the ancients. Isaac Barrow (Newton's teacher, who himself played an important part in the creation of the infinitesimal calculus) recognized the need to return to the theory of Eudoxus in order to regain the proverbial "geometrical certainty" in the subject of number. On the other hand, defining numbers to be symbols which denote ratios of magnitudes and to be capable of being combined by the operations of arithmetic, Barrow obtains the field of real numbers in terms which Newton took up again in his Arithmetic and which his successors up to Dedekind and Cantor did not change. But it was in this period that the method of expansion in series was introduced; this rapidly took on an extremely formal character in the hands of impenitent algebraists and deflected the attention of mathematicians from the questions of convergence which are essential to any sound use of series in the domain of real numbers. At the same time began the movement of ideas which led to the definition of continuous functions and the general definition of compact spaces. Weierstrass had perceived the logical importance in making the idea of real numbers entirely independent of the theory of magnitudes; the latter is effectively equivalent to an axiomatic definition of the points of the line (and thus of the set of real numbers) and the assumption of the existence of such a set. Although this method is essentially correct, it is evidently preferable to start only from the rational numbers, and to construct the real numbers from them by completion. This was achieved, by diverse methods and independently of each other, by Weierstrass, Dedekind, Meray and Cantor; while the method of "cuts", proposed by Dedekind came very near to the definitions of Eudoxus. Simultaneously, Cantor began to develop the theory of sets of real numbers, the idea of which was first conceived by Dedekind, and thus obtained the principal elementary results on the topology of the real line, the structure of its open and closed sets, the notion of derived set and of totally disconnected perfect set. Cantor also obtained Theorem I on the power of the continuum and deduced from it that thecontinuum is uncountable, that the set of transcendental numbers has the power of the continuum, and also (a paradoxical result for its time) that the set of points of a plane (or of space) has the same power as the set of points of a line. With Cantor these questions assumed practically their definitive form. Apart from leading to work on general topology and applications to integration Cantor's work has led to investigations of the structure and classification of sets of points on a line, and a realvalued functions of a real variable. These have theirorigin in the work of Borel which was directed mainly towards measure theoryand "Borel sets".
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.220.239 (0.01 с.) |

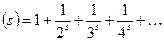
 .
. does not represent a rational number. He developed an ingenious theory of "equal ratios" which with just a few minor refinements could have become the basis for the real number system. Probably, Eudoxus was not understood by more than a very few contemporaries; it is doubtful whether any of them (and this may well include Euclid himself) could have foreseen the tremendous implications of this discovery.
does not represent a rational number. He developed an ingenious theory of "equal ratios" which with just a few minor refinements could have become the basis for the real number system. Probably, Eudoxus was not understood by more than a very few contemporaries; it is doubtful whether any of them (and this may well include Euclid himself) could have foreseen the tremendous implications of this discovery. was to be regarded as a "superordinate class" whose members, "subordinate classes", each contain precisely n elements. Given two subordinate classes, A and B, the two are said to be members of the same superordinate class, that is, instances of the same number, if and only if a one-to-one correspondence can be established between their respective elements. If instead the correspondence is many to one, then A and В are said to be instances of different numbers.
was to be regarded as a "superordinate class" whose members, "subordinate classes", each contain precisely n elements. Given two subordinate classes, A and B, the two are said to be members of the same superordinate class, that is, instances of the same number, if and only if a one-to-one correspondence can be established between their respective elements. If instead the correspondence is many to one, then A and В are said to be instances of different numbers. ,
, 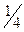 and so on) satisfy the axioms, as will any series of math or empirical entities that has a beginning, no repetitions and no end and is such that every entity can be reached in a finite number of steps. In short,, the domain of application of the ordinal theory is much wider than the series of natural numbers.
and so on) satisfy the axioms, as will any series of math or empirical entities that has a beginning, no repetitions and no end and is such that every entity can be reached in a finite number of steps. In short,, the domain of application of the ordinal theory is much wider than the series of natural numbers. (1 is the monad and not, strictly speaking, a number), to the exclusion not only of our irrational numbers but also of what we call rational numbers: to the Greek mathematicians of the classical period the latter are ratios of numbers. There is much more here than a simple question of terminology: the word "number" was for the Greeks (and for the moderns up to a recent time) linked with the idea of a system with two laws of composition (addition and multiplication); ratios of integers were regarded by the classical Greek mathematicians as operators, defined on the set of integers or on some subset of this set [the ratio of
(1 is the monad and not, strictly speaking, a number), to the exclusion not only of our irrational numbers but also of what we call rational numbers: to the Greek mathematicians of the classical period the latter are ratios of numbers. There is much more here than a simple question of terminology: the word "number" was for the Greeks (and for the moderns up to a recent time) linked with the idea of a system with two laws of composition (addition and multiplication); ratios of integers were regarded by the classical Greek mathematicians as operators, defined on the set of integers or on some subset of this set [the ratio of  to
to  is the operator, which, applied to
is the operator, which, applied to  , if
, if  forming a multiplicative group but not a system with two laws of composition].
forming a multiplicative group but not a system with two laws of composition]. and
and  are defined), that they can be added and subtracted (
are defined), that they can be added and subtracted ( is defined, and also is
is defined, and also is  if
if  ) and that they satisfy "Archimedes' axiom". It is clearly realized from the beginning that this latter fact is the key stone of the whole edifice (it is, in fact, indispensable in any axiomatic characterization of real numbers).
) and that they satisfy "Archimedes' axiom". It is clearly realized from the beginning that this latter fact is the key stone of the whole edifice (it is, in fact, indispensable in any axiomatic characterization of real numbers).


