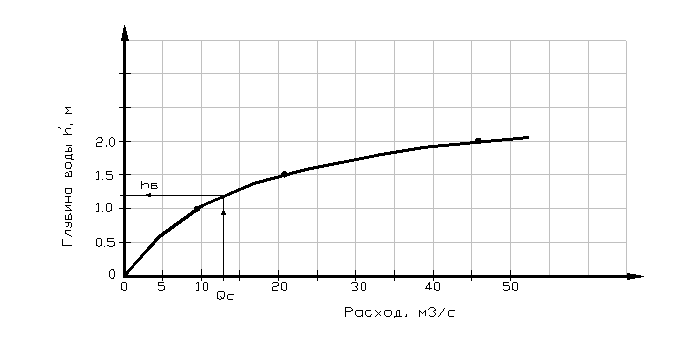Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение расчетного расхода ливневых водСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Расчетный расход ливневых вод рекомендуется определять по формуле:
где ap – расчетный коэффициент склонового стока, определяется по формуле (2.2.5); F – площадь водосбора, км2; j – коэффициент редукции стока в зависимости от пощади водосбора, определяется по формуле (2.2.8); Кi – коэффициент, учитывающий влияние крутизны склонов на расчетный расход, определяется по формуле (2.2.9); Кф – коэффициент, учитывающий форму водосбора, определяется по формуле: Расчетная интенсивность осадков вычисляется по формуле:
где
Кt – коэффициент редукции часовой интенсивности ливня, зависящий от площади водосбора F. При площади водосбора F=10км2 и менее принимается Кt=1,0, при площади водосбора F более 10км2 коэффициент Кt определяется по формуле:
Расчетный коэффициент склонового стока:
где
где
Коэффициент редукции максимального стока:
Коэффициент, учитывающий крутизну склонов:
где
Пример 2.2 Исходные данные. Трасса дороги II технической категории пересекает малый водоток с площадью водосбора F=3,62 км2 , длиной главного лога L=2,64 км. Общий уклон лога J=5,54‰. Грунты водосбора – суглинки. Необходимо определить максимальный расход воды, притекающий к трубе в период ливня. Решение. Примем вероятность превышения паводка 2% для дороги II технической категории. По формуле (2.2.1) находим:
Составляющие формулы (2.2.1) вычислены по (2.2.2) – (2.2.9) где
Построение графика зависимости расхода воды от глубины
График зависимости расхода от глубины воды Q=f(h) необходим для определения бытовой глубины hб во время расчетного паводка в нестесненном живом сечении водотока после пересечения его дорогой. В качестве расчетного расхода принимают сбросной расход, на который проектируется водопропускное сооружение. Для построения графика зависимости расхода воды от глубины Q=f(h) задаются несколькими уровнями воды Н и для каждого из них вычисляют глубину потока h на вертикалях, скорости потока на вертикалях, элементарные расходы. Скорость на вертикалях при глубине воды hi вычисляют по формуле:
где m – коэффициент, учитывающий шероховатость лога и склонов; Jс – уклон лога у сооружения в долях единицы.
Коэффициент m назначается для ровного земляного русла – 25, извилистого или заросшего русла (ручей) – 20, сильно заросшего – 10 – 15. Элементарный расход на вертикалях рассчитывается по формуле:
Расход в элементе живого сечения при расстоянии между вертикалями Li рассчитывается по формуле:
где
По данным об элементарных расходах строят их эпюру по ширине живого сечения потока. Суммарный расход при данном уровне равен площади эпюры элементарных расходов. Расчет производят в табличной форме (табл. 2.3.1) Таблица 2.3.1
Пример 2.3
Исходные данные. Уклон водотока у сооружения 10%o, русло сильно заросшее (m=15).
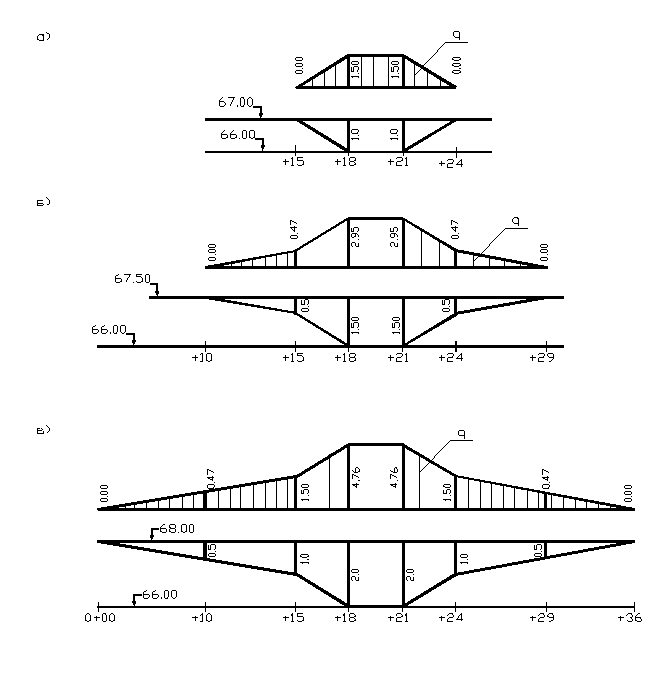
Поперечное сечение водотока характеризуется черными отметками, приведенными в метрах:
Таблица 2.3.2
Требуется построить график зависимости Q=f(h).
Задаем уровень воды 67,00, вычисляем глубины (рис.2.3.1а) на вертикалях, соответствующих точкам 0+18, 0+21, и вычисляем скорости движения воды по формуле (2.3.1), элементарные расходы по формуле (2.3.2). Эти данные заносим в таблицу 2.3.2 и строим эпюру элементарных расходов (рис.2.3.1а). Эта эпюра состоит из двух треугольников и прямоугольника. Вычисляем их площадь и заносим в таблицу 2.3.2 (графа 7). Суммарная площадь эпюры равна расходу при уровне 67,00. Принимаем отметки уровня 67,50 и 68,00 и проводим аналогичные вычисления. Строим эпюры элементарных расходов (рис.2.3.1б, 2.3.1в), вычисляем их площади (табл. 2.3.2), равные расходами при уровнях 67,50 и 68,00. Уровням 67,00; 67,50 и 68,00 (рис.2.3.1) соответствуют максимальные глубины 1,0; 1,50; и 2,0 м и расходы (табл. 2.3.2) 9,0; 21,47 и 47,66 м3/с. По полученным данным строим график зависимости расхода воды от глубины Q= f (h) (рис 2.3.1).
Таблица 2.3.2
Рис. 2.3.2 График зависимости Q= f (h) по данным примера
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.35.234 (0.009 с.) |

 , м3/с (2.2.1)
, м3/с (2.2.1)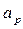 – расчетная интенсивность осадков мм/мин, определяется по формуле (2.2.2);
– расчетная интенсивность осадков мм/мин, определяется по формуле (2.2.2);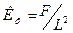 , где L – длина водосбора
, где L – длина водосбора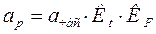 , мм/мин (2.2.2)
, мм/мин (2.2.2) – максимальная часовая интенсивность ливня, определяемая по формуле для заданной вероятности превышения ВП в процентах;
– максимальная часовая интенсивность ливня, определяемая по формуле для заданной вероятности превышения ВП в процентах; , мм/мин (2.2.3)
, мм/мин (2.2.3)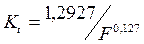 , (2.2.4)
, (2.2.4) , (2.2.5)
, (2.2.5) – коэффициент склонового стока при полном насыщении почв водой, определяется по формуле:
– коэффициент склонового стока при полном насыщении почв водой, определяется по формуле: , (2.2.6)
, (2.2.6) – коэффициент, учитывающий естественную аккумуляцию стока на поверхности водосбора в зависимости от залесенности и почво-грунтов, определяемый при сплошной залесенности при однородных грунтах по всему водосбору по формуле:
– коэффициент, учитывающий естественную аккумуляцию стока на поверхности водосбора в зависимости от залесенности и почво-грунтов, определяемый при сплошной залесенности при однородных грунтах по всему водосбору по формуле: , (2.2.7)
, (2.2.7) – коэффициент, учитывающий различную проницаемость почво-грунтов на склонах водосбора (принимается равным 0,04 – 0,09 при суглинках, 0,05 – 0,09 при супесях, песках, задернованных почвах и 0,15 – 0,20 в лесу);
– коэффициент, учитывающий различную проницаемость почво-грунтов на склонах водосбора (принимается равным 0,04 – 0,09 при суглинках, 0,05 – 0,09 при супесях, песках, задернованных почвах и 0,15 – 0,20 в лесу); – коэффициент, учитывающий состояние почво-грунтов к началу формирования расчетного паводка, принимается равным 1,05 – 1,10 для суглинков и 1,10 – 1,15 для супесей и песков.
– коэффициент, учитывающий состояние почво-грунтов к началу формирования расчетного паводка, принимается равным 1,05 – 1,10 для суглинков и 1,10 – 1,15 для супесей и песков. , (2.2.8)
, (2.2.8) , (2.2.9)
, (2.2.9)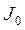 – общий уклон водосбора, ‰.
– общий уклон водосбора, ‰.
 ,
, ,
, ,
, ,
,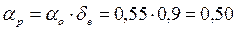 ,
, ,
, ,
,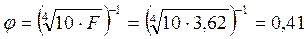 ,
, ,
,
 , (2.3.1)
, (2.3.1)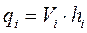 , (2.3.2)
, (2.3.2)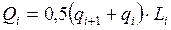 , (2.3.3)
, (2.3.3) – элементарные расходы на соседних вертикалях.
– элементарные расходы на соседних вертикалях.