
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямоугольная система координат и радиус-вектор.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если в пространстве выбрана прямоугольная система координат, (рис. 1.4), то координатами точки называются координаты радиус-вектора этой точки.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Задача 1.1. Построить вектор Решение. Из одного начала строим векторы
А Рис. 1.5 Рис. 1.6 Задача 1.2. Векторы
или АВС имеем
Так как модуль вектора есть величина неотрицательная, то Ответ. Задача 1.3. Векторы
началу и строим параллелограмм ABCD (рис. 1.8). По условию задачи тогда Вспомним, что углом между векторами
или
Аналогично из или
Ответ:
Задача 1.4. В параллелепипеде
Решение. 1) Для построения вектора по правилу многоугольника рассмотрим ломаную из векторов 2) Вектор
Рис. 1.9 Рис. 1.10 3) Для определения Ответ. 1)
Задача 1.5. Найти единичный вектор, коллинеарный данному вектору Решение. Искомый вектор Ответ.
параллелограмма ABCD. Выразить через векторы диагоналей (рис. 1.11) параллелограмма. Рис. 1.11 Решение. По правилу сложения
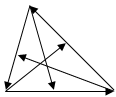
Задача 1.7. В треугольнике ABC проведены медианы AD, BE, CF. Доказать равенство
Задача 1.8. Найти зависимость между векторами Решение. Так как Ответ.
Задача 1.9. Векторы Решение.
Задача 1.10. Векторы Решение. Из
Задача 1.11. Даны три некомпланарных вектора Решение. По условию задачи следует доказать, что существует линейная комбинация векторов
Так как по условию задачи векторы
Откуда имеем Задача 1.12. В ромбе ABCD Решение.
Задача 1.13. В треугольной пирамиде ABCD Решение. Ответ.
Задача 1.14. В задаче 1.13 точка Q (рис. 1.14) – точка пересечения медиан грани BCD. Найти координаты вектора Решение. Для определения координат вектора
Следовательно, координаты
Задача 1.15. Известно разложение векторов
Решение. Имеем Ответ.
Задача 1.16. Проверить коллинеарность векторов Решение. Так как координаты векторов пропорциональны, то Задача 1.17. В треугольнике с вершинами в точках
так как
то
Ответ. Все формулы, необходимые для самостоятельного решения задач, приведены в таблице 1, в конце главы.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. По данным векторам 1) 2. Векторы Ответ. 3. Какому условию должны удовлетворять векторы 1) Ответ. 1) Векторы взаимно перпендикулярны. 2) Угол между векторами должен быть острым. 3) Угол между векторами должен быть тупым. 4. Какому условию должны удовлетворять векторы Ответ. 5. По данным векторам 1) 3 6. В параллелепипеде 1) 7. Даны два вектора 1) Ответ. 1) 8. Определить при каких a, b векторы Ответ. a =4, b =–1. 9. Принимая в качестве базиса векторы Ответ: 10. Даны точки А (3,–1,2) и В (–1,2,1). Найти координаты векторов Ответ. 11. Проверить коллинеарность векторов Ответ. 12. Разложить вектор Ответ. 13. Доказать, что для любых заданных векторов 14. В тетраэдре OABC медиана AL грани ABC делится точкой М в отношении Ответ. 15. В тетраэдре ABCD, DM – медиана грани BCD и Q – центр масс этой грани. Найти координаты векторов Ответ. 16. Заданы векторы Ответ. 17. Показать, что тройка векторов Ответ. 18. Дан вектор Ответ.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.208.109 (0.012 с.) |

 z
M
z
M
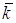 0
0  y
y
 x Рис. 1.4
x Рис. 1.4
 имеет координаты x, y, z, то координатами точки М будут числа x, y, z, что записывается в виде М (x,y,z).
Если даны две точки
имеет координаты x, y, z, то координатами точки М будут числа x, y, z, что записывается в виде М (x,y,z).
Если даны две точки  , то
, то  и
и 
 , если известны векторы
, если известны векторы  и
и  .
. (рис. 1.5) и
(рис. 1.5) и 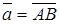 . Далее строим параллелограмм со стороной АВ и диагональю АС (рис. 1.6). Тогда по правилу параллелограмма
. Далее строим параллелограмм со стороной АВ и диагональю АС (рис. 1.6). Тогда по правилу параллелограмма 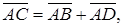
 .
. С D C
С D C
 В A B
В A B Определить
Определить  и
и 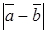 .
.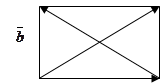 Решение. Так как
Решение. Так как  , то параллелограмм, построенный на этих векторах, будет прямоугольником ABCD (рис. 1.7) и
, то параллелограмм, построенный на этих векторах, будет прямоугольником ABCD (рис. 1.7) и 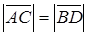 D C
D C . Из прямоугольного треугольника
. Из прямоугольного треугольника или А
или А  Рис. 1.7
Рис. 1.7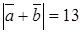 .
. .
. , причем
, причем  . Определить
. Определить  Решение. Векторы
Решение. Векторы  ; АВ
; АВ . Рис. 1.8
. Рис. 1.8 . По правилу параллелограмма
. По правилу параллелограмма  . Из
. Из 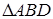 имеем
имеем
 .
.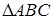 имеем
имеем 
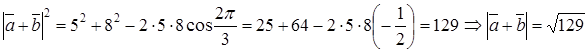

 (рис. 1.9) заданы векторы, совпадающие с его ребрами:
(рис. 1.9) заданы векторы, совпадающие с его ребрами:  Построить векторы
Построить векторы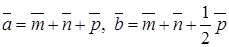 и
и  .
. :
:  , где
, где  . Вектор
. Вектор  замыкающий построенную ломаную
замыкающий построенную ломаную 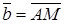 будет замыкающим для ломанной ABCM (рис. 1.10), где
будет замыкающим для ломанной ABCM (рис. 1.10), где 

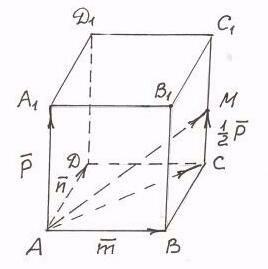
 вначале строим
вначале строим 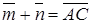 (по правилу параллелограмма), затем находим разность
(по правилу параллелограмма), затем находим разность  следовательно,
следовательно, 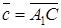 .
. , 2)
, 2)  , 3)
, 3)  .
.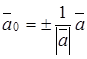 , так как
, так как  . Следовательно, имеем два решения.
. Следовательно, имеем два решения.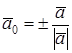 .
. Задача 1.6. Векторы
Задача 1.6. Векторы  и
и  служат сторонами D C
служат сторонами D C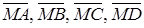 , где М – точка пересечения А
, где М – точка пересечения А  В
В ,
,  используя определение произведения вектора на число, имеем
используя определение произведения вектора на число, имеем 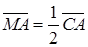 , но
, но  . Следовательно,
. Следовательно,  . Аналогично
. Аналогично
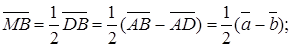

 (Вспомним, что нуль-вектор – это вектор, модуль которого равен нулю, а направление не определено).
(Вспомним, что нуль-вектор – это вектор, модуль которого равен нулю, а направление не определено). (рис. 1.12). Очевидно, что
(рис. 1.12). Очевидно, что  . Векторы
. Векторы  выразим через
выразим через  ,
,  ,
,  , откуда
, откуда
 С
D
Е
А F B
Рис. 1.12
С
D
Е
А F B
Рис. 1.12


 , то существует число
, то существует число  такое, что
такое, что 

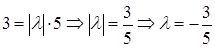 . Следовательно,
. Следовательно, 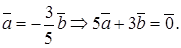
 .
. . Показать, что они коллинеарны.
. Показать, что они коллинеарны. .
. линейно зависимы с коэффициентами 4, 6, –2, т.е.
линейно зависимы с коэффициентами 4, 6, –2, т.е. 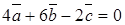 . Показать, что они компланарны.
. Показать, что они компланарны. . Следовательно,
. Следовательно, 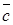 совпадает с диагональю параллелограмма, построенного на векторах
совпадает с диагональю параллелограмма, построенного на векторах  и
и 
 параллельны одной плоскости, а т.к.
параллельны одной плоскости, а т.к.  то
то  ,
,  компланарны.
компланарны. такая, что
такая, что 
 и
и  . Рассмотрим
. Рассмотрим  . Используя свойства сложения векторов и умножения вектора на число, последнее равенство запишем в виде:
. Используя свойства сложения векторов и умножения вектора на число, последнее равенство запишем в виде: .
.
 , где
, где  – произвольная постоянная, отличная от нуля. Таким образом, получим
– произвольная постоянная, отличная от нуля. Таким образом, получим  , где
, где 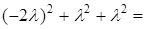
 .
. ,
,  (рис. 1.13). Разложить по векторам
(рис. 1.13). Разложить по векторам  и
и  .
. .
. A K C
B
Рис. 1.13
A K C
B
Рис. 1.13
 D
Q
D
Q
 C
A
M
B
Рис. 1.14
C
A
M
B
Рис. 1.14
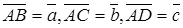 (рис. 1.14), DM – медиана грани DBC. Найти разложение вектора
(рис. 1.14), DM – медиана грани DBC. Найти разложение вектора  по векторам
по векторам 
 где
где 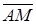 – половина диагонали параллелограмма, построенного на векторах
– половина диагонали параллелограмма, построенного на векторах  . Следовательно,
. Следовательно,  . Таким образом,
. Таким образом, 

 в базисе
в базисе 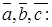

 . Символически это записывается так:
. Символически это записывается так: 


 . Найти в данном базисе координаты вектора
. Найти в данном базисе координаты вектора 
 откуда
откуда 
 и
и  Искомый вектор
Искомый вектор  =
= 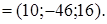

 и
и 
 . Из сравнения координат
. Из сравнения координат  следовательно,
следовательно, 
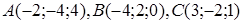 определить расстояние от вершины С до точки пересечения медиан треугольника (точка М на рис. 1.15).
определить расстояние от вершины С до точки пересечения медиан треугольника (точка М на рис. 1.15). А
N
M
B
C
Рис. 1.15
А
N
M
B
C
Рис. 1.15
 Следовательно, искомое расстояние равно модулю вектора:
Следовательно, искомое расстояние равно модулю вектора:

 ,
,



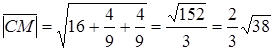 .
.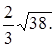
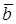 построить каждый из следующих векторов:
построить каждый из следующих векторов: +
+  , причём
, причём  и
и  . Определить
. Определить  и
и  .
. .
. , 2)
, 2)  , 3)
, 3)  .
. .
. ; 3)
; 3)  ; 4)
; 4)  .
.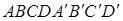 заданы векторы, совпадающие с его рёбрами
заданы векторы, совпадающие с его рёбрами  Построить каждый из следующих векторов:
Построить каждый из следующих векторов: , 2)
, 2)  .
. и
и  . Определить проекции на координатные оси следующих векторов:
. Определить проекции на координатные оси следующих векторов: ; 5) 2
; 5) 2  .
. 2)
2)  3)
3)  4)
4) 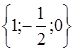 5)
5) 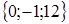 6)
6)  .
. и
и  коллинеарны.
коллинеарны. и
и  , совпадающие со сторонами треугольника ABC, определить разложение векторов, приложенных вершинах треугольника и совпадающих с его медианами.
, совпадающие со сторонами треугольника ABC, определить разложение векторов, приложенных вершинах треугольника и совпадающих с его медианами. ,
,  , где M,N,P – середины сторон треугольника АВС.
, где M,N,P – середины сторон треугольника АВС. и
и  .
.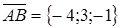 ,
,  .
. и
и  . Установить, какой из них длиннее и во сколько раз, как они направлены: в одну или в противоположные стороны.
. Установить, какой из них длиннее и во сколько раз, как они направлены: в одну или в противоположные стороны. по трём некомпланарным векторам:
по трём некомпланарным векторам:  .
. .
. векторы
векторы  ,
,  ,
,  компланарны.
компланарны. . Найти координаты вектора
. Найти координаты вектора  в базисе из рёбер
в базисе из рёбер  .
.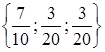 .
.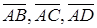 .
. ,
,  .
. и
и  . Разложить вектор
. Разложить вектор  по базису векторов
по базису векторов  .
. .
. ,
,  ,
, 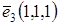 образует базис в множестве всех векторов пространства. Найти координаты вектора
образует базис в множестве всех векторов пространства. Найти координаты вектора  в базисе
в базисе  .
. .
. . Найти
. Найти  , если
, если  ,
,  ,
,  .
. или
или  .
.


