
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторов
Основные теоретические сведения Определение. Скалярным произведением векторов Скалярное произведение обозначается Из определения следует, что Свойства скалярного произведения. 1. 2. 3. 4. Скалярное произведение 5. 6. Если векторы заданы своими координатами в ортонормированном базисе Косинус угла между векторами: Если вектор ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Задача 2.1. a) Решение. Используя свойства скалярного произведения, находим: a) б) = =27 –4 –64 = –61; в) = Замечание. Квадрат суммы двух векторов раскрывается по формуле, используемой в обычной алгебре. Ответ. a) 9; б) –61; в) 13.
Задача 2.2. Решение. Из условия ортогональности двух векторов следует, что ( –
Ответ. Задача 2.3. Даны единичные векторы Решение. Способ 1. Векторы
Способ 2. (
Ответ. Задача 2.4. Даны векторы Вычислить: а) б) (2 в) ( г) Решение. Векторы a) б) Способ 1.
Способ 2. 2 Аналогично в) г) Координаты вектора
д) пр е) пр ж) Для решения этой задачи вспомним формулы для направляющих косинусов вектора
Замечание. {cos В нашем случае з) Пр = Ответ. а) 22; в) 41; д) б) – 200; г) 105; е)
Задача 2.5. Найти единичный вектор, имеющий противоположное вектору Решение. Орт вектора Ответ. Задача 2.6. Вектор Решение. Способ 1. Так как вектор Вектор Способ 2. Так как вектор Ответ.
Задача 2.7. Найти вектор Решение. Пусть
Решая систему, получаем Ответ.
Задача 2.8. Вычислить работу силы Решение. Найдем координаты вектора Ответ. 4 ед. работы.
Решение.
cos = Ответ. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Векторы
1) Ответ. 1) – 62, 2) 162, 3) 373. 2. Доказать справедливость тождества 3. Векторы Ответ. 4. Векторы Ответ. 5. Даны векторы Ответ. 1) 22, 2) 6, 3) 7, 4) –200, 5) 129, 6) 41. 6. Даны точки А (–1,3,–7), В (2,–1,5), С (0,1,–5). Вычислить 1) Ответ. 1) –524, 2) 13, 3) 3, 4) 7. Даны вершины четырёхугольника А (1,–2,2), В (1,4,0), С (–4,1,1), D (–5,–5,3). Доказать, что его диагонали АС и BD взаимно перпендикулярны. 8. Найти вектор Ответ. 9. Даны два вектора Ответ. 10. Найти проекцию вектора Ответ. –3. 11. Даны три вектора: Ответ. –11. 12. Вычислить длину диагоналей параллелограмма, построенного на векторах Ответ. 15, 13. Вычислить Ответ. 14. Найти длины сторон и величины углов треугольника с вершинами Ответ. 15. Для заданных векторов а) б) Ответ. а) 16. Найти косинус угла j между диагоналями АС и BD параллелограмма, если заданы три его вершины А (2,1,3), В (5,2,–1) и С (–3,3,–3). Ответ. 17. Даны векторы Ответ.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 752; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.193.45 (0.074 с.) |
 и
и  называется число
называется число 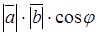 , где
, где  – длины векторов
– длины векторов  – угол межу этими векторами.
– угол межу этими векторами. или
или  .
.
 – коммутативность произведения.
– коммутативность произведения.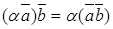 – ассоциативность относительно числового множителя.
– ассоциативность относительно числового множителя. – дистрибутивность суммы.
– дистрибутивность суммы. . Из определения скалярного произведения следует:
. Из определения скалярного произведения следует:  , т.е. скалярный квадрат вектора равен квадрату его модуля (длины).
, т.е. скалярный квадрат вектора равен квадрату его модуля (длины).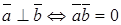
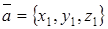 и
и 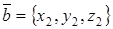 , то
, то  .
. .
. изображает силу, точка приложения которой перемещается из начала в конец вектора
изображает силу, точка приложения которой перемещается из начала в конец вектора  , то работа А этой силы вдоль указанного пути, определяется равенством
, то работа А этой силы вдоль указанного пути, определяется равенством  .
.
 ;
;  ;
;  =2p/3. Вычислить:
=2p/3. Вычислить: ; б)
; б) 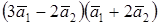 ; в)
; в)  .
.
 ;
;
 =
=  =
=  =
=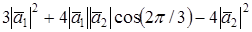 =3
=3  9+4
9+4  – 4
– 4 
 =
=  =9+2
=9+2  ;
;  . Определить, при каком значении
. Определить, при каком значении 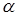 векторы
векторы  2 и
2 и 

 2=
2= 
 .
. и
и  , удовлетворяющие условию
, удовлетворяющие условию  +
+  . Вычислить
. Вычислить 

 образуют равносторонний треугольник, у которого стороны равны 1:
образуют равносторонний треугольник, у которого стороны равны 1:  ; (
; ( /3. (Почему? Рис.1.16).
/3. (Почему? Рис.1.16).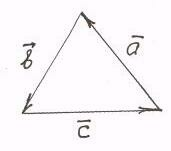 Рис. 1.16
Рис. 1.16


 cos(
cos(

 .
.


 2+
2+  2 +2(
2 +2(
 +
+  .
. ={4,–2,–4} и
={4,–2,–4} и  ={6,–3,2}.
={6,–3,2}. ; д) пр
; д) пр  ;
; –3
–3  ;
; ; з) пр
; з) пр  .
. = 4
= 4 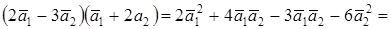

 .
. ={–10,5,–14}.
={–10,5,–14}. ;
;  =–10
=–10  =36–2
=36–2  ={2,–1,–10}, тогда
={2,–1,–10}, тогда =
=  =
=  .
. =
=  =
= 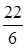 =
=  .
.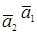 =
=  =
= 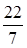 .
. { x,y,z }:
{ x,y,z }: 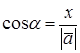 ,
,  ,
,  .
. , cos
, cos  }=
}=  – орт. вектора
– орт. вектора  .
. =
=  =6 и таким образом cos
=6 и таким образом cos 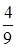 =
=  , cos
, cos  = –
= – 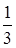 , cos
, cos 
 = –
= –  .
. ,
,  , так как
, так как  =
=  =7, то
=7, то  . Полученный вектор
. Полученный вектор  , поэтому искомым вектором является
, поэтому искомым вектором является 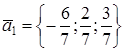 .
. , коллинеарный вектору
, коллинеарный вектору  =50, найти его координаты.
=50, найти его координаты.
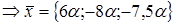 . Зная, что
. Зная, что 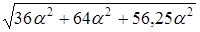 =50, откуда
=50, откуда  12,5
12,5  4.
4. . Вектор
. Вектор 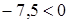 ), следовательно,
), следовательно, 
 = –
= –  = –4,
= –4,  ={1;–2;3} и удовлетворяет условию
={1;–2;3} и удовлетворяет условию 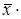 (2
(2  )= – 6.
)= – 6.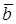 следует, что
следует, что  ,
,  . Известно также, что скалярное произведение вектора искомого вектора на данный:
. Известно также, что скалярное произведение вектора искомого вектора на данный:  . Таким образом, получаем систему трех линейных уравнений с тремя неизвестными x, y, z:
. Таким образом, получаем систему трех линейных уравнений с тремя неизвестными x, y, z:
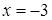 ,
, 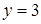 ,
,  , т.е.,
, т.е., 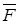 =
=  при перемещении материальной точки из положения А (–1,2,0) в положение В (2,1,3).
при перемещении материальной точки из положения А (–1,2,0) в положение В (2,1,3). , вдоль которого перемещается точка приложения силы:
, вдоль которого перемещается точка приложения силы:  (
( на пути
на пути 
 .
. Задача 2.9. Даны вершины треугольника А (3,2,–3), B (5,1,–1), C (1,–2,1). Определить его внешний угол при вершине А. B
Задача 2.9. Даны вершины треугольника А (3,2,–3), B (5,1,–1), C (1,–2,1). Определить его внешний угол при вершине А. B ^
^  ) (рис. 1.17).
) (рис. 1.17). =
=  = Рис. 1.17
= Рис. 1.17 =
=  ;
;  .
. .
. образует с ними углы, равные
образует с ними углы, равные  ; зная, что
; зная, что 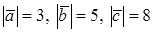 , вычислить:
, вычислить: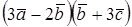 ; 2)
; 2)  ; 3)
; 3)  .
. и выяснить его геометрический смысл.
и выяснить его геометрический смысл.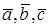 попарно образуют друг с другом углы, каждый из которых равен
попарно образуют друг с другом углы, каждый из которых равен  . Зная, что
. Зная, что 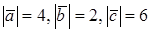 , определить модуль вектора
, определить модуль вектора  .
.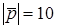 .
. образуют угол
образуют угол  ; зная, что
; зная, что  вычислить угол a между векторами
вычислить угол a между векторами  и
и  .
. .
. вычислить: 1)
вычислить: 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  , 5)
, 5) 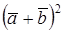 , 6)
, 6)  .
.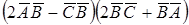 , 2)
, 2)  , 3)
, 3)  , 4) найти координаты вектора
, 4) найти координаты вектора  и
и  .
. и
и 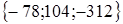 .
. и удовлетворяющий условию
и удовлетворяющий условию  .
. .
.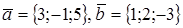 . Найти вектор
. Найти вектор  .
. .
. на ось, составляющую с координатными осями Ox, Oz углы
на ось, составляющую с координатными осями Ox, Oz углы  и
и 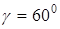 , а с осью Oy – острый угол b.
, а с осью Oy – острый угол b. Вычислить
Вычислить 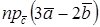 .
. , если известно, что
, если известно, что  и угол между ними
и угол между ними  .
. .
. , если
, если  и угол между ними
и угол между ними  .
.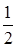 .
.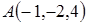 , В (–4,–2,0), С (3,–2,1).
, В (–4,–2,0), С (3,–2,1). ,
,  ,
,  ,
,  ,
,  .
. вычислить
вычислить 


 , б)
, б)  .
. .
. ,
,  и
и  . Найти
. Найти  ,
,  ,
, 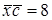 .
. .
.


