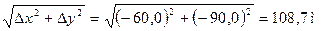Понятие о форме и размерах Земли

ЛЕКЦИЯ №1

ВВЕДЕНИЕ. ОБЩИЕ СВЕДЕНИЯ.

Геодезия (греч. «землеразделение») – наука об измерениях на земной поверхности, проводимых для определения формы и размеров Земли, изображении земной поверхности в виде планов, карт и профилей, а также для создания различных инженерных сооружений.

В процессе своего развития геодезия разделилась на ряд самостоятельных научных дисциплин – высшую геодезию, геодезию, инженерную геодезию, картографию, фототопографию и космическую геодезию.

Высшая геодезия занимается изучением вида и размеров Земли, а также определением геодезических координат отдельных точек земной поверхности.

Геодезия, часто называемая топографией, изучает методы съемки для изображения сравнительно небольших участков земной поверхности на планах или картах.

Инженерная геодезия призвана решать геодезические задачи, связанные с построением опорной геодезической основы для проведения съемочных и разбивочных работ, составлением крупномасштабных планов и профилей для проектирования инженерных сооружений; производством разбивочных работ в плане и по высоте при строительстве зданий и сооружений; текущим обслуживанием строительно-монтажных операций; составлением исполнительных чертежей возведенных объектов и исследованием их деформаций в процессе строительства и эксплуатации.

Космическая геодезия изучает геометрические соотношения между точками земной поверхности с помощью искусственных спутников Земли.

Геодезия имеет огромное значение в различных отраслях народного хозяйства. Особенно велика ее роль при картографировании страны.

Геодезические работы ведут при планировке, озеленении и благоустройстве населенных мест, при лесоустройстве и т.д. Комплексная механизация и автоматизация строительно-монтажных операций невозможна без высокой точности геодезических измерений.

При проектировании вертикальной планировки строительной площадки и подготовке выноса проектов зданий и сооружений в натуру составляют специальные разбивочные чертежи, на которых указывают линейные и угловые величины, определяющие положение на местности зданий и сооружений. Геодезические разбивочные работы обеспечивают соблюдение всех геометрических требований проекта и должны предусматриваться в технологических схемах возведения зданий и сооружений. В процессе возведения объектов выполняют контрольные геодезические измерения. После окончания строительства производят исполнительную съемку законченных объектов и составляют исполнительный генеральный план, используемый при эксплуатации зданий и сооружений. При эксплуатации сооружений ведут систематические геодезические наблюдения за их устойчивостью и прочностью.

 

 

Понятие о форме и размерах Земли

Физическая поверхность Земли, состоящая из суши и водной поверхности имеет сложную форму. Суша представляет сочетание низменностей и возвышений, высоты которых над уровнем моря достигают 8-9 км.

За математическую поверхность Земли принимают уровенную поверхность, которая представляет поверхность воды океанов в ее спокойном состоянии, мысленно продолженную под материки. В общем уровенная поверхность Земли не совпадает с поверхностью ни одной математической фигуры и представляет собой неправильную форму, которая называется геоидом.

 

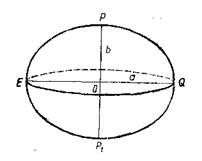
Рисунок 1.1 – Земной эллипсоид

В 1946г. под руководством профессора Ф.Н.Красовского вычислены размеры земного эллипсоида; большая полуось а=6378245 м, малая полуось b=6356863 м.

 

Рисунок 1.2 – Географическая система координат

Угол φ, называемый географической широтой, отсчитывается от плоскости экватора к северу и к югу от 0 до 90˚. Широты точек, расположенных в северном полушарии, называют северными, а в южном – южными.

Угол λ, называемый географической долготой, отсчитывается от плоскости начального меридиана к востоку и западу от 0 до 180˚. Точки, расположенные восточнее начального меридиана, имеют восточные долготы, а западнее – западные.

Зональная система прямоугольных координат Гаусса. Чтобы установить связь между географическими координатами любой точки на плоскости, применяют способ проектирования поверхности земного шара на плоскость по частям, которые называются зонами.

В такой системе начало координат для всех зон принимается в точке пересечения осевого меридиана данной зоны с экватором. Координатными осями являются соответственно ось абсцисс и ось ординат (рисунок 1.3)

 

Рисунок 1.3 – Зональная система координат

 

 

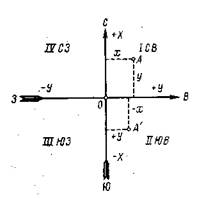
Абсциссы, отсчитываемые от экватора к северному полюсу, считаются положительными, на запад – отрицательными. Точка А₁ (рисунок 1.3) будет иметь координаты: абсциссу х_а и ординату у_а.

Система прямоугольных координат. В геодезической практике часто положение точек определяют плоскими прямоугольными координатами. В этой системе плоскость координат совпадает с плоскостью горизонта в данной точке О, являющейся началом этих координат; ось х всегда направлена на север, а ось у – на восток. Северное направление оси абсцисс считается положительным (+), южное – отрицательным (-); направление оси ординат считается положительным на восток и отрицательным на запад.

Оси координат делят плоскость чертежа на четыре части, которые называются четвертями: I – СВ, II – ЮВ, III – ЮЗ, IV – СЗ (рисунок 1.4)

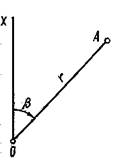
Рисунок 1.4 – Система прямоугольных координат.

Полярная система координат. В полярной системе координат (рисунок 1.5) положение любой точки А на плоскости определяется радусом-вектором r, исходящим из точки О, называемой полюсом, и углом β, отсчитываемым по ходу часовой стрелки от линии ОХ – полярной оси – до радиуса-вектора.

 

 

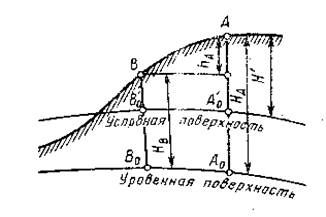
Рисунок 1.5 – Полярная система координат

Абсолютные и условные высоты. Спроектируем точку А (рисунок 1.6) физической поверхности Земли по направлению отвесной линии на уровенную поверхность. Высота Н_А этой точки, измеряемая от уровня моря, называется абсолютной, а Н', измеряемая от произвольной уровенной поверхности, - условной. Относительной высотой точки или превышением называется высота ее над другой точкой земной поверхности, она обозначается через h. Например, превышение точки А над точкой В составит h_А = Н_А – Н_{В .} Для определения высоты уровня моря на его берегу надежно закрепляют в вертикальном положении рейку с делениями – футшток и периодически фиксируют уровень моря относительно этой рейки.

 

 

Рисунок 1.6 – Абсолютные и условные отметки

 

В РФ высоты точек физической поверхности Земли отсчитываются от нуля Кронштадского футштока (черта на медной доске, установленной в гранитном устое моста через Обводной канал в Кронштадте).

Числовые значения высот точек называют отметками.

 

Контрольные вопросы

 

1. Что такое физическая и уровенная поверхность Земли?

2. Что называется географической широтой и долготой?

3. Какие системы координат применяются в геодезии?

4. Что называется абсолютной и условной высотой точки на земной поверхности?

5. Что называется относительной высотой точки на земной поверхности?

6. Что называется отметкой точки на земной поверхности?

 

ЛЕКЦИЯ №2

УРОК №2. МАСШТАБЫ ТОПОГРАФИЧЕСКИХ ПЛАНОВ И КАРТ. УСЛОВНЫЕ ЗНАКИ.

Понятие о геодезических планах и картах

Планом местности называется чертеж, представляющий собой уменьшенное и подобное изображение ее проекции на горизонтальную плоскость.

На плане длины линий, углы и площади контуров участков местности не искажаются, а степень уменьшения ее линейных элементов (масштаб изображения) постоянна для всех частей плана. Планы, на которых изображена только ситуация местности, называются ситуационными или контурными. Планы, на которых кроме предметов местности изображен еще и рельеф, называют топографическими.

Картой называется построенное по определенным математическим законам уменьшенное обобщенное изображение на плоскости всей Земли или значительных ее частей с учетом кривизны уровенной поверхности.

Карты в зависимости от масштабов условно делят на крупномасштабные – 1: 100000 и крупнее, среднемасштабные – от 1: 200000 до 1: 1000000, мелкомасштабные – мельче 1: 1000000.

При выполнении геодезических работ, входящих в комплекс строительно-монтажного производства, для составления планов применяют масштабы 1: 200, 1: 500, 1: 1000, 1: 2000, 1: 5000.

Профилем местности называется изображенное в уменьшенном виде сечение вертикальной плоскостью поверхности Земли по заданному направлению. Профили местности используют для строительства и монтажа надземных и подземных инженерных сооружений и сетей.

Топографические планы применяют в основном для строительного проектирования. На таком плане изображают весь комплекс подземных и надземных сооружений. В зависимости от размеров и назначения строительства его рабочий проект составляют в масштабе 1: 500 – 1: 1000, на отдельные объекты в зависимости от их сложности – в масштабе 1: 200 и крупнее.

 

Масштабы

Масштабом называется отношение длин линии на плане (профиле) к соответствующей проекции этой линии на местности. Следовательно, масштаб есть число отвлеченное – правильная дробь. Для удобства пользования и сравнения все масштабы имеют однообразный вид: числителем дроби всегда является единица; при этом знаменатель непосредственно выражает степень уменьшения

Численный масштаб – масштаб, где числитель выражен единицей.

S₀ / S = 1 / S:S₀ = 1/М (1)

 

В формуле (1) М – знаменатель численного масштаба, который показывает, во сколько раз были уменьшены проложения линий местности при изображении их на плане. Из численного масштаба следует, что определенной единице длины на плане соответствует 1000 или 2000 или 5000 и т.д. таких же единиц на местности. Например, 1см на разных планах или картах соответствует 1000, 2000, 50000, 10 000см на местности или в переводе на метры 10, 20, 50 и 100м.

При сравнении двух масштабов более крупным называют тот, у которого знаменатель меньше. Естественно, чем крупнее масштаб, тем больше подробностей может быть изображено на плане или карте. Планы, на которых должно быть показано больше подробностей, следует составлять в более крупном масштабе.

 

Линейный масштаб

Линейный масштаб строят следующим образом. На прямой АВ (рисунок 2.1)откладывают равные между собой отрезки, называемые основанием масштаба. Обычно длину принимают равной 1 или 2см.

 

 

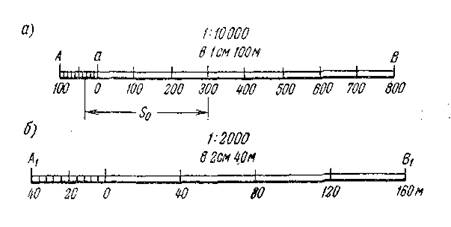
Рисунок 2.1 – Линейный масштаб

По заданному численному масштабу плана определяют число метров на местности, которому будет соответствовать принятое основание мас­штаба, Так, если за основание масштаба взят 1см, а численный масштаб равен 1: 10 000, то основание линейного масштаба будет соответствовать длине на местности 100м.

Первое основание А-а линейного масштаба (рисунок 2.1а)делят на десять равных частей. Правый крайний штрих а этого основания принимают за нуль — начало счета делений линейного масштаба. Вправо от нуля деления, равные основанию масштаба, выражают соответствующим чис­лом метров. При масштабе 1: 10 000 каждый сантиметр линейного мас­штаба, как уже было сказано, соответствует 100мна местности. Влево от 0 подписывают десятые доли основания, выраженные также в метрах. В рассматриваемом примере каждая десятая доля основания масштаба соответствует 10м.

Поскольку наименьшее расстояние, различимое глазом, равно 0,1мм, то, следовательно, пользуясь линейным масштабом, можно определять расстояния только в пределах до 0,1мм, что в приведенном на рисунке 2.1 примере соответствует одному метру на местности. Эта величина (0,1мм ) и является графической предельной точностью линейного масштаба. Для планов и карт, имеющих численный масштаб 1: 500,, 1: 1000, 1: 5000, 1: 10 000 и т. д., графическая предельная точность масштаба соответственно равна 0,05; 0,1; 0,5 и 1,0м.Это значит, что отрезки линий, меньше указанных, не могут быть выражены на плане или карте данного масштаба.

Линейным масштабом пользуются следующим образом. Если при помощи линейного масштаба, изображенного на рисунке 2.1а, нужно отло­жить на плане отрезок, соответствующий расстоянию 420м на местности, то правую ножку циркуля-измерителя совмещают с делением 400, рас­положенным правее нулевого деления, а левую совмещают со вторым делением основания масштаба, расположенным левее 0. Общий раствор циркуля-измерителя будет соответствовать заданному расстоянию на местности.

Если требуется узнать, какой длине на местности соответствует рас­стояние между двумя точками на плане, то для этого нужно циркулем-измерителем взять это расстояние S₀ на плане. Затем, не меняя раствора циркуля, правую его ножку совмещают с делением правой части линей­ного масштаба так, чтобы левая ножка циркуля разместилась несколько левее 0. Пусть правое деление будет 300и(см. рисунок 2.1а), а левая ножка циркуля расположилась левее нуля и заняла положение между третьим и четвертым делениями основания масштаба (А-а). Тогда расстояние на местности составит 300 + 30 = 330м,причем к этой величине надо еще добавить часть наименьшего деления между третьим и четвертым штри­хами. Эту часть определяют на глаз. Пусть она равна 0,4мм,что соответ­ствует 4м. Таким образом, расстояние S₀между точками на плане соот­ветствует 334мна местности.

Линейный масштаб можно построить и с основанием, равным 2см. На рисунке 2.1бизображен такой масштаб. При условии, если численный масштаб равен 1: 2000, основание линейного масштаба в данном случае будет соответствовать 40мна местности.

 

ПОПЕРЕЧНЫЙ МАСШТАБ

Для более точного построения плана или определения длин отрезков пользуются поперечным масштабом (рисунок 2.2).

 

 

 

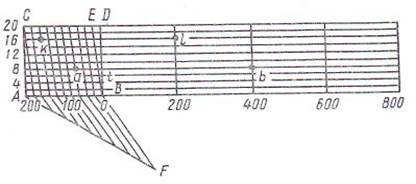
Рисунок 2.2 – Поперечный масштаб

За основание такого масштаба обычно принимаютотрезок АВ =2см и делят его на 10 равных частей. Для этого под произвольным углом к основа­нию проводят прямую AF и на ней от точки А откладывают 10 произвольных, но равных частей; соединив точки В и F, проводят через все точкилинии AF прямые, параллельные ВF, которые и разделят основание на 10 равных частей. Далее, на линии АС, перпендикулярной АВ откладывают 10 произвольных, но равных между собой отрезковичерез полученные точки проводят линии, параллельные АВ. Отрезки междунаклонными линиями, парал­лельными BE, равны десятым долям основания АВ, т. е. ED = АВ/10

Отрезки, заключенные между перпендикуляром BD и наклонной BE, равны сотым долям основания, т. е. t = ЕD/10 = АВ/10*10 = АВ/100. Такой масштаб называют еще нормальным попереч­ным масштабом.

Цифры, написанные внизу масштаба, изображенного на рисунке 2.2, соответствуют численному масштабу 1:10 000. Тогда основание АВ для такого масштаба соответствует на местности 200м, а наимень­шее деление будет t = 200/10*10 = 2м. Отрезки ab и kl для данного случая будут соответствовать 468 и 356м.

 

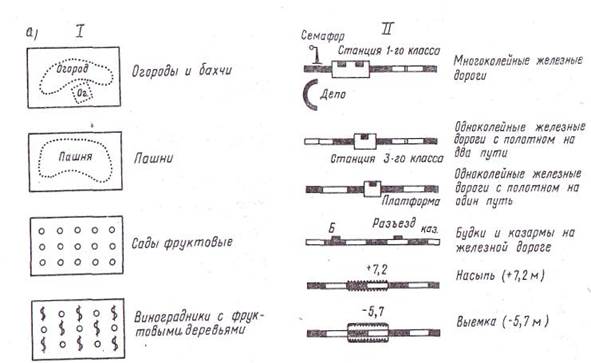
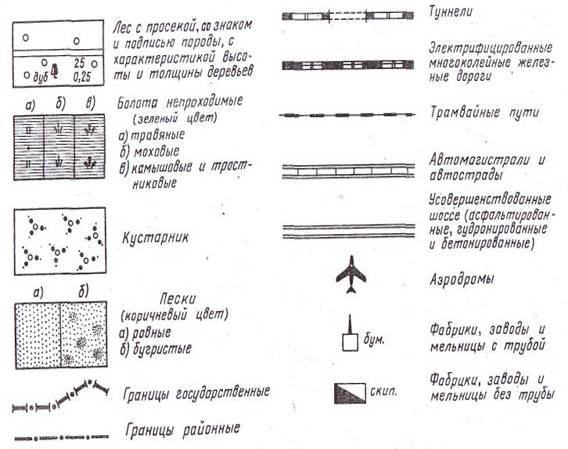
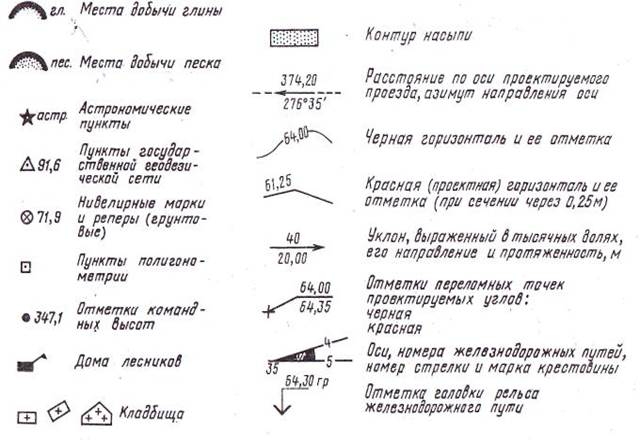
Условные знаки на планах, картах и геодезических чертежах

Для обозначения на планах и картах различных предметов местности применяют специально разработанные условные знаки. Для облегчения пользования планом или картой очертания условных знаков напоминают вид изображаемых элементов местности. Условные знаки для топографических планов и карт являются едины­ми для всей России. В основу создания условных знаков положено единство их начертания, поэтому для чтения планов и карт достаточно изучить условные знаки одного какого-нибудь масштаба.

Некоторую особенность представляют собой условные знаки разбивочных и исполнительных чертежей, которые применяются при проектировании генеральных планов сооружаемых объектов. Условные знаки принято делить на контурные, или масштабные, и внемасштабные.

Масштабными называют условные знаки, которыми предметы местности изображают с соблюдением масштаба карты или плана. Они дают возможность определить по плану или карте не только местоположение предмета, но и его размеры.

 

 

Контрольные вопросы

1.Что называется планом, картой, профилем местности?

2.Что называется масштабом?

3.Что представляют собой численный, линейный и поперечный масштабы?

4.Построить линейный масштаб, если численный равен: 1:500; 1:2000; 1:50 000.

5.Определить цену деления поперечного масштаба, если число делений на основании 10, а численный масштаб 1:500; 1:10000; 1:2500.

 

Приложение

 

 

 

 

 

 

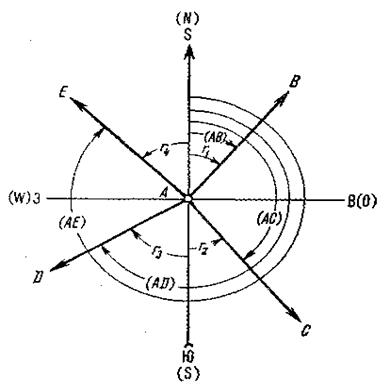
а - для топографических планов (I - масштабные, II - внемасштабные);

б - для геодези­ческих истроительных чертежей

Рисунок 2.3 – Условные знаки

ЛЕКЦИЯ № 3

ЛЕКЦИЯ №4

Ориентирование по румбам

Иногда для ориентирования линии местности пользуются не азимутами, а румбами.

Румбом называют угол( острый ), отсчитываемый от ближайшего (северного или южного) направления меридиана до линии, направление которой определяется.

Проведем через точку А меридиан С-Ю и линию В-З (восток-запад). Эти взаимно перпендикулярные линии с обозначением стран света буквами С, Ю, В и З образуют на плоскости четыре четверти, получившие нумерацию по ходу часовой стрелки и названия, составленные из соответствующих обозначений стран света. Так, первая четверть названа северо-восточной (СВ), вторая - юго-восточной (ЮВ), третья - юго-западной (ЮЗ), четвертая - северо-западной (СЗ).

 

 

 

Направление линии ОА определяется румбом r_ОА, который равен дирекционному углу этой линии

r_ОА = α_ОА

Направление линии ОВ определяется румбом r_ОВ

r_ОВ = 180º - α_ОВ

Направление линии ОС определяется румбом r_ОС

r_ОС = α_ОС - 180º

Направление линии ОД определяется румбом r_ОД

r_ОД = 360º - α_ОД

 

 

ЗАДАЧИ ДЛЯ ЗАКРЕПЛЕНИЯ

Пример 1. Азимут линии равен 112º. Определить румб этой линии.

 

Решение. Величина азимута указывает, что линия расположена во второй четверти, следовательно r₂ = 180º - 112º = 68º. r₂ = ЮВ:68º

 

 

Пример 2. Известен румб линии r = ЮЗ:56. Определить величину азимута, соответствующего этому румбу.

 

Решение. Так как румб имеет название ЮЗ, то линия расположена в третьей четверти и азимут ее будет равен А_ист = 180º + 56º = 236º

 

ЛЕКЦИЯ №5

Прямая геодезическая задача

В геодезии часто встречается задача, состоящая в том, что по прямоугольным координатам одной точки находят прямоугольные координаты другой точки, если известны расстояния между этими точками и дирекционный угол линии, их соединяющей.

Пусть (рисунок 5.2) даны прямоугольные координаты х_А и у_А точки А и полярные координаты s и α_АВ точки В

 

 

Рисунок 5.2

По этим данным надо найти прямоугольные координаты х_В и у_В точки В.

Из чертежа (рисунок 5.2) мы имеем:

х_В = х_А +∆ х

у_В = у_В +∆ у

Следовательно, чтобы найти координаты х_В и у_В , нужно к известным координатам х_А и у_А прибавить приращение ∆ х и ∆ у

Приращением называют разности ∆ х и ∆ у координат последующей и предыдущей точек.

Из прямоугольного треугольника (рисунок 5.2) АаВ имеем:

∆ х = s ∙ cos α_АВ

∆ у = s ∙ sin α_АВ

Так как линия может быть направлена под любым (0˚-360˚) углом α, то в расчете угол α заменяют румбом r, поэтому

∆ х = s ∙ cos r_АВ

∆ у = s ∙ sin r_АВ

В зависимости от направления линии АВ меняются знаки координат точек А и В, следовательно приращения координат тоже могут иметь разные знаки.

Таблица 5.1 – Зависимость знаков приращений от направления линий

Четверти	Приращения	Угол α (˚)	Румб r (˚)
∆ х	∆ у
I	+	+	0˚-90˚	0˚-90˚
II	-	+	90˚-180˚	180˚- α
III	-	-	180˚-270˚	α - 180˚
IV	+	-	270˚-360˚	360˚ - α

Поэтому формулы для определения прямоугольных координат последующей точки можно записать:

 

хВ = хА ± ∆ х уВ = уВ ± ∆ у

 

Примеры решения задач

Пример 1. Пусть даны х_А = 50,0м, у_А = 80,0м, s = 100м, α_АВ = 120˚30'. Необходимо вычислить координаты точки В: х_В и у_В.

Решение. Вычисления выполняют по следующей схеме. Так как дирекционный угол α_АВ больше 90˚, а именно 90˚-180˚, то данный отрезок находится во второй координационной четверти. В расчетах угол α_АВ заменяем на румб r. Для второй четверти румб будет равен

r_AB = 180˚- α_АВ = 180˚-120˚30' = 59˚30':ЮВ

r_AB = 59˚30':ЮВ

Так как отрезок АВ находится во второй четверти, знаки приращений будут

∆х (-); ∆у(+), поэтому формулы для вычисления координат точки В х_В и у_В.:

х_В = х_А - ∆х = х_А – s ∙ cos r_AB

y_В = y_А + ∆y = y_А – s ∙ sin r_AB

х_В = 50 – 100 ∙ cos 59˚30' = 50 – 100 ∙ 0,507538 = - 0,754

y_В = y_А + ∆y = y_А – s ∙ sin 59˚30' = 80 + 100 ∙ 0,861629 = 166,163

Правильность решения задачи можно подтвердить чертежом, выполнив его в масштабе.

 

Пример 2. Пусть даны прямоугольные координаты точек А и В. Необходимо найти дирекционный угол α_АВ и длину линии АВ – s.

х_А = 20,0м, у_А = 30,0м

х_В = - 40,0м, у_В = - 60,0м

Решение. Приращение координат вычислим по формуле:

∆ у = у_В – у_А = - 60 - 30 = -90,0

∆ х = х_В – х_А = - 40 – 20 = - 60,0

Так как знаки приращений отрицательные, то линия лежит в III четверти, где дирекционный угол будет равен:

r_AB = α_АВ - 180˚ => α_АВ = 180+ r_AB

Румб линии r_AB находим по формуле:

tg r_АВ =

По таблице находим значение угла для tg r_АВ =1,5 => r_АВ =56˚19', тогда

α_АВ = 180˚ + 56˚19' = 236˚19'

Длину отрезка АВ находим по формуле:

s_АВ =

 

Задачи для самоконтроля:

1. Определить координаты точки В: х_В и у_{В .}, если длина линии АВ

s_AB = 120м, координаты точки А х_А = - 10,5м, у_А = - 22,0м. дирекционный угол линии АВ α_АВ = 225˚35'.

 

2. Определить длину линии DС s_DC и ее дирекционный угол α_DC, если координаты начальной и конечной точек равны:

х_D = 22,5м, у_D = - 20,0м

х_C = 10,0м, у_C = 30,0м

свои решения подтвердить чертежами в масштабе 1:1000

 

 

ЛЕКЦИЯ №6

Единицы измерения

Измерение - есть процесс сравнения какой-либо величины с другой однородной с ней величиной, принятой за единицу измерения. Например, измерение длины отрезка прямой линии путем последовательного уклады­вания вдоль этой линии мерного прибора есть процесс сравнения двух однородных величин — измеряемой длины отрезка прямой линии с из­вестной длиной другого отрезка прямой, выраженной в единицах измере­ния.

В геодезии за единицу длины обычно принимают метр., Метр (в пере­воде сгреческого значит «мера») — одна из основных единиц Международ­ной системы единиц СИ (Международная система единиц СИ введена в действие с 1 января 1963г. ГОСТом 9867-61). С 1889 г. было принято следующее определение метра: единица длины — метр определяется расстоянием (при 0° С и нор­мальном относительном давлении) между осями двух средних штрихов, нанесенных на платино-иридиевом бруске, хранящемся в Международном бюро мер и весов и служащем прототипом метра, длина которого соответ­ствует одной десятимиллионной части Парижского меридиана (эллипсоид Деламбра).

По штрихам, нанесенным на этом прототипе, можно производить сли­чение других эталонов метра с точностью в пределах от одной до двух десятых микрона.. Однако для научных целей такая точность в наше время является недостаточной. Поэтому XI Генеральная конференция по мерам и весам (1960 г.) утвердила новый естественный и неуничтожаемый эталон метра, выраженный через длину световых волн, и установила новое опре­деление метра:

Метр - длина, равная 1650763,73 длин волн в вакууме излучения, соответствующего переходу между уровнями 2р₁₀ и 5d₅ атома крипто­на 86.

 

Международной системой единиц (СИ) установлена также единица плоского угла – радиан (рад). Радиан - угол между двумя радиусами круга, вырезающий на окружности дугу, длина которой равна радиусу. Для измерения плоских углов применяют другие, более мелкие едини­цы — градус, минуту, секунду. Один градус представляет собой 1/360 длины окружности, или

 

1 градус (^О) = 2πR/360 = πR/180

 

Поскольку длина радиуса R соответствует радиану (рад), можно написать:

1 градус (^О) = (π/180) рад = 1,75 * 10^-2 рад;

1 минута (') = (π/180*60) рад = 2,91 * 10^-4 рад;

1 секунда (") = (π/180*60*60) рад = 4,85 * 10^-6 рад;

1 радиан (рад)= 57° 17 ' 44 ",8 = 3437 ', 7 = 206 264 ",8.

Рисунок 6.1

длиной около 30 см и толщиной 4-6 см. Такие колья забивают в землю (рисунок 6.1, а) так, чтобы верхний торец кола был вровень с поверхностью почвы. Рядом с основным колом забивают второй (вспомогательный) – сторожок. Верхняя часть сторожка затесывается; она должна оставаться над поверхностью почвы. На затеске сторожка надписывают номер или другое обозначение закрепленной точки.

Для более точного обозначения точки в торец кола забивают гвоздь, который служит центром знака. Иногда для этой цели употребляют кованые гвозди, и центры знаков отмечают на шляпках этих гвоздей крестообразной насечкой или просверливанием углубления малого диаметра.

Для облегчения розыска пунктов на местности их окапывают канавкой в форме треугольника, квадрата или круга (рисунок 6.1).

В тех случаях, когда обозначаемая на местности точка должна быть закреплена на более длительное время, вместо кола в землю зарывают специально изготовленный деревянный столб. Нижняя его часть, зарываемая в землю, просмаливается или обжигается и к ней прибивается «якорь» (рисунок 6.1, б). для более точного обозначения центра знака в торец верхнего заостренного конца столбика забивают гвоздь.

Иногда пункты закрепляют в виде обрезков железных труб или металлических стержней (рельсов) с бетонным «якорем» (рисунок 6.1, в). Центр знаков, закрепленных металлическим стержнем, отмечается просверливанием в торце стержня небольшого углубления тонким сверлом.

При обозначении точек в городах в асфальтовые покрытия улиц и тротуаров вместо кольев забивают костыли или гвозди

Рисунок 6.2

 

Все же длины ВС и. АС также могут быть определены, но только косвенно по­средством других величин. Если непосредственно измерить длину АВ и углы α и β, то из решения треугольника АВС (способами, известными из тригонометрии) можно вычислить по известной стороне и двум прилегающим к ней углам длины сторон ВС и АС.

Таким образом, в геодезии различают непосредственные и косвенные способы измерения длин линий на местности.

Меры длины

Посвоему назначению меры длины подразделяют на три основные группы:

1. эталоны единицы измерения длины,

2. образцовые меры,

3. ра­бочие меры длины.

 

Эталоны единицы измерения длины служат основной мерой длины в стране. Эталоны изготавливают для постоянного хранения и вос­произведения принятой единицы длины.

В 1889 г. был изготовлен и утвержден 31 эталон метра. Эталон №. & принят в качестве международного. Остальные эталоны были распределены по жребию между странами, подписавшими Метрическую конвенцию. Россия получила два эталона метра с номерами 11 и 28. Последний (№ 28) в настоящее время является государственным эталоном длины и хранится во Всесоюзном научно-исследовательском институте метрологии им. Д. И. Менделеева.

Образцовые меры длины изготавливают очень тщательно, срав­нивают с эталоном, бережно хранят и употребляют только для сравнения с ними рабочих измерительных приборов.. Длина образцовой меры срав­нивается с эталоном при определенной температуре, которая указывается в паспорте образцовой меры.

Рабочие меры длины и рабочие измерительные приборы предназначаются для измерений на местности. Их действительная длина опреде­ляется из сравнения с образцовыми мерами.

Рисунок 6.3

пластинками, на которых обозначены числа метров. Полуметровые деле­ния отмечаются заклепками. Лента наматывается на специальное кольцо (рисунок 6.4). Для обозначения концов ленты при укладывании ее на местности служат стальные шпильки (рисунок 6.5). Комплект шпилек в количестве 10—11 штук надевается на проволочные кольца.

 

 

Рисунок 6.4

Рисунок 6.5

Шкаловые ленты обычно уже штри­ховых (6—10 мм), имеют несколько иное устрой­ство. Применяются они для более точных изме­рений. На концах таких лент наносятся шкалы с миллиметровыми делениями, как это показано на рисунке 6.3, б.

Концевые ленты (рисунок 6.3, в) отличаются от штриховых и шкаловых тем, что за длину таких лент принимают расстояние между концами ручек натянутой ленты. Концевые ленты удобны при измерении расстоя­ний между строениями, когда требуется начало мерного прибора прикла­дывать к стене здания. Концевые ленты дают меньшую точность, чем штри­ховые и шкаловые ленты, и поэтому их применяют при измерениях невы­сокой точности.

Для измерения небольших расстояний используют тесмяные и сталь­ные рулетки. Рулетками называют узкие тонкие ленты длиной 10—20м, заключенные в футляры. Более удобными, обеспечивающими несколько большую точность измерений, являются стальные рулетки. При измере­ниях высокой точности применяют мерные проволоки или свето- и радио­дальномеры.

Проволоки изготавливают из специального сплава. На концах мерных проволок прикрепляют шкалы.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Что называется измерением? Что значит измерить величину?

2.Какие единицы измерения существуют для измерения углов и длин?

3.Каким образом закрепляют линии на местности?

4.Когда используют прямые и косвенные способы измерения длин?

5.Когда возникают грубые ошибки измерений и можно ли их избежать?

6.Каким образом учитываются систематические ошибки?

7.Как избежать влияния случайных ошибок?

8.Назвать виды мерных приборов?

9.Что называется компарированием мерных приборов?

10.Назвать разновидности мер длины. Что такое эталон?

 

ИЗМЕРЕНИЕ ДЛИН ЛИНИЙ.

Рисунок 6.6

 

Второй способ менее точен, так как ближняя веха сразу закроет значительное пространство и помешает хорошо видеть остальные дальние вехи.

 

Рисунок 6.7

 

 

мерщик, подавая сигналы, устанавливает переднего мерщика в створе измеряемой линии. Передний мерщик, приподняв ленту, натягивает ее и укладывает по указанию заднего мерщика так, чтобы передний конец ленты оказался в створе измеряемой линии. Положение переднего штриха ленты отмечается шпилькой, которая вкалывается в землю в строго вертикальном положении точке 1 (рисунок 6.7). затем лента переносится вперед до тех пор, пока задний конец ее не окажется у закрепленной шпильки. Задний рабочий подает переднему рабочему сигнал «стоп» и крючок заднего конца ленты надевает на шпильку 1; лента вновь укладывается в створе измеряемой линии, положение переднего штриха ленты отмечается новой шпилькой 2, после чего задний рабочий вынимает шпильку 1 и надевает ее на кольцо, а передний рабочий протягивает ленту вперед. После отложения первой ленты у заднего рабочего окажется одна шпилька.

Описанные операции повторяют до конца измерения всей длины линии. Число отложенных лент будет равно числу шпилек, оказавшихся у заднего рабочего. Остаток длины 6-В, называемый домером. Измеряют той же мерной лентой. При этом возможны два случая из