Задачи, решаемые с помощью масштаба

Масштабы планов или карт применяют при решении следующих двух задач:

1. по известной длине S проложения линии местности определить длину S₀ этого проложения на плане, имеющем численный масштаб 1/М

2. по длине S₀ отрезка прямой на плане масштаба 1/М определить величину проложения S на местности.

 

Из формулы (1) можно получить:

 

ü для первой задачи S₀ = S / М (2)

ü для второй задачи S = S₀*М (3)

 

Таким образом, из формул (2) и (3) следует:

 

1. величина S₀ отрезка на плане равна проложению S линии на местности, деленной на знаменатель численного масштаба;

2. длина S проложения линии местности, соответствующая величине S₀ отрезка на плане, равна величине S₀ отрезка, умноженной на знаменатель М численного масштаба.

Пример 1. Длина проложения S = 232м. найти величину S₀ изображения этого проложения на плане масштаба 1: 2000.

По формуле (2) получим S₀ = 232/2000 = 0,116м = 11,6см.

Пример 2. Величина отрезка между двумя точками на плане масштаба 1: 5000 S₀ = 5,6см. Определить длину S этой линии на местности.

По формуле (3) будем иметь S = 2,6см*5000 = 13000см = 130м.

 

Однако приведенный способ определения величин S и S₀ малопроизводителен. Он требует выполнения арифметических действий с именованными числами.

Для ускорения решения задач по определению величин S и S₀ пользуются специальным графическим построением – линейным, а также поперечным масштабом.

 

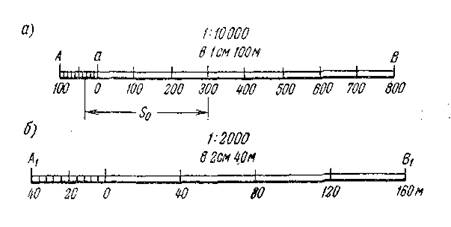
Линейный масштаб

Линейный масштаб строят следующим образом. На прямой АВ (рисунок 2.1)откладывают равные между собой отрезки, называемые основанием масштаба. Обычно длину принимают равной 1 или 2см.

 

 

Рисунок 2.1 – Линейный масштаб

По заданному численному масштабу плана определяют число метров на местности, которому будет соответствовать принятое основание мас­штаба, Так, если за основание масштаба взят 1см, а численный масштаб равен 1: 10 000, то основание линейного масштаба будет соответствовать длине на местности 100м.

Первое основание А-а линейного масштаба (рисунок 2.1а)делят на десять равных частей. Правый крайний штрих а этого основания принимают за нуль — начало счета делений линейного масштаба. Вправо от нуля деления, равные основанию масштаба, выражают соответствующим чис­лом метров. При масштабе 1: 10 000 каждый сантиметр линейного мас­штаба, как уже было сказано, соответствует 100мна местности. Влево от 0 подписывают десятые доли основания, выраженные также в метрах. В рассматриваемом примере каждая десятая доля основания масштаба соответствует 10м.

Поскольку наименьшее расстояние, различимое глазом, равно 0,1мм, то, следовательно, пользуясь линейным масштабом, можно определять расстояния только в пределах до 0,1мм, что в приведенном на рисунке 2.1 примере соответствует одному метру на местности. Эта величина (0,1мм ) и является графической предельной точностью линейного масштаба. Для планов и карт, имеющих численный масштаб 1: 500,, 1: 1000, 1: 5000, 1: 10 000 и т. д., графическая предельная точность масштаба соответственно равна 0,05; 0,1; 0,5 и 1,0м.Это значит, что отрезки линий, меньше указанных, не могут быть выражены на плане или карте данного масштаба.

Линейным масштабом пользуются следующим образом. Если при помощи линейного масштаба, изображенного на рисунке 2.1а, нужно отло­жить на плане отрезок, соответствующий расстоянию 420м на местности, то правую ножку циркуля-измерителя совмещают с делением 400, рас­положенным правее нулевого деления, а левую совмещают со вторым делением основания масштаба, расположенным левее 0. Общий раствор циркуля-измерителя будет соответствовать заданному расстоянию на местности.

Если требуется узнать, какой длине на местности соответствует рас­стояние между двумя точками на плане, то для этого нужно циркулем-измерителем взять это расстояние S₀ на плане. Затем, не меняя раствора циркуля, правую его ножку совмещают с делением правой части линей­ного масштаба так, чтобы левая ножка циркуля разместилась несколько левее 0. Пусть правое деление будет 300и(см. рисунок 2.1а), а левая ножка циркуля расположилась левее нуля и заняла положение между третьим и четвертым делениями основания масштаба (А-а). Тогда расстояние на местности составит 300 + 30 = 330м,причем к этой величине надо еще добавить часть наименьшего деления между третьим и четвертым штри­хами. Эту часть определяют на глаз. Пусть она равна 0,4мм,что соответ­ствует 4м. Таким образом, расстояние S₀между точками на плане соот­ветствует 334мна местности.

Линейный масштаб можно построить и с основанием, равным 2см. На рисунке 2.1бизображен такой масштаб. При условии, если численный масштаб равен 1: 2000, основание линейного масштаба в данном случае будет соответствовать 40мна местности.

 

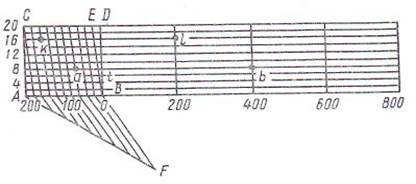
ПОПЕРЕЧНЫЙ МАСШТАБ

Для более точного построения плана или определения длин отрезков пользуются поперечным масштабом (рисунок 2.2).

 

 

 

Рисунок 2.2 – Поперечный масштаб

За основание такого масштаба обычно принимаютотрезок АВ =2см и делят его на 10 равных частей. Для этого под произвольным углом к основа­нию проводят прямую AF и на ней от точки А откладывают 10 произвольных, но равных частей; соединив точки В и F, проводят через все точкилинии AF прямые, параллельные ВF, которые и разделят основание на 10 равных частей. Далее, на линии АС, перпендикулярной АВ откладывают 10 произвольных, но равных между собой отрезковичерез полученные точки проводят линии, параллельные АВ. Отрезки междунаклонными линиями, парал­лельными BE, равны десятым долям основания АВ, т. е. ED = АВ/10

Отрезки, заключенные между перпендикуляром BD и наклонной BE, равны сотым долям основания, т. е. t = ЕD/10 = АВ/10*10 = АВ/100. Такой масштаб называют еще нормальным попереч­ным масштабом.

Цифры, написанные внизу масштаба, изображенного на рисунке 2.2, соответствуют численному масштабу 1:10 000. Тогда основание АВ для такого масштаба соответствует на местности 200м, а наимень­шее деление будет t = 200/10*10 = 2м. Отрезки ab и kl для данного случая будут соответствовать 468 и 356м.

 

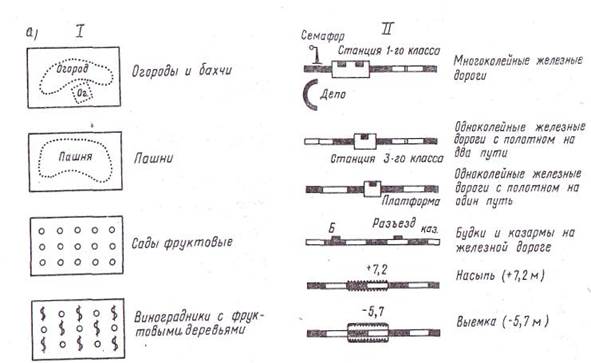
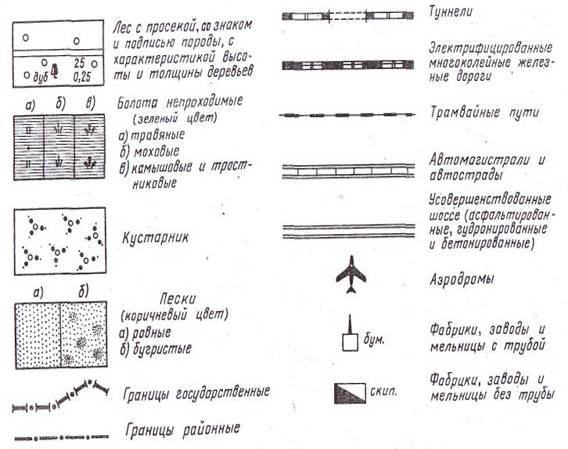
Условные знаки на планах, картах и геодезических чертежах

Для обозначения на планах и картах различных предметов местности применяют специально разработанные условные знаки. Для облегчения пользования планом или картой очертания условных знаков напоминают вид изображаемых элементов местности. Условные знаки для топографических планов и карт являются едины­ми для всей России. В основу создания условных знаков положено единство их начертания, поэтому для чтения планов и карт достаточно изучить условные знаки одного какого-нибудь масштаба.

Некоторую особенность представляют собой условные знаки разбивочных и исполнительных чертежей, которые применяются при проектировании генеральных планов сооружаемых объектов. Условные знаки принято делить на контурные, или масштабные, и внемасштабные.

Масштабными называют условные знаки, которыми предметы местности изображают с соблюдением масштаба карты или плана. Они дают возможность определить по плану или карте не только местоположение предмета, но и его размеры.

 

 

Контрольные вопросы

1.Что называется планом, картой, профилем местности?

2.Что называется масштабом?

3.Что представляют собой численный, линейный и поперечный масштабы?

4.Построить линейный масштаб, если численный равен: 1:500; 1:2000; 1:50 000.

5.Определить цену деления поперечного масштаба, если число делений на основании 10, а численный масштаб 1:500; 1:10000; 1:2500.

 

Приложение

 

 

 

 

 

 

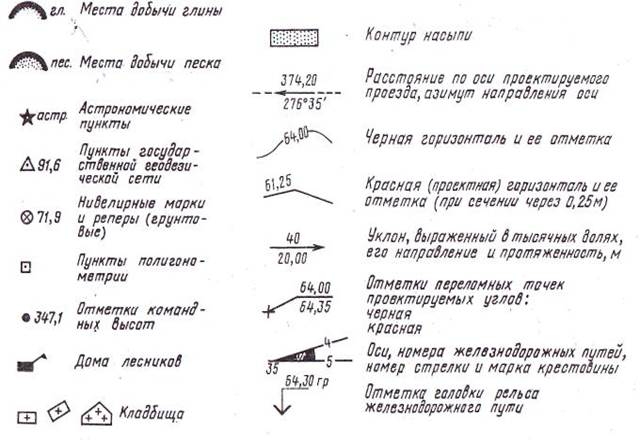
а - для топографических планов (I - масштабные, II - внемасштабные);

б - для геодези­ческих истроительных чертежей

Рисунок 2.3 – Условные знаки

ЛЕКЦИЯ № 3