Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная геодезическая задачаСодержание книги
Поиск на нашем сайте Обратная геодезическая задача состоит в том, что по данным прямоугольным координатам начала и конца отрезка прямой определяют дирекционный угол и длину этого отрезка. Пусть даны координаты точек А и В (рисунок 5.2). необходимо определить длину отрезка АВ – s и величину дирекционного угла αАВ этого отрезка. Из прямоугольного треугольника АаВ имеем: tg αАВ = Принимаем: Ва = ∆ у = уВ – уА Аа = ∆ х = хВ – хА Получим: tg αАВ = Значение длины отрезка АВ может быть вычислено из прямоугольного треугольника АаВ по теореме Пифагора s = При решении обратной задачи для вычисления дирекционного угла пользуются формулой
Примеры решения задач Пример 1. Пусть даны хА = 50,0м, уА = 80,0м, s = 100м, αАВ = 120˚30'. Необходимо вычислить координаты точки В: хВ и уВ. Решение. Вычисления выполняют по следующей схеме. Так как дирекционный угол αАВ больше 90˚, а именно 90˚-180˚, то данный отрезок находится во второй координационной четверти. В расчетах угол αАВ заменяем на румб r. Для второй четверти румб будет равен rAB = 180˚- αАВ = 180˚-120˚30' = 59˚30':ЮВ rAB = 59˚30':ЮВ Так как отрезок АВ находится во второй четверти, знаки приращений будут ∆х (-); ∆у(+), поэтому формулы для вычисления координат точки В хВ и уВ.: хВ = хА - ∆х = хА – s ∙ cos rAB yВ = yА + ∆y = yА – s ∙ sin rAB хВ = 50 – 100 ∙ cos 59˚30' = 50 – 100 ∙ 0,507538 = - 0,754 yВ = yА + ∆y = yА – s ∙ sin 59˚30' = 80 + 100 ∙ 0,861629 = 166,163 Правильность решения задачи можно подтвердить чертежом, выполнив его в масштабе.
Пример 2. Пусть даны прямоугольные координаты точек А и В. Необходимо найти дирекционный угол αАВ и длину линии АВ – s. хА = 20,0м, уА = 30,0м хВ = - 40,0м, уВ = - 60,0м Решение. Приращение координат вычислим по формуле: ∆ у = уВ – уА = - 60 - 30 = -90,0 ∆ х = хВ – хА = - 40 – 20 = - 60,0 Так как знаки приращений отрицательные, то линия лежит в III четверти, где дирекционный угол будет равен: rAB = αАВ - 180˚ => αАВ = 180+ rAB Румб линии rAB находим по формуле: tg rАВ = По таблице находим значение угла для tg rАВ =1,5 => rАВ =56˚19', тогда αАВ = 180˚ + 56˚19' = 236˚19' Длину отрезка АВ находим по формуле: sАВ =
Задачи для самоконтроля: 1. Определить координаты точки В: хВ и уВ ., если длина линии АВ sAB = 120м, координаты точки А хА = - 10,5м, уА = - 22,0м. дирекционный угол линии АВ αАВ = 225˚35'.
2. Определить длину линии DС sDC и ее дирекционный угол αDC, если координаты начальной и конечной точек равны: хD = 22,5м, уD = - 20,0м хC = 10,0м, уC = 30,0м свои решения подтвердить чертежами в масштабе 1:1000
ЛЕКЦИЯ №6 УРОК № 11. ОСНОВНЫЕ СВЕДЕНИЯ ОБ ИЗМЕРЕНИЯХ. Единицы измерения Измерение - есть процесс сравнения какой-либо величины с другой однородной с ней величиной, принятой за единицу измерения. Например, измерение длины отрезка прямой линии путем последовательного укладывания вдоль этой линии мерного прибора есть процесс сравнения двух однородных величин — измеряемой длины отрезка прямой линии с известной длиной другого отрезка прямой, выраженной в единицах измерения. В геодезии за единицу длины обычно принимают метр., Метр (в переводе сгреческого значит «мера») — одна из основных единиц Международной системы единиц СИ (Международная система единиц СИ введена в действие с 1 января 1963г. ГОСТом 9867-61). С 1889 г. было принято следующее определение метра: единица длины — метр определяется расстоянием (при 0° С и нормальном относительном давлении) между осями двух средних штрихов, нанесенных на платино-иридиевом бруске, хранящемся в Международном бюро мер и весов и служащем прототипом метра, длина которого соответствует одной десятимиллионной части Парижского меридиана (эллипсоид Деламбра). По штрихам, нанесенным на этом прототипе, можно производить сличение других эталонов метра с точностью в пределах от одной до двух десятых микрона.. Однако для научных целей такая точность в наше время является недостаточной. Поэтому XI Генеральная конференция по мерам и весам (1960 г.) утвердила новый естественный и неуничтожаемый эталон метра, выраженный через длину световых волн, и установила новое определение метра: Метр - длина, равная 1650763,73 длин волн в вакууме излучения, соответствующего переходу между уровнями 2р10 и 5d5 атома криптона 86.
Международной системой единиц (СИ) установлена также единица плоского угла – радиан (рад). Радиан - угол между двумя радиусами круга, вырезающий на окружности дугу, длина которой равна радиусу. Для измерения плоских углов применяют другие, более мелкие единицы — градус, минуту, секунду. Один градус представляет собой 1/360 длины окружности, или
1 градус (О) = 2πR/360 = πR/180
Поскольку длина радиуса R соответствует радиану (рад), можно написать: 1 градус (О) = (π/180) рад = 1,75 * 10-2 рад; 1 минута (') = (π/180*60) рад = 2,91 * 10-4 рад; 1 секунда (") = (π/180*60*60) рад = 4,85 * 10-6 рад; 1 радиан (рад)= 57° 17 ' 44 ",8 = 3437 ', 7 = 206 264 ",8.
|
||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 5518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.005 с.) |

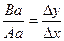

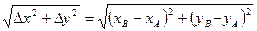
 , причем в результате вычислений будет найден острый угол (румб). Чтобы по румбу определить величину дирекционного угла нужно сначала выяснить, к какой четверти относится этот угол, что зависит от знаков приращений ∆х и ∆у (см. табл.5.1)
, причем в результате вычислений будет найден острый угол (румб). Чтобы по румбу определить величину дирекционного угла нужно сначала выяснить, к какой четверти относится этот угол, что зависит от знаков приращений ∆х и ∆у (см. табл.5.1)