Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие случайных величин и их видыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тема 5. Случайные дискретные величины (ДСВ) План: 1. Понятие случайной величины и их виды 2. Закон распределения ДСВ. 3. Биномиальное распределение, 4. Геометрическое распределение 5. Числовые характеристики и свойства ДСВ 6. Функция распределения ДСВ Теоретические сведения Понятие случайных величин и их виды Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение. Это значение не известное и оно зависящее от некоторых случайных причин, которые заранее не могут быть учтены. Примеры случайных величин: 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: О, 1, 2,.... 100. 2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, Ь). 3. Урожайность любой культуры есть случайная величина, которую трудно прогнозировать, но эта величина находится в некотором интервале в зависимости от региона и культуры, а также иных причин. 4. Оценка на экзамене по теории вероятностей, в принципе случайная величина, принимающая значения 1,2,3,4.5. 5. Число принявшихся саженцев из купленных 10 штук.
Случайные величины обозначаются буквами латинского алфавита, например X,Y, Z. Их возможные значения обозначаются соответствующими строчными буквами x,y z. с индексами внизу Случайные величины делятся на дискретные и непрерывные величины Случайной дискретной величиной являетсявеличина, значения которой отделены одно от другого промежутками, в которых нет возможных значений этой величины. Случайная величина при этом принимает отдельные, изолированные возможные значения. Примеры 1, 4,5. Случайной непрерывной величиной является величина, которая может принять любое из значений некоторого промежутка. Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины. Непрерывная случайная величина, принимать все свои значения из некоторого конечного или бесконечного промежутка. Число возможных значений случайной дискретной величины может быть конечным или бесконечным. Примеры 2,3. Закон распределения ДСВ При рассмотрении случайных дискретных величин правомочен вопрос о вероятности появления каждого своего значения. Законом распределения случайной дискретной величиныназывают соответствие между возможными значениями и их вероятностями. Закон распределениячаще всего задается табличным способом. Возможно его задание графическим или аналитическим (в виде формулы) способами.
При табличном задании - первая строка таблицы содержит возможные значения, а вторая - их вероятности. См таблицу. Значения величины образуют полную группу, причем сумма их вероятностей равна единице p1+ p2 +…+ pn =1. Задание 5-1. Найти закон распределения 1. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по I руб. Найти закон распределения случайной величины X - стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение. Напишем возможные значения X: х1=50, x2= I, x3 = 0. Вычислим соответствующие им вероятности. Всего было 100 билетов, среди них один билет в 50 рублей, поэтому р1 = 1/100=0,01 и 10 билетов по 1 рублю, значит р2 = 10/100=0,1, p3=l- (0,01 + 0,1) = 0,89. Ответ Закон распределения: записан в виде таблицы Контроль: 0,01+0,1+0,89=1.
2. В новогодней школьной лотереи лотерее разыгрывается 1 книга, 10 игрушек, 100 открыток. Найти закон распределения случайной величины X для владельца одного билета. Биномиальное распределение, Производится п независимых испытаний, в каждом из которых событие А появиться либо не появиться. Положим, что вероятность наступления события во всех испытаниях постоянна и равна p. Зададимв этих испытаниях. случайную дискретную. величину X - число появлений события A и для нее установим закон распределения Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза,.... либо п раз. Таким образом, возможные значения X таковы: xi = 0,1,2,… n. Вероятности этих возможных значений определяются по формуле Бернулли.
Указанная формула является аналитическим выражением искомого закона распределения. Полученное распределение называется б иномиальным распределением вероятностей ввиду того, что эту формулу можно рассматривать как общий член разложения бинома Ньютона: Задание 5-2. Найти закон распределения случайной величины по формуле Бернулли. 1. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X - числа выпадений "герба".
Решение. Вероятность появления "герба" в каждом бросании монеты р=1/2, следовательно, вероятность не появления герба 9=1-1/2 = 1/2.
2. По мишени проводится 4 выстрела с вероятностью попадания 0,8. Найти закон распределения случайной величины Х – число попаданий в мишень. Решение. Возможные значения случайной величины х=0,1,2,3,4. Всего 5 значений. соответствующие им вероятности находятся по формуле Бернулли: р0 =С40·0,80·0,24=0,0016. Аналогично находятся остальные вероятности.
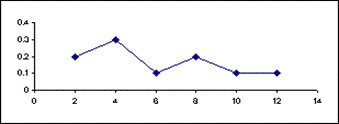
Для наглядности закон распределения случайной дискретной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (Xi, Pi ), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. Он представлен на рисунке. 3. Используя ответы в предыдущем задании, найти вероятности события 1 ≤ х ≤ 3 и вероятность события х ³ 3 Р(1 ≤ х ≤ 3) = Р(1,2,3) = 0,0256 +0,0536+0,4096 = 0,5888 и Р(х ³ 3) = Р(4)= 0,4096 4. В ящике 7 шаров, из них белых - 4, черных -3. Извлекается наудачу 3 шара. Найти закон распределения случайной величины Х – число извлеченных белых шаров.
Распределение Пуассона При рассмотрении случайной дискретной величины в которой число значения этой величины очень велико. то воспользоваться формулой Бернулли затруднительно. В таких случаях используется распределение Пуассона, когда подсчет вероятности производится по формуле Пуассона, а такое распределение называется распределением Пуассона Формула Пуассона имеет вид Эта формула выражает закон распределения Пуассона вероятностей массовых (п велико) и редких (р мало) событий. Замечание. Имеются специальные таблицы, пользуясь которыми можно найти Pn(k), зная k и λ. Задание 5-3. Записать распределение Пуассона. 1. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут три негодных изделия. Решение. n=5000, р= 0,0002, k = 3. λ = np = 5000 -0.0002=1. По формуле Пуассона искомая вероятность приближенно равна P5000(3)=(13 : 3! ) ·e-1 =1:6e=0,06 Задание 5-6. 1. Найти математическое ожидание случайной величины X, зная закон ее распределения: X 3 5 2 р 0,1 0,6 0,3 Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности: М(Х) =-3·0,1+5·0,6 + 2·0,3 = 3,9. 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р. Решение. Случайная величина X ="Число появлений события А в одном испытании" может принимать только два значения: х1= 1 (событие А наступило) с вероятностью р и хг =0 (событие А не наступило) с вероятностью q = I - р. Искомое математическое ожидание равно М (X) = 1·p+ 0·q =p.
Математическое ожидание числа появлений события в одном испытании равно вероятности этого события. Этот результат будет использован в дальнейшем. Вероятностный смысл математического ожидания приближенно равно среднему арифметическому наблюдаемых значений случайной величины, причем, чем больше число испытаний, тем точнее результат. Легко установить, что математическое ожидание больше наименьшего и меньше наибольшего из возможных значений. Другими словами, на числовой оси возможные значения расположены слева и справа от математического ожидания. Ввиду того, что математическое ожидание характеризует расположение распределения, его часто называют центром распределения. Про математическое ожидание можно сказать, что это есть абсцисса центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы - их вероятностям, Происхождение термина "математическое ожидание" связываются с начальным периодом применения теории вероятностей в области азартных игр (XVI - XVII вв.), Игрока интересовало среднее значение ожидаемого выигрыша, или математическое ожидание выигрыша. Задание 5-8. 1. Найти математическое ожидание случайной дискретной величины, зная закон ее распределения: X 6 3 1 р 0,2 0,3 0,5 Ответ: 2,6. 2. Производится 4 выстрела. Вероятность попадания каждого в цель равна 0,6; 0,2; 0.4; 0.5; 0,7. Найти математическое ожидание общего числа попаданий. Ответ: 2,2 попадания. 4. Независимые случайные дискретные величины заданы законами распределения: Х 1 2 Y 0,5 1 р 0,2 0,8 р 0,3 0,7 Найти математическое ожидание произведения XY двумя способами: а) составив закон распределения XY; б) пользуясь свойством 3. Ответ: 1,53. 4. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 10 деталей. Ответ: 2 детали. 5. Найти математическое ожидание произведения числа очков, которые могут выпасть при одном бросании двух игральных костей. Ответ: 12,25 очка. 6. Найти математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов. Вероятность выигрыша по одному билету равна 0,3. Ответ: 6 билетов. Задание 5-9.
Решение. Математическое ожидание М(Х)=1·0,2+2·0,8 =1,8 Отклонения равны: 1 - 1,8 = -0,8; 2-1,8 = 0,2. Математическое ожидание отклонения: М [X - М(Х)] = -0,8·0,2+ 0,2-0,8 = 0. Теорема. Математическое ожидание отклонения равно нулю Это следует из следующих рассуждений. Учитывая, что математическое ожидание разности равно разности математических ожиданий и то, что математическое ожидание постоянной равно самой постоянной), а также учитывая, что М (X) - постоянная величина, имеем: М [X - М (X)] = М (X) - М [М (X)] = М (X) - М (X) = 0.
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена. На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е. М [X - М (X)], для любой случайной величины равно нулю. Это свойство уже было рассмотрено в предыдущем параграфе и объясняется тем, что одни возможные отклонения положительны, а другие - отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Дисперсия - среднее значение квадрата отклонения, Дисперсией (рассеянием) случайной дискретной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: Для того чтобы найти дисперсию, достаточно вначале вычислить все возможные произведения значений квадрата отклонения, а затем эти произведения сложить. Замечание. Из определения следует, что дисперсия случайной дискретной величины есть неслучайная (постоянная) величина. Вычисление, выполненное на основе определения дисперсии относительно громоздкие. Открыта формула, которая приводит к определению дисперсии значительно быстрее. Теорема. Дисперсия ровна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания: D(Х)= М(Х2)-(М(Х))2 Задание 5-10. 1. Вычислить дисперсию на основе определения дисперсии
Решение. Математическое ожидание М(Х)= 1-0,3 + 2-0,5 + 5-0,2 = 2,3. Квадраты отклонений: (1 - 2,3)2 = 1,69; (2 - 2,3)2 = 0,09; (5- 2,3)2 = 7,29. Закон распределения квадрата отклонения:
Дисперсия D(Х)= I,69.0,3+0,09-0,5 + 7,29·0,2 = 2,01. 2. Вычислить дисперсию по формуле. Найти дисперсию случайной величины X, которая задана законом распределения в виде таблицы.:
М(Х) = 2- 0,1+3-0,6 + 5-0,3 = 3,5.
Математические ожидания М(Х2) = 4- 0,1 +9-0,6 + 25-0,3= 13,3. Дисперсия равна D(X)=M (XZ)-[M (X)]2 = 13,3- (3,5)2= 1,05. Замечание. Если величины X и Y имеют возможные одинаковые значения и одно и то же математическое ожидание, то их дисперсии не всегда равны, хотя ведь возможные значения обеих величин одинаково рассеяны вокруг своих математических ожиданий. Это связано с тем, что возможные одинаковые значения рассматриваемых величин имеют, вообще говоря, различные вероятности, а величина дисперсии определяется не только самими возможными значениями, но и их вероятностями. Выскажем утверждение. Е сли вероятности "далеких" от математического ожидания возможных значений X больше, чем вероятности этих же значений Y, и вероятности "близких" значений X меньше, чем вероятности тех же значений Y, то, очевидно, дисперсия X больше дисперсии Y.
Задание 5-11. И ллюстрирующий пример, выше приведенного утверждения Сравните дисперсии случайных величин, заданных законами распределения: X - 1 1 2 3 Y - I 1 2 3 р 0,48 0,01 0,09 0,42 р 0,19 0,51 0,25 0,05 Решение. М(Х)=М(Y)=0,97. D(X)= 3,69; D (Y)= 1,21. Таким образом, возможные значения и математические ожидания X и Y одинаковы, а дисперсии различны, причем D (X) > D (Y). Этот результат можно было предвидеть без вычислений, глядя лишь на законы распределений. Свойства дисперсии Свойство 1. Дисперсия постоянной величины равна нулю: D (С)=0 Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX)-C2 ·D(X). Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D (X + Y) = D (X) + D (У) Следствия 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин. 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины: Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:D (X - Y) = D (X) + D (У) Задание 5-12..
1. Вычислить дисперсии случайной величины, по ее закону распределения: Решение. М(Х)=3,1; М(Х2)=10,9; D(X)=10,9-3,12=1,29 2. Дисперсия случайной величины X равна 3. Найти дисперсию величин: K= -5X и S= 4X+5. Решение. D(K)= D(-5·X)=(-5)2·D(X)=25·3=75 D(S)= D(4X+5)= D(4X)+D(5)= 42·D(X)+ D(5) =16·3 +0=48 Функция распределения ДСВ Случайная дискретная величина может быть задана перечнем всех ее возможных значений и их вероятностей. Такой способ задания не является общим: он неприменим, например, для случайных непрерывных величин. Действительно, рассмотрим случайную величину X, возможные значения которой сплошь заполняют интервал (а, b). Можно ли составить перечень всех возможных значений X? Очевидно, что этого сделать нельзя. Этот пример указывает на целесообразность дать общий способ задания любых типов случайных величин. С этой целью и вводят функции распределения вероятностей случайной величины. Пусть x - действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее x, т. е. вероятность события X < х, обозначим через F(x). Разумеется, если х изменяется, то, изменяется и F(x). Итак, F (x) - функция от х. Функцией распределения называют функцию F(х), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, или F(х)=P(X<x) С геометрической точки зрения F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х. Иногда вместо термина "функция распределения" используют термин "интегральная функция". Теперь можно дать более точное определение случайной непрерывной величины. Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. Практические замятия. 1. Решение задач на запись распределение ДСВ, 2. Вычисление характеристик и функций от ДСВ на основе свойств. Контрольная работа Теория вероятностей, ДСВ
Вариант 1 Задан закон распределения ДСВ, представленный в виде таблицы:
1.Построить график закона распределения 2. Вычислить математическое ожидание, дисперсию, квадратичное отклонение. 3. Составить функцию распределения и построить ее график.
Ответ
Контрольная работа Теория вероятностей, ДСВ Вариант 2 Задан закон распределения ДСВ, представленный в виде таблицы:
1.Построить график закона распределения 2. Вычислить математическое ожидание, дисперсию, квадратичное отклонение. 3. Составить функцию распределения и построить ее график.
Ответ
Требования к знаниям умениям и навыкам Студент должен иметь представление о ДСВ, ее распределении и графичёском ее изображении. Иметь представление о функции от ДСВ и знать методику записи распределения функции от одной и двух ДСВ. Знать: определение математического ожидания, дисперсии ДСВ, среднеквадратического отклонения ДСВ и их свойства. Иметь представление о биномиальном распределении и знать формулы для вычисления его характеристик. Иметь представление о геометрическом распределении.
Тема 5. Случайные дискретные величины (ДСВ) План: 1. Понятие случайной величины и их виды 2. Закон распределения ДСВ. 3. Биномиальное распределение, 4. Геометрическое распределение 5. Числовые характеристики и свойства ДСВ 6. Функция распределения ДСВ Теоретические сведения Понятие случайных величин и их виды Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение. Это значение не известное и оно зависящее от некоторых случайных причин, которые заранее не могут быть учтены. Примеры случайных величин: 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: О, 1, 2,.... 100. 2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, Ь). 3. Урожайность любой культуры есть случайная величина, которую трудно прогнозировать, но эта величина находится в некотором интервале в зависимости от региона и культуры, а также иных причин. 4. Оценка на экзамене по теории вероятностей, в принципе случайная величина, принимающая значения 1,2,3,4.5. 5. Число принявшихся саженцев из купленных 10 штук.
Случайные величины обозначаются буквами латинского алфавита, например X,Y, Z. Их возможные значения обозначаются соответствующими строчными буквами x,y z. с индексами внизу Случайные величины делятся на дискретные и непрерывные величины Случайной дискретной величиной являетсявеличина, значения которой отделены одно от другого промежутками, в которых нет возможных значений этой величины. Случайная величина при этом принимает отдельные, изолированные возможные значения. Примеры 1, 4,5. Случайной непрерывной величиной является величина, которая может принять любое из значений некоторого промежутка. Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины. Непрерывная случайная величина, принимать все свои значения из некоторого конечного или бесконечного промежутка. Число возможных значений случайной дискретной величины может быть конечным или бесконечным. Примеры 2,3. Закон распределения ДСВ При рассмотрении случайных дискретных величин правомочен вопрос о вероятности появления каждого своего значения. Законом распределения случайной дискретной величиныназывают соответствие между возможными значениями и их вероятностями. Закон распределениячаще всего задается табличным способом. Возможно его задание графическим или аналитическим (в виде формулы) способами.
При табличном задании - первая строка таблицы содержит возможные значения, а вторая - их вероятности. См таблицу. Значения величины образуют полную группу, причем сумма их вероятностей равна единице p1+ p2 +…+ pn =1. Задание 5-1. Найти закон распределения 1. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по I руб. Найти закон распределения случайной величины X - стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение. Напишем возможные значения X: х1=50, x2= I, x3 = 0. Вычислим соответствующие им вероятности. Всего было 100 билетов, среди них один билет в 50 рублей, поэтому р1 = 1/100=0,01 и 10 билетов по 1 рублю, значит р2 = 10/100=0,1, p3=l- (0,01 + 0,1) = 0,89. Ответ Закон распределения: записан в виде таблицы Контроль: 0,01+0,1+0,89=1.
2. В новогодней школьной лотереи лотерее разыгрывается 1 книга, 10 игрушек, 100 открыток. Найти закон распределения случайной величины X для владельца одного билета. Биномиальное распределение, Производится п независимых испытаний, в каждом из которых событие А появиться либо не появиться. Положим, что вероятность наступления события во всех испытаниях постоянна и равна p. Зададимв этих испытаниях. случайную дискретную. величину X - число появлений события A и для нее установим закон распределения Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза,.... либо п раз. Таким образом, возможные значения X таковы: xi = 0,1,2,… n. Вероятности этих возможных значений определяются по формуле Бернулли.
Указанная формула является аналитическим выражением искомого закона распределения. Полученное распределение называется б иномиальным распределением вероятностей ввиду того, что эту формулу можно рассматривать как общий член разложения бинома Ньютона: Задание 5-2. Найти закон распределения случайной величины по формуле Бернулли. 1. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X - числа выпадений "герба".
Решение. Вероятность появления "герба" в каждом бросании монеты р=1/2, следовательно, вероятность не появления герба 9=1-1/2 = 1/2.
2. По мишени проводится 4 выстрела с вероятностью попадания 0,8. Найти закон распределения случайной величины Х – число попаданий в мишень. Решение. Возможные значения случайной величины х=0,1,2,3,4. Всего 5 значений. соответствующие им вероятности находятся по формуле Бернулли: р0 =С40·0,80·0,24=0,0016. Аналогично находятся остальные вероятности.
Для наглядности закон распределения случайной дискретной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (Xi, Pi ), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. Он представлен на рисунке. 3. Используя ответы в предыдущем задании, найти вероятности события 1 ≤ х ≤ 3 и вероятность события х ³ 3 Р(1 ≤ х ≤ 3) = Р(1,2,3) = 0,0256 +0,0536+0,4096 = 0,5888 и Р(х ³ 3) = Р(4)= 0,4096 4. В ящике 7 шаров, из них белых - 4, черных -3. Извлекается наудачу 3 шара. Найти закон распределения случайной величины Х – число извлеченных белых шаров.
Распределение Пуассона При рассмотрении случайной дискретной величины в которой число значения этой величины очень велико. то воспользоваться формулой Бернулли затруднительно. В таких случаях используется распределение Пуассона, когда подсчет вероятности производится по формуле Пуассона, а такое распределение называется распределением Пуассона Формула Пуассона имеет вид Эта формула выражает закон распределения Пуассона вероятностей массовых (п велико) и редких (р мало) событий. Замечание. Имеются специальные таблицы, пользуясь которыми можно найти Pn(k), зная k и λ. Задание 5-3. Записать распределение Пуассона. 1. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут три негодных изделия. Решение. n=5000, р= 0,0002, k = 3. λ = np = 5000 -0.0002=1. По формуле Пуассона искомая вероятность приближенно равна P5000(3)=(13 : 3! ) ·e-1 =1:6e=0,06
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 2609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.52.29 (0.011 с.) |

 , где n - число исходов, k =0,1,2,…n, p - вероятность наступления события, q - вероятность не наступления события (q =1-p)
, где n - число исходов, k =0,1,2,…n, p - вероятность наступления события, q - вероятность не наступления события (q =1-p) При двух бросаниях монеты "герб" может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X: 0,1,2.. Найдем вероятности этих возможных значений по формуле Бернулли. Контроль: 0,25+0,5+0,25=1.
При двух бросаниях монеты "герб" может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X: 0,1,2.. Найдем вероятности этих возможных значений по формуле Бернулли. Контроль: 0,25+0,5+0,25=1.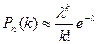 , где
, где  .
. 1. Задан закон распределения случайной дискретной величины X. Вычислить математическое ожидание отклонения
1. Задан закон распределения случайной дискретной величины X. Вычислить математическое ожидание отклонения Найти дисперсию случайной величины, которая задана законом распределения, представленным в таблице.
Найти дисперсию случайной величины, которая задана законом распределения, представленным в таблице.
 Решение.
Решение.