
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики случайных величин и случайных функций.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Случайной величиной называется такая величина, которая в результате опыта может принимать различные заранее не известные численные значения при сохранении определенной совокупности условий, сопровождающий данный опыт. Одни случайные величины могут принимать отдельные друг от друга изолированные числовые значения. Такие случайные величины называются дискретными или прерывными. Числовые характеристики случайных величин. 1)Математическое ожидание (среднее значение).Определение: Математическим ожиданием называется- для дискретной случайной величины: Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания) - для непрерывной случайной величины:
-для непрерывной случайной величины: Дисперсией случайной величины х называется математическое ожидание квадрата отклонения значения величины от ее математического ожидания: Dx = M(x-Mx)2 - для дискретной случайной величины:
28)Измерения и наблюдения. Классификация измерения.Дискретные – это такие измерения которые выполняются через определённый интервал времени.Непрерывные – это те измерения которые ведутся всегда автоматизированными аппаратами.Необходимые – это измерения минимальное количество которых обеспечивает.Избыточные – это такие которые выполнены сверх необходимых.Равноточные – это такие СКП результат измерения которых будет одинаковый.По степени взаимо связи:взаимонезависимы – измерение погрешности которой формируется различными факторами.корреляционновзаимозависимы – это измерения в состав погрешности которых входит одна и та же общая погрешность сформирована одним и тем же фактором.Функциональнозависимы – это измерения все погрешности которых формируются одним и тем же фактором.. 29)Классификация погрешности и их свойства. Методы учёта систематических погрешностей.Погрешность измерения называется разница между измеренным и истинным значением величины.Непосредственно источник погрешности является:несовершенство приборов и инструментов,несовершенство органов чувств и не стабильность психического состояния,незакономерные колебания параметров внешней среды,нестабильность метода измерений, несовершенство метода измерений.По характеру действия на величину погрешности подразделяются на:случайные, Систематические. систематические на: Постоянные,Переменные,периодические,прогрессивные,грубые (промахи).
|
||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.107.11 (0.009 с.) |


 Интеграл должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания).Свойства математического ожидания:a. Если С - постоянная величина, то МС = С, b. МСх = СМх, c. Математическое ожидание суммы случайных величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + Мy, d. Вводится понятие условного математического ожидания. Если случайная величина принимает свои значения хi с различными вероятностями p(xi/Hj) при разных условиях Hj, то условное математическое ожидание определяется как
Интеграл должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания).Свойства математического ожидания:a. Если С - постоянная величина, то МС = С, b. МСх = СМх, c. Математическое ожидание суммы случайных величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + Мy, d. Вводится понятие условного математического ожидания. Если случайная величина принимает свои значения хi с различными вероятностями p(xi/Hj) при разных условиях Hj, то условное математическое ожидание определяется как или
или  Если известны вероятности событий Hj, может быть найдено полное математическое ожидание:
Если известны вероятности событий Hj, может быть найдено полное математическое ожидание: Если f(x) - есть функция случайной величины х, то определено понятие математического ожидания функции случайной величины: - для дискретной случайной величины:
Если f(x) - есть функция случайной величины х, то определено понятие математического ожидания функции случайной величины: - для дискретной случайной величины: Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся.
Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся. Интеграл должен быть абсолютно сходящимся. 2. Дисперсия случайной величины. Определение:
Интеграл должен быть абсолютно сходящимся. 2. Дисперсия случайной величины. Определение: Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)- для непрерывной случайной величины:
Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)- для непрерывной случайной величины: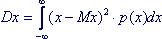 Интеграл должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии).Свойства дисперсии:a. Если С - постоянная величина, то DС = 0, b. DСх = С2Dх, c. Дисперсия суммы случайных величин всегда равно сумме их дисперсий только, если эти величины независимы (определение независимых величин), d. Для вычисления дисперсии удобно использовать формулу: Dx = Mx2 - (Mx)2
Интеграл должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии).Свойства дисперсии:a. Если С - постоянная величина, то DС = 0, b. DСх = С2Dх, c. Дисперсия суммы случайных величин всегда равно сумме их дисперсий только, если эти величины независимы (определение независимых величин), d. Для вычисления дисперсии удобно использовать формулу: Dx = Mx2 - (Mx)2


