
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула косинуса угла и синусов
Формула косинуса угла связывает три угла и сторону сферического треугольника, удобна для нахождения неизвестной стороны или угла, противолежащего этой стороне, и читается так: «косинус угла сферического треугольника равен отрицательному произведению косинусов двух других углов плюс произведение синусов этих углов на косинус стороны между ними». С*sinA=a*sinc; 6)Формулы пяти элементов и котангенсов. Формула котангенсов (4-х рядом лежащих элементов) связывает 4 рядом лежащих элемента, используется для нахождения крайних элементов и читается следующим образом: "произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов ".
Синус сторон х на косинус прилежащего угла равен произведению косинуса стороны на синус 3-ей стороны минус произведению синуса противолежащей стороны на косинус 3-ей стороны и на косинус угла между ними. 7) Решение прямоугольных сферических треугольников. Правило Модюи-Непера. Дополнительные формулы для решение косоугольных сферических треугольников. Прямоугольным называется такой сферический треугольник, у которого один из углов равен 90°. Прямоугольные сферические треугольники более рационально решать по правилам Модюи-Непера:в прямоугольном сферическом треугольнике косинус любого среднего элемента равен произведению котангенсов крайних смежных с ним элементов; косинус отдельно лежащего элемента сферического треугольника равен произведению синусов двух не смежных с ним рядом лежащих элементов. Примечание: в обоих правилах принято, что катеты лежат рядом друг с другом и что вместо катетов надо брать их дополнения до 90°, изменяя соответственно наименования тригонометрических функций.
8)Фигура и размеры Земли. Земля представляет собой неправильной формы шар. Длина его экваториального радиуса равна 6 378 245 м. а полярного—6 356 863 м. Как видно, экваториальный диаметр Земли длиннее полярного примерно на 42,8 км. Если изобразить отклонение формы Земли от шара на глобусе с поперечником в 1 м по экватору, то его полярная ось будет короче экваториальной на 3,35 мм. Фигура Земли имеет форму геоида, что переводится как «землеподобный». Геоидом называется фигура, ограничивающая невозмущённую поверхность уровня мирового океана, мысленно проходит под материками и островами, таким образом, что она в каждой своей точке перпендикулярна отвесной линии и имеющая неправильную геометрическую форму. Геометрия геоида очень сложна, поэтому вместо геоида при решении штурманских задач используют более простые модели Земли: эллипсоид вращения, сферу, карту. Размеры референц-эллипсоида Красовского: большая полуось а=6378245 м; в=6356863 м; полярное сжатие а=(а-в)/а=1/298,3; эксцентриситет е=0,0818;R=6371110м.
9)Основные элементы на поверхности небесной сферы и земного сфероида. Плоскость истинного меридиана наблюдателя пересекается с плоскостью истинного горизонта по линии N — S, которая называется полуденной линией, так как в этой плоскости Солнце бывает точно в полдень.
Эта ось пересекается с поверхностью Земли в двух точках, которые называются географическими полюсами: один Северным (С), а другой Южным (Ю). Северным называется тот полюс, в котором, если смотреть на него сверху, вращение Земли направлено против хода часовой стрелки. Противоположный полюс называется Южным. Через любую точку на земном шаре можно провести бесчисленное множество больших и малых кругов.Большим называется круг, образованный на земной поверхности плоскостью сечения, проходящей через центр Земли. Малым называется круг, образованный на земной поверхности плоскостью сечения, не проходящей через центр Земли. Большой круг, плоскость которого перпендикулярна оси вращения Земли, называется экватором. Экватор делит земной шар на Северное и Южное полушария. Малый круг, плоскость которого параллельна плоскости экватора, называется параллелью. Через каждую точку на земной поверхности можно провести только, одну параллель, которая называется параллелью места. Большой круг, проходящий через полюсы Земли, называется географическим, или истинным меридианом. Через каждую точку на земной поверхности, кроме полюсов, можно провести только один меридиан, который называется меридианом места. Меридиан, проходящий через Гринвичскую астрономическую обсерваторию, находящуюся в Англии вблизи Лондона, принят по международному соглашению в качестве начального меридиана.Начальный меридиан делит земной шар на Восточное и Западное полушария. Плоскость экватора и плоскость начального меридиана являются основными плоскостями, от которых производится отсчет географических координат. Системы координат Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющий положение конкретной точки, называется координатами этой точки.В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). Смотри географические координаты.В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае.
11)Радиусы кривизны параллели, меридиана и нормального сечения. Через произвольную точку на поверхности земного эллипсоида можно провести бесчисленное множество вертикальных плоскостей, которые образуют с поверхностью эллипсоида нормальные сечения. Два из них: меридианное и перпендикулярное ему сечение первого вертикала — носят название главных нормальных сечений. Кривизна поверхности земного эллипсоида в разных ее точках различна. Более того, в одной и той же точке все нормальные сечения имеют разную кривизну. Радиусы кривизны главных нормальных сечений в данной точке являются экстремальными, т. е. наибольшими и наименьшими среди всех остальных радиусов кривизны нормальных сечений. Величины радиусов кривизны меридиана М и первого вертикала N в данной широте φ определяются по формулам:M = a(1-e²) / (1 - e²*sin² φ)3/2; N = a / (1 - e²*sin² φ)½ Радиус кривизны r произвольной параллели эллипсоида связан с радиусом кривизны сечения первого вертикала соотношением r = N cos φ.Величины радиусов кривизны главных сечений эллипсоида М и N характеризуют его форму вблизи данной точки. Для произвольной точки поверхности эллипсоида отношение радиусов M / N = 1 - e² / 1 - e²*sin² φ 12)Длина дуг параллели и меридианов. Зная радиус Земли, можно рассчитать длину большого круга (меридиана и экватора); L = 2pR = 2. 3,14 • 6371»40000 км. Определив длину большого круга, можно найти длину дуги меридиана (экватора) в 1° или в 1¢:1° дуги меридиана (экватора) = L/360°= 111 км,1¢ дуги меридиана (экватора) 111/60¢ = 1,853 км.Длина каждой параллели меньше длины экватора и зависит от широты места.
Она равна L пар= L экв соsj пар.Положение точки на поверхности земного эллипсоида может быть определено геодезическими координатами - геодезической широтой и геодезической долготой. Для определения положения точки на поверхности геоида используются астрономические координаты, получаемые путем математической обработки результатов астрономических измерений. Однако в ряде случаев, когда не нужно учитывать разности геодезических и астрономических координат, для определения положения точки в самолетовождении пользуются понятием географические координаты.Географической широтой j называется угол между плоскостью экватора и нормалью к поверхности эллипсоида в данной точке. Широта измеряется от плоскости экватора к полюсам от 0 до 90° к северу или югу. Северная широта считается положительной, южная - отрицательной. 13)Преобразование координат. Преобразованием системы координат называется переход от одной системы координат к другой.При такой замене надо установить формулы, позволяющие по известным координатам точки в одной системе координат определить ее координаты в другой. Главной целью преобразования координат является определение такой координатной системы, в которой уравнение данной линии становится наиболее простым. Удачным расположением координатных осей можно добиться того, чтобы уравнение кривой приняло наиболее простой вид. Это имеет важное значение для исследования свойств кривой. 14)Геодезическая линия. Прямая и обратная геодезическая задача. Геодезическая линия, кривая, главные нормали всех точек которой совпадают с нормалями поверхности, на которой та расположена. Кратчайшее расстояние между двумя точками по поверхности - Г. линия, но не всегда обратно.Геодезическая задача, связана с определением взаимного положения точек земной поверхности и подразделяется на прямую и обратную задачу. Прямой Г. з. называют вычисление геодезических координат — широты и долготы некоторой точки, лежащей на земном эллипсоиде, по координатам др. точки и по длине и азимуту геодезической линии, соединяющей эти точки. Обратная Г. з. заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и азимута геодезической линии между этими точками 15)Сближение меридианов.Сближение меридианов в некоторой точке земного эллипсоида — угол gs между касательной к меридиану этой точки и касательной к эллипсоиду, проведённой в той же точке параллельно плоскости некоторого начального меридиана. С. м. gs является функцией разности долгот l указанных меридианов, широты В точки и параметров эллипсоида. Приближённо С. м. выражается формулой gs = lsin В. С. м. на плоскости геодезической проекции, или картографической проекции (или гауссово С. м.) — это угол g, который образует касательная к изображению какого-либо меридиана с первой координатной осью (абсцисс) данной проекции, являющейся обычно изображением среднего (осевого) меридиана отображаемой территории.
16)Общий принцип изображения поверхностей развёртыванием. РАзвертыванием одной поверхности на другую при помощи изгибания называется такое преобразование первой поверхности, при котором сохраняются элементы её внутренней геометрии.т.е углы. ПЛОЩАДИ, гАУССОВА кривизна поверхности, а так св-во кратчайших линий оставаться кратчайшими.Радиусы кривизны гл. нормальных сечений называются гл. радиусами кривизны в данной точке поверхности..R=1/R1*R2- гауссовая кривизна поверхности
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.199.162 (0.015 с.) |
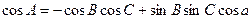 ;
; 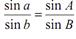


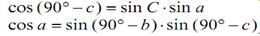

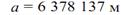
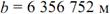
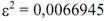
 Вертикальную плоскость, проходящую через глаз наблюдателя перпендикулярно плоскости истинного меридиана наблюдателя, называют плоскостью первого вертикала (плоскость 3). Она пересекается с плоскостью истинного горизонта наблюдателя по линии Ost—W. Таким образом, пересечение взаимно перпендикулярных плоскостей истинного меридиана наблюдателя и первого вертикала дает четыре главные линии на плоскости истинного горизонта наблюдателя, которые указывают на главные точки горизонта: N, S, Ost и W. Если наблюдатель станет лицом к северу, то за спиной у него будет юг, справа—восток, слева—запад. Линии N—S, Ost—W в любой точке земной поверхности (кроме полюсов) занимают вполне определенное положение. Направления N, S, Ost и W называют главными направлениями, или главными румбами, которые делят истинный горизонт на четыре четверти: NOst— северо-восточную, SOst — юго-восточную, SW—юго-западную и NW—северозападную. Каждая четверть делится на 8 румбов, а весь горизонт—на 32 румба.Основные географические точки, линии и круги на земном шаре.Земля непрерывно вращается в направлении с запада на восток. Диаметр, вокруг которого происходит это вращение, называется осью вращения Земли.Земля непрерывно вращается в направлении с запада на восток. Диаметр, вокруг которого происходит это вращение, называется осью вращения Земли.
Вертикальную плоскость, проходящую через глаз наблюдателя перпендикулярно плоскости истинного меридиана наблюдателя, называют плоскостью первого вертикала (плоскость 3). Она пересекается с плоскостью истинного горизонта наблюдателя по линии Ost—W. Таким образом, пересечение взаимно перпендикулярных плоскостей истинного меридиана наблюдателя и первого вертикала дает четыре главные линии на плоскости истинного горизонта наблюдателя, которые указывают на главные точки горизонта: N, S, Ost и W. Если наблюдатель станет лицом к северу, то за спиной у него будет юг, справа—восток, слева—запад. Линии N—S, Ost—W в любой точке земной поверхности (кроме полюсов) занимают вполне определенное положение. Направления N, S, Ost и W называют главными направлениями, или главными румбами, которые делят истинный горизонт на четыре четверти: NOst— северо-восточную, SOst — юго-восточную, SW—юго-западную и NW—северозападную. Каждая четверть делится на 8 румбов, а весь горизонт—на 32 румба.Основные географические точки, линии и круги на земном шаре.Земля непрерывно вращается в направлении с запада на восток. Диаметр, вокруг которого происходит это вращение, называется осью вращения Земли.Земля непрерывно вращается в направлении с запада на восток. Диаметр, вокруг которого происходит это вращение, называется осью вращения Земли.


