Изменение силы тяжести внутри Земли

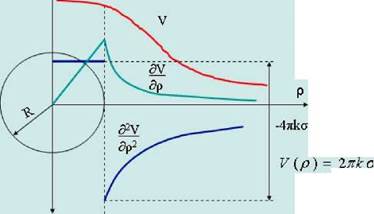
Если считать Землю однородным по плотности шаром, то потенциал внутри шара достигает максимума в его центре (рис. 2.4), плавно уменьшаясь при приближении к поверхности шара

и за его пределами. Сила притяжения — в центре шара равна нулю и с возрастанием ρ ее

др

значение увеличивается пропорционально расстоянию от центра шара до его поверхности. С удалением от центра потенциал и сила притяжения уменьшаются обратно пропорционально соответственно первой и второй степени расстояния. Т. е. потенциал притяжения однородного шара и его первые производные являются конечными и непрерывными функциями во всем пространстве.

Вторая производная на поверхности шара терпит разрыв и изменяется скачком на ±4πkσ (плюс при переходе из внутренней области во внешнюю, минус - при переходе извне вовнутрь). Соответственно, во внутренней области действует уравнение Пуассона, а во внешней - уравнение Лапласа (см. свойства потенциала). Таким образом, потенциал и все его производные вне притягивающих масс являются гармоническими функциями.

V ^V

Потенциал притяжения внутри однородного шара

ЪкМ\

V(p) =

2R

Масса сферы

ЪК'

М = -; 3

Тогда

>Л ² - — яка_гр² 3

Где <Т -средняя плотность сферы,

R -радиус сферы, р — расстояние от центра сферы до данной точки внутри нее

В последней формуле первый член - потенциал притяжения однородного шарового слоя, заключенного между сферами с радиусами р И R, а второй член -потенциал внутреннего шар ас радиусом р.

Рис. 2.4. Изменение потенциала и его производных для однородного шара.

В области притягивающих масс в некоторых точках или сам потенциал, или его производные теряют свою непрерывность (не гармонические). Эти точки называются особыми точками. Для потенциала и всех его производных особой точкой является центр, а для вторых производных - еще и поверхность тела. Но особые точки потенциала и его производных могут находиться не только внутри притягивающего тела, но и на его поверхности.

 

 

1200,	g, ran
		по Буллену
			по Булларду
1000 ■			^^—по Лежанщру^1
800 ■
GOO -	Граница,	ВДра \\\
400 ■
200 ■	\
о ■		H, км
	0 1000 2000 3000 4000 5000 6000

Рис. 2.5. Графики изменения силы тяжести внутри Земли по данным различных авторов.

На поверхности они совпадают с ее геометрическими особенностями - точками излома границ, угловыми точками. Зная положение особых точек, иногда можно определить геометрические параметры притягивающего тела.

Как показывают расчеты, реальную Землю нельзя считать однородным шаром. Зная среднее значение ускорения силы тяжести на поверхности Земли и ее радиус, можно рассчитать среднюю плотность Земли, которая равна 5,52 г/см³. Однако многочисленные измерения и расчеты показывают, что средняя плотность земной коры равна 2,8 г/см³, а для верхней мантии среднее значение плотности 3,3 г/см³. Это означает, что плотность внутри Земли меняется с глубиной. В зависимости от принятого закона изменения плотности с глубиной различные авторы получают разные графики (рис. 2.5) изменения силы тяжести с глубиной. Большинство исследователей придерживаются мнения, что на границе ядра Земли сила тяжести имеет небольшой максимум, а затем быстро уменьшается к центру.