Вторые производные потенциала силы тяжести и их физический смысл

Первые производные потенциала силы тяжести V по осям координат X, Y, Z:

dV dV dV — = Vx; — = Vy; — = Vz = g дх ду dz

(2.17)

определяют скорости изменения потенциала силы тяжести по направлениям этих осей и равны проекциям ускорения силы тяжести на эти же оси.

В гравиразведке используются и вторые производные потенциала силы тяжести, поэтому рассмотрим их физический смысл. Поскольку потенциал V является функцией трех переменных, он имеет шесть вторых производных.

д²У. cfV_. dV. д²У. д²У. д²У

дх^{2 ;} ду^{2 ;} dz^{2 ;} дхду ^; dxdz ^; dydz Для краткости обычно используется такая форма записи:

Vxx, Vyy, Vzz, Vxy, Vxz, Vyz. Физический смысл производных Vzx, Vzy, Vzz легко понять из выражений:

dxdz dx\dz) дх дх

dydz dyydzj dy dy

₌ Ц^В±УЛ ₌ % (2.20) dydj d d

g. (2.21) d

dzdz dzydz) dz dz

Эти производные иногда называют смешанными (вертикально-горизонтальными) Отсюда видно, что Vzx, Vzy, Vzz являются производными ускорения силы тяжести по осям координат и определяют скорости изменения g по направлениям этих осей.

Величина Vzs — VZX² + V_ZY² называется горизонтальным градиентом силы

dg тяжести: V_ZS = —, где s - направление максимального изменения силы тяжести в

ds

горизонтальной плоскости. Полная величина максимальной скорости изменения силы тяжести g в пространстве определяется из равенства

+ V +V О??}

где r - направление действия притягивающей силы.

Три другие вторые производные потенциала силы тяжести (горизонтальные) Vxx, Vyy, Vxy определяют форму уровенной поверхности в данной точке Р. Если через нормаль к уровенной поверхности (через ось Z) провести ряд плоскостей, то получим несколько так называемых нормальных сечений уровенной поверхности, каждое из которых будет плоской кривой (см. рис.2.3). Угол с одной из этих плоскостей и плоскостью XPZ обозначим φ. Из дифференциальной геометрии известно, что кривизна нормального сечения в данной точке:

— =---- (VXX cos²<p+Vxy sin2<p+VYY sin² ф)) p g

Для нормальных сечений, совпадающих с плоскостями XPZ и YPZ:

— = ~7_Ш — = ~Г„ (2-24)

Pxz g Pyz g

Пусть углом (рц определяется сечение с максимальной кривизной

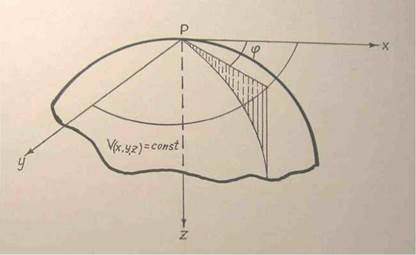
Рис. 2.3. Нормальные сечения уровенной поверхности.

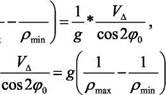Тогда разность кривизн будет определяться

( 1 1

где V_A=Vyy- У_ж. Величина R -

(2.25)

называется вектором разности

кривизн (или вектор кривизны) и характеризует уклонение данной уровенной поверхности от сферической, поскольку для сферы R = 0. Соответственно, величины R cos 2$>₀ = V_A и

R sin 2<р₀ = —IVxy называются составляющими вектора кривизны.

Таким образом, производные Vxx, Vyy, Vxy определяют разность кривизн главных нормальных сечений уровенной поверхности и азимуты этих сечений.

Основной единицей измерений вторых производных потенциала силы тяжести в системах СИ и СГС является 1/с², однако для практических расчетов чаще используют либо единицу Этвеш (Е), либо мгл/км. Соотношения между этими единицами следующие:

1 Е = 10-⁹ 1/с², 1 мгл/км = 10 Е.