
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы решения прямой задачи.Содержание книги
Поиск на нашем сайте В практике гравиразведочных работ обычно рудные тела аппроксимируются правильными телами: антиклинальные и синклинальные складки можно принять за горизонтальные цилиндры, дайки - за вертикальные пласты, изометричные залежи при глубине залегания центра, большей их радиуса - за сферы и т. д. Неправильные и сложные объекты могут аппроксимироваться набором правильных тел. Это удобно тем, что для правильных тел аналитические выражения поля силы тяжести и его градиентов известны. Например, выражения поля силы тяжести Ag и его градиентов VZX и VZZ для сферы имеют вид (при у=0): к'М'%\ (2-75) k-Mc.(2h2-x2). Z (x2 + h2f2 ' (2'76) 3k-Mc-h-x m ( л y (2'77) Для двухмерного горизонтального кругового цилиндра (т.е. бесконечного простирания в плоскости чертежа): 2к-т -h Vz=Ag= (х +h)
4к-тц-к-х — 7~2 — 7КГ- (2-80) ()xh222 где k - гравитационная постоянная, равная 6,67 *10"8 см3/г с2; Mс - избыточная масса сферы, определяемая как произведение ее объема на избыточную плотность (разность плотностей объекта и вмещающих пород); mц - избыточная масса единицы длины цилиндра, определяемая как произведение площади сечения цилиндра на избыточную плотность. х - текущая координата; h - глубина центра сферы или осевой линии цилиндра; Начало координат обычно выбирают в эпицентре тела. Анализ полей, вызванных правильными телами, дает возможность определить характерные точки кривых (экстремумы, точки перегиба, переход через ноль и др.) и по их положению оценить параметры искомого объекта. Для этого используются приемы, рассматривавшиеся ранее в курсе математического анализа. Например, для отыскания экстремумов необходимо взять производную функции по х и приравнять ее к нулю, при отыскании точек смены знака сама функция приравнивается к нулю и т.д. Вид графиков Vz, Vzx, Vzz над сферой и горизонтальным круговым цилиндром приведен на рис. 2.30 и 2.31.
X Рис. 2.30. Гравитационное поле сферы (шара)
Рис.2.31. Гравитационное поле кругового горизонтального цилиндра. Для горизонтального тонкого пласта, которым в первом приближении можно аппроксимировать нефтеперспективные структуры или залежи, аналитические выражения составляющих поля силы тяжести представлны на рис. 2.32. о ■*_ f» X + D. X - D н X ДН 2D Н - глубина верхней кромки пласта, 2D - ширина пласта, ДН - вертикальная мощность, m - линейная плотность m = ДстДН V7T = 2ктН\ --------------- =----- ____________ {X-D)2+H2
Vzz = 2km X + D
Рис. 2.32. Аналитические выражения поля силы тяжести над тонким горизонтальным пластом
Рис. 2.33. Графики составляющих поля силы тяжести над тонким горизонтальным пластом Графики Vz, Vzx, Vzz над тонким горизонтальным пластом показаны на рис. 2.33. Следует обратить внимание, как изменяются графики в зависимости от ширины пласта - на верхнем рисунке показаны графики при полуширине пласта, не превышающей глубину его осевой линии, а на нижнем - при полуширине, превышающей эту глубину.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.138 с.) |

 ()xh222
()xh222
 DY+H2 (X-DY+H1
DY+H2 (X-DY+H1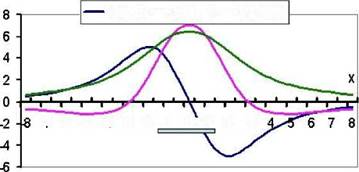
 -7 -6 -6
-7 -6 -6


