Различие и взаимосвязь гравитационных и магнитных аномалий

Особенности гравитационных и магнитных аномалий

Если обозначим V — гравитационный потенциал, U — магнитный потенциал, то для точки, лежащей вне притягивающей массы М при условии, что притягивающая масса -точка или сфера

V = k—. (3.28)

г

Если масса имеет произвольную форму, то потенциал во внешней точке определяется, как объемный интеграл

-a(x,y,z)-dx- dy-dz

(x²+y²+z²yi где k - гравитационная постоянная, σ(x,y,z) - функция плотности объекта, dx dy dz -

2 2 2 1

элемент объема, r = (x +y +z 2)² - расстояние от начала координат до центра элементарного объема. При этом справедливо уравнение Лапласа:

8²V 8²V 8²V „

или в другой записи Vxx + Vyy + Vzz = 0.

То есть гравитационное поле нацело определяется тем, как распределены массы внутри притягивающего объекта.

Магнитный потенциал определяется поверхностным и объемным интегралами следующим образом:

r/_ff Jcospdxdy rrr divJdxdydz _{d z}

• • •? 7 1, К J J J,? T 1. j/,

s (x +y +z ² г (x +y +z 2)²

где - угол между направлением намагниченности J объекта в данной точке его поверхности и нормалью к этой поверхности.

Обозначим J-cos<p = J_n = а. Эту величину называют поверхностной плотностью

,. _ J_x dJ_y dJ_z) _

намагничения. Величина divJ = — —- J---- y ч---- z = р называется объемной

\у дх ду dz J

намагниченностью, в которой J_M J_y,J_z - составляющие вектора намагниченности по осям координат. Поскольку r = (x² + y² + z²)1², dx dy = dS, а dxdy dz = dV, можно записать:

S V При однородном намагничивании J = const и div J = 0. Тогда: • cos cp ■ dS

(3.33)

"=fl-

s

Формула (3.33) означает, что при однородной намагниченности объекта магнитное поле определяется только тем, как распределены полюса по поверхности тела. При интерпретации мы не знаем закона распределения намагниченности внутри тела, поэтому всегда предполагается однородная намагниченность объекта. Если же мы знаем, что объект намагничен неоднородно, обычно разбиваем его на более мелкие тела, намагниченные однородно.

Формулами (3.29) и (3.32) определяются основные различия между гравитационными и магнитными аномалиями.

Связь же между гравитационными и магнитными аномалиями при однородной намагниченности объектов определяется уравнением Пуассона:

1 (_ dV _ dV _ dV),„„„

U =------- \J_X — + J_r — + J₇ —, (3.34)

ka у ox dy dz J

где U и V - соответственно магнитный и гравитационный потенциалы, σ- плотность объекта, J- его намагниченность с составляющими по осям Jx,Jy,Jz. Формулу (3.34) обычно приводят в более короткой записи

U = ~(J_ZV_Z+J_TV_T+J_ZV_Z). (3.35)

ka

При вертикальной намагниченности JX = Jy ⁼ 0, JZ = J и формулу (3.35) можно записать таким образом:

U = ~Vz, (3.36)

ka

то есть ускорение силы тяжести пропорционально магнитному потенциалу. Если продифференцировать левую и правую части уравнения (3.35) по направлениям x, y, z, получим:

^ х ⁼~₇ k

U у =^-(J_xV_xr+J_rV_rr+J_zV_zr) (3.37)

ka

UZ ⁼~₇ ka

где U_X = X, UY =Y, U_Z = Z - соответственно северная, восточная горизонтальные и вертикальная составляющие (проекции) полного вектора магнитной индукции.

Для двухмерных объектов Jy = 0, поэтому:

ко

Y = ^-(J_XV_XY+J_ZV_ZY) (3.38)

ко

Z = -^(J_XV_XZ+J_ZV_ZZ) ко

При вертикальной намагниченности объектов (с чем чаще всего приходится сталкиваться при интерпретации) J_X = Jy = 0, JZ = J. Тогда:

ко

Y = ^-V_zr (3.39)

ко

z =—v_zz

ко ^ZZ А если профиль направлен в плоскости намагничения двухмерного объекта, то

H = JV_ZY

Irrr

^Ка (3.40)

Z-— V

^ ~ _V ' ZZ

ко

Формулы (3.39) - (3.40) означают, что из составляющих магнитного поля X,Y,Z при определенных условиях можно получить соответствующие производные ускорения силы тяжести Vzx, Vzy, Vzz и способы интерпретации графиков этих составляющих будут аналогичны.

Таким образом, можно сформулировать различия между гравитационными и магнитными аномалиями.

1. Величина гравитационного потенциала и силы притяжения - функции
объемного распределения масс, а магнитный потенциал и напряженность для
однородно намагниченных тел можно рассматривать как функцию
поверхностного распределения магнитных полюсов или как функции
непрерывного объемного распределения намагниченности внутри тел.

2. Магнитные массы полюса расположены попарно, поэтому всегда есть силы
притяжения и отталкивания.

3. Напряженность магнитного поля теоретически никогда не бывает направлена в
центр тела, а всегда по касательной к силовым линиям. Полная напряженность
гравитационного поля теоретически всегда направлена в центр тяжести тела.

4. График поля силы тяжести Vz при симметричном объекте всегда симметричен
относительно его эпицентра и наоборот - при несимметричном объекте график
несимметричен. График вертикальной составляющей вектора магнитной
индукции Z может быть несимметричным относительно центра объекта при
симметричности объекта и наоборот - при несимметричном объекте графики
могут симметричны в зависимости от направления намагниченности объекта,
т. е. расположения полюсов по его поверхности.

5. Напряженность гравитационного поля изменяется обратно пропорционально
квадрату расстояния до источника, а напряженность магнитного поля -
обратно пропорционально кубу этого расстояния, поэтому магнитные
аномалии по сравнению с гравитационными более чувствительны к неглубоко
залегающим объектам.

6. При вертикальной намагниченности объектов аномалии Vz (Ag)
пропорциональны аномалиям магнитного потенциала. Все способы
интерпретации аномалий Z можно применять для интерпретации аномалий Vzz
и наоборот.

Исходя из перечисленных особенностей магнитных аномалий форма магнитных аномалий Н, Z и ΔТ зависит не только от формы аномалиеобразующего объекта, но и от направления его намагниченности. Если при симметричном объекте аномалии гравитационного поля Vz и Vzz всегда также симметричны, то магнитные аномалии Z и ΔТ могут быть несимметричны при симметричном объекте и, наоборот, могут быть симметричны при несимметричном объекте. Например, формулы для расчета вертикальной (Z) и горизонтальной (Н) составляющих полного вектора магнитной индукции (Т) над круговым горизонтальным цилиндром имеют вид, показанный на рис. 3.21. На рис. 3.22 - 3.24 показан вид графиков Z и Н над круговым горизонтальным цилиндром, намагниченным в разных направлениях. Следует обратить внимание на то, что при вертикальном намагничении совпадают графики Z и ΔТ, а при горизонтальном намагничении совпадают графики Н и ΔТ. При наклонном же намагничении все графики не совпадают. Надо иметь в виду, что Т и ΔТ - это не одно и то же. Для наших широт при вертикальном намагничении можно считать, что Z = ΔТ, что видно и из приведенных графиков.

z_N = ъм

(к² - х²)cos у - Ihx ■ sin

 

h_n = -гм

(h² - x² Jsin у + 2hx ■ cos у

Пересчет из вертикального в наклонное намагничение

Z_N = Z_vcosy-H_vsiny H_N = Z_vsiny + H_vcosy

Справедливо и обратное - пересчет из наклонного в вертикальное намагничение

Z_v = Z_N cosy - H_N siny

H_v = Z_N siny + H_N cosy

Рис. 3.21. Вид формул ZиН для расчета магнитных полей горизонтального кругового цилиндра

Магнитное поле кругового горизонтального цилиндра

Z, нТл —i—Н.нТл— РТ.нТл

800: -700:.660 ■ -500 -400 -300 -200 -100 0\ 100 200 300 400 500 600 700 - 800

 

Рис. 3.22. Графики Z,НиΔТ для кругового горизонтального цилиндра при вертикальном намагничении. Совпадают графики Z, и ΔТ.

Магнитное поле кругового горизонтального цилиндра

Z, нТл—|— ЦнТл —«ЕТГ.нТл

X, м

800-700 -600 -50Q -400 -300 -200 1° = 60°

 

Рис. 3.23. Графики Z,НиΔТ для кругового горизонтального цилиндра при наклонном намагничении под углом 60°.

в

Магнитное поле кругового горизонтального цилиндра

Z. нТл —i—Н.нТл —ч—DT.Hln

800 -700 -BOO -500 -400 -300 -200 -100

 

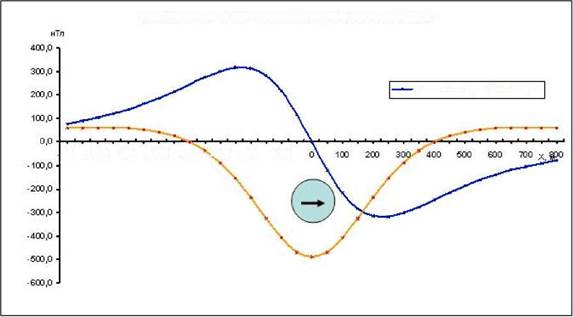
Рис. 3.24. Графики Z,НиΔТ для кругового горизонтального цилиндра при горизонтальном намагничении. Совпадают графики Н и ΔТ.

Практическое задание № 6

• Проанализировать формулы Z, H, T для вертикально намагниченного кругового
горизонтального цилиндра. Определить зависимости, связывающие абсциссы
характерных точек графиков с глубиной залегания цилиндра.

• Рассчитать и построить графики Z, H, T для цилиндра, проверить положение
характерных точек графиков и проанализировать изменения графиков при изменении
направления намагничения цилиндра.

• Считая, что известны только графики и намагниченности цилиндра и вмещающих
пород, определить минимальную глубину задания заверочной скважины.

• Сделать выводы, как изменяются графики в зависимости от изменения направления
намагниченности