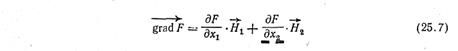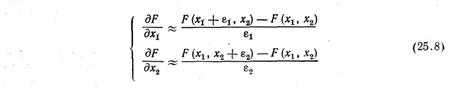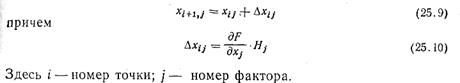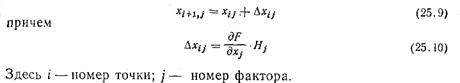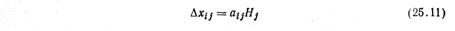Метод покоординатного спуска.

Этот метод сводится к следующему. Выбираются координаты начальной точки поиска x_1н и x_2н, т.е. те значения х₁и х₂, от которых мы начнем искать оптимум. Выби­раются единичные приращения обоих факторов (шаги) Н₁ и Н₂, а также малые приращения факторов e₁ и е₂. Выбор всех этих величин определяется физическим смыслом задачи и той инфор­мацией о ней, которой мы располагаем заранее.

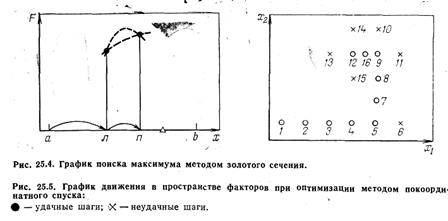
Рассчитывается значение R(х₁,х₂) в точке 1 (рис. 25.5). Далее, не меняя величины х₂, начинаем двигаться вдоль оси х₁, давая на каждом шаге этому фактору приращение Н₁ (или - Н₁, в зависимости от того, при движении в какую сторону будет наблюдаться рост R). На каждом шаге — в точках 2, 3, 4 и т. д. — проводится расчет R. Шаги продолжаются до тех пор, пока продолжается рост R. Неудачными будем считать те шаги, на которых получено меньшее значение R, чем на предыдущих; на рисунке они обозначены крестиками. После первого неудачного шага (точка 6) возвращаемся в предыдущую точку (в данном случае — в точку 5), фиксируем величину х₁и начинаем изменять х₂, давая ему приращения Н₂ или - Н₂ (точки 7, 8, 9, 10). Затем снова движемся вдоль оси х₁(точки 11, 12, 13), снова меняем направление (точки 14, 15) и т. д. Если факторов больше двух, то после движения вдоль осей х₁и х₂проводится движение вдоль осей х₃, х₄ и т.д. до последней, и лишь затем вновь движем­ся вдоль оси х₁.

На рис. 25.5 изображена ситуация, когда из точки 12 двигаться некуда: во всех окружающих точках (9, 13, 14, 15) значение R меньше, чем в данной. Это зна­чит, что максимум находится недалеко от точки 12 и прежние крупные шаги из токи 12 переносят через него. В этом случае шаги уменьшают, вдвое (см. точку 16) и продолжают поиск уменьшенными шагами. Уменьшение шага может производиться неоднократно. Но в тот момент, когда уменьшенные шаги оказы­ваются меньше, чем соответственно e₁ и е₂, логично считать, что максимум зафиксирован достаточно точно и можно закончить расчет, приняв лучшую точку за оптимум.

 

Метод градиента

Как и в методе покоординатного спуска, вначале выберем ко­ординаты исходной точки х₁и х₂, шаги Н₁ и Н₂ и малые прира­щения e₁ и е₂. Движение к оптимуму начнем не вдоль какой-либо оси координат, а в направлении градиента целевой функции (или, если ищем минимум, то в противоположном градиенту направлении). Поскольку Н₁ и Н₂ приняты за единич­ные приращения координат, формула градиента получит вид:

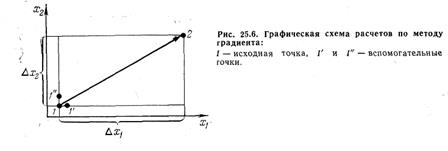
Ясно, что для расчета направления градиента необходимо знать частные производные целевой функции по факторам. Для расчета производных проводится вспомогательная серия расчетов (рис. 25.6).

Около начальной точки 1 ставятся две вспомогательные точ­ки: 1’на расстоянии e₁ вдоль оси х₁и 1’’ на расстоянии е₂ вдоль оси х_2, и в них рассчитывается R. Производные находят по фор­мулам:

После этого делают шаг в точку 2 для следующего расчета R. Ее координаты находятся по формуле

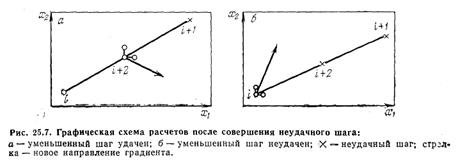
Дальше можно поступать по-разному. Можно определить про­изводные в новой точке i+1, найти направление градиента, сде­лать шаг и т. д. Но чаще делают иначе. Если шаг оказался удач­ным, т. е. если R_i+1>R_i (при поиске максимума), то делают следующий шаг в том же направлении, подставляя в формулу (25.10) ранее найденные значения производных. Практически наверняка это будет уже не направление градиента: направление градиента в разных точках пространства факторов — разное, если только функция R не является линейной. Но можно надеяться, что еще один шаг в прежнем направлении снова даст приращение R нужного знака, хотя и не максимально возможное (так как от градиента мы отклонились); зато мы сэкономили на том, что не надо лишний раз считать производные. Если и этот шаг удачен, шагнем еще раз и т. д.

В случае, когда шаг неудачен, вероятно, поверхность настолько искривлена, что данное направление перестало вести вверх, мы «перескочили» через ту окрест­ность предыдущей точки, в которой функция возрастала. Поэтому в таком случае обычно уменьшают шаг, например, вдвое. Теперь, если уменьшенный шаг в том же направлении будет удачен, нет смысла делать еще шаг, поскольку он приведет в «плохую» точку (см. рис. 25.7, а: крестик — неудачный шаг, (i+2)-точка по­ловинного шага). В этом случае около точки (i+2) поставим вспомогательные точки для расчета производных по формуле (25.8), найдем новое направление градиента и двинемся по нему (на рис. 25.7 вспомогательные точки - кружки, новое направление градиента — стрелка). Если же и уменьшенный шаг не приведет в «хорошую» точку (рис. 25.7,6), то вернемся в точку i и будем в ней искать направление градиента.

 

Движение продолжают до тех пор, пока шаги не станут очень малыми. Уменьшение шагов объясняется двумя причинами. Во-первых, неоднократным уменьшением в тех случаях, когда большой шаг оказывался неудачным. Во-вторых (это принципиально важ­нее), тем, что вблизи оптимума производные близки к нулю, и фор­мула (25.10) дает уже очень малые приращения.

Для останова вычислений можно использовать момент, когда оба приращения Dx_ij окажутся меньше, чем соответствующие ма­лые величины е_j.

 

Метод случайного поиска

В методе покоординатного спуска движение из точки производится шага­ми, направленными вдоль одной из осей координат. В методе градиента - шагами по направлению градиента. В случайном поиске шаг из данной точки осуществляется в случайном направлении.

При двух факторах в принципе можно поступить так. Нанести на график оси координат х₁ и х₂ и начальную точку (рис. 25.8). Затем бросить в график кусочек графита, целясь в точку 1. Линия, соединяющая точку 1 с точкой по­падания 2, и определит случайное направление.

Разумеется, практически случайное направление находят по-иному. Пользуясь формулой (25.9),

но Dx_ij находят не по формуле (25.10), а по соотношению

где а_ij — случайное число, которое обычно либо находят по таблицам случайных чисел, имеющимся в большинстве книг и справочников по теории вероятностей, математической статистике и теории эксперимента, либо рассчитывают на ЭВМ по специальным программам (генераторы случайных чисел).

Если шаг оказался удачным, обычно продолжают движение в том же направлении; если неудачным — рассчитывают новое слу­чайное направление.

Практика оптимизации показывает, что в ряде случаев (мно­го факторов, очень сложный вид поверхности, влияние ограни­чений) случайный поиск может оказаться эффективнее остальных методов.