Аналитический метод оптимизации

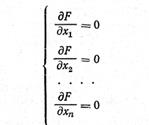
Применяют к задачам, для которых целевая функция выражена аналитически и дифференцируема во всем диапазоне исследования. Экстремум находится из условия равенства нулю производных функции.

Пусть целевая функция задана формулой R=f(u₁, u₂,…u_n). Классический метод отыскания экстремума заключается в решении системы

Левые части уравнений (24.1) — функции от факторов u₁, u₂,…u_n. Поэтому решение системы может дать величины u_1опт, u_2опт,…u_nопт, являющиеся оптимальными значениями факторов; их совокупность определяет оптимальное решение задачи. Если оптимизируется технологический процесс, то этому решению соответствует оптимальный режим.

Однако в том, что полученные значения действительно оптимальны, нужно убедиться. Необходимо выяснить четыре обстоятельства.

1. Действительно ли решение системы (24.1) определяет экстремум: известно, что условию (24.1) может удовлетворять и седловая точка или точка перегиба.

2. Получен ли экстремум нужного знака (максимум, если нас интересует максимум, или минимум в обратном случае).

3. Если система имеет несколько решений, то какое из них отвечает глобальному оптимуму, а какие — локальным. Так, если зависимость имеет несколько максимумов, то глобальным будет тот из них, который выше всех остальных; остальные будут локальными.

4. Все ли ограничения соблюдаются в точке экстремума.

 

Оптимизация простой реакции

рассмотрим реакцию вида:

Наши рассуждения будут верны практически для любой обратимой (и необратимой) реакции.

Если химическая реакция проходит без побочных стадий, то удается найти очень простой критерий оптимальности — скорость реакции.

Согласно схеме, данной в предыдущем разделе, теперь нужно установить ограничения и выбрать оптимизирующие факторы. Но часто бывает удобно сначала записать целевую функцию, а уже потом перейти к ограничениям и оптимизирующим факторам.

Целевая функция имеет вид

Таким образом, наш критерий зависит от трех параметров: температуры Т и концентраций C_а и C_в. По-видимому, эти три величины можно было бы избрать в качестве оптимизирующих факторов. Но необходимо учесть, что концентрации C_A и C_B не относятся ко входам рассматриваемой системы. Они сами получаются как результат реакции. Ясно, что для увеличения скорости следовало бы иметь как можно большее значение c_а и как можно меньшее c_b. Цель же процесса — противоположная: увеличить c_b и уменьшить с_а. Поэтому концентрации нельзя рассматривать как независимые факторы.

Итак, есть лишь один независимый фактор, которым можно влиять на R - температура. Рассматриваемая задача обычно называется задачей об оптимальной температуре химической реакции.

Но при разных концентрациях влияние температуры может быть различным. Поэтому будем решать задачу в такой постановке. Фиксируем некоторые значения C_A и C_B и при этих значениях найдем оптимальную температуру. Это означает, что концентрации веществ А и В выступают в нашей задаче как ограничения типа равенства.

Кроме того, учтем одно ограничение типа неравенства, которое существует в любой практической задаче: температура не может превысить некоторого максимального значения Т _макс

Прежде, чем обращаться к формуле (24.1), рассмотрим два случая, когда оптимум можно найти из физических соображений, без расчета.

Если реакция необратима, т. е. k ₀₂ = 0, то в правой части формулы (24.2) остается только первый член, который с ростом температуры растет неограниченно. Максимум в смысле условия (24.1) отсутствует. Тогда оптимум определяется ограничением: следует поддерживать максимально допустимую температуру

Пример 24.1. Оптимальная температура необратимой реакции.

Реакция сгорания топлива практически необратима. В тех случаях, когда требуется максимальная интенсивность горения, следует поддерживать максимально достижимую температуру. На увеличение этой температуры направлены усилия при конструировании современных топок.

Если реакция обратима, но эндотермична, т. е. E₁>E₂, то результат рассуждений — тот же, что и в предыдущем случае. Действительно, с ростом температуры и равновесие сдвигается вправо, и скорость прямой реакции растет. Поэтому оптимум определяется формулой (24.4).

Пример 24.2. Оптимальная температура эндотермической реакции. К рассматриваемому типу относится реакция

Открытая еще в XV{II веке Г. Кавендишем, она нашла практическое применение лишь в начале нашего века, когда дешевая гидроэлектроэнергия и разработка дуговых печей позволили поднять Т_ытс до 3000 К. Но в дальнейшем этот метод фиксации азота был вытеснен синтезом аммиака. Ныне прямое окисление азота вновь обретает перспективы, что связано с повышением уровня ограничения: после появления плазмотронов можно рассчитывать на увеличение его конкурентоспособности.

Если реакция — обратимая экзотермическая, т. е. E₁<E₂, то к решению потребуется применить иной подход. В этом случае с ростом температуры вначале более существенным будет возрастание скорости прямой реакции: обратная еще слишком медленна. При дальнейшем повышении температуры обратная реакция, имеющая большую энергию активации, начинает «нагонять» прямую. При данном составе существует температура Т_равн, при которой смесь находится в равновесии, r = 0; затем ход реакции смещается влево.

Где-то посередине имеется температура, при которой суммарная скорость реакции максимальна. Это и есть Т_ОПТ.

Для ее расчета запишем условие (24.1) для формулы (24.2):

Здесь записана частная производная по Т, поскольку она берется при фиксированных С_А и C_B.

Из уравнения (24.5) несложными преобразованиями можно получить формулу оптимальной температуры

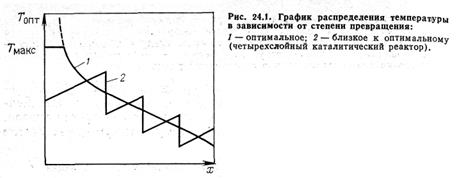
Из уравнения (24.6) следует, что чем выше C_A и чем меньше C_B, тем выше Т_ОПТ; по мере роста степени превращения величина Т_ОПТ, уменьшается. При C_B →0 по формуле
Т_ОПТ →∞. Поэтому на начальном участке реактора следует устанавливать максимально допустимую температуру Т_макс, а с момента, когда определенная по уравнению (24.6) Т_опт сравнивается с Т_макс, изменение температуры должно определяться этим уравнением. Это положение иллюстрирует кривая 1на рис. 24.1, изображающая оптимальный ход температуры в зависимости от степени превращения.

Реально осуществить такое распределение температуры чрезвычайно трудно, поэтому применяют другие распределения, более или менее приближающиеся к оптимальному. Так, ломаная 2 на рис. 24,1 показывает ход температуры в пятислойном каталитическом реакторе, в каждом слое которого реагирующая смесь адиабатически разогревается за счет тепла реакции, а между слоями охлаждается в теплообменнике. Такое распределение температур приведет к несколько худшим результатам (большему объему катализатора), но его сравнительно легко осуществить. Чем больше ступеней катализа, тем ближе ломаная к оптимальной кривой. Если реакцию проводят в аппарате смешения, то во всем его объеме имеем одну и ту же степень превращения. Ей соответствует одна точка на кривой 1 (рис. 24.1), соответствующая оптимальной температуре для данного аппарата.