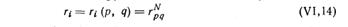Решение комбинаторной задачи

Наиболее наглядно метод динамического программирования можно демонстрировать при решении комбинаторной задачи, которую можно представить как многостадийный процесс принятия решений, т. е. выбор управления на каждой стадии из некоторого дискретного и конечного набора возможных управлений (решений).

Предположим, что существует N-стадийный процесс, на каждой стадии которого возможны п фиксированных состояний, и пусть из каждого состояния (i- 1)-й стадии процесса можно попасть в любое из п состояний следующей i-й стадии. На рис. VI-2 показано схематическое изображение двух стадий указанного процесса для случая n = 3.

Результат перехода из p-го состояния (i- 1)-й стадии в q-e состояние i-й стадии оценивается величиной r_i, которая может считаться функцией целых чисел р и q, т. е.

Задача состоит в выборе такой последовательности решений на каждой стадии, т. е. последовательности чисел

характеризующих переход с (i — 1)-й стадии в определенное состояние следующей i-й стадии, чтобы суммарное значение результата

имело максимальное значение.

Примем, что исходное состояние процесса задано. Тогда переход из него в любое из п возможных состояний 1-й стадии связан с возможностью выбора одного из п вариантов перехода. Число возможных вариантов перехода из исходного состояния на вторую стадию будет равно уже n², и, наконец, для всего N-стадийного процесса число возможных вариантов перехода из исходного состояния на N-ю стадию составит n^N.

Например, для n=3 и N= 10, т. е. для процесса, включающего 10 стадий, на каждой из которых возможны 3 состояния, величина n^N = 3¹⁰. Если оптимальное решение определяется методом прямого перебора всех возможных вариантов и для оценки каждого варианта требуется 1 сек, то для решения задачи нужно 3¹⁰ сек = 16 ч. Если же число стадий в процессе в 2 раза больше, т. е. N = 20, то время, необходимое для решения задачи этим методом, составит величину, примерно равную 960 тыс. ч (!).

Таким образом, метод прямого перебора в случае решения комбинаторных задач даже при использовании современных ЭВМ имеет весьма ограниченную область применения, поскольку возрастание числа вариантов, подлежащих проверке, при увеличении числа стадий и возможных на них состояний может очень быстро превысить возможности любой вычислительной машины.

Рассмотрим теперь, каким образом можно решить сформулированную выше комбинаторную задачу, используя метод динамического программирования. Как отмечалось выше, процедура решения задачи оптимизации при помощи принципа оптимальности начинается с оптимизации последней стадии процесса, результатом чего является набор оптимальных решений (управлений) на ней для любых возможных состояний входа этой стадии.

В данном случае оптимизация сводится к оценке возможных вариантов перехода из п состояний предыдущей (N- 1)-й стадии в п состояний последней N-й стадии. Таким образом, обследованию подлежат n² вариантов, что позволяет выделить п оптимальных управлений на этой стадии, соответствующих п состояниям предыдущей стадии и обеспечивающих переход на последнюю стадию с максимальными значениями результатов перехода r_N (p, q). Указанные значения, естественно, зависят от состояния предыдущей стадии, откуда осуществляется переход.

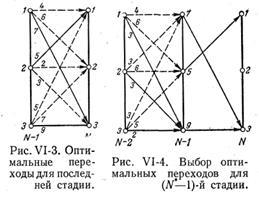
На рис. VI-3 оптимальные переходы выделены сплошными линиями. Числа у стрелок, выражающих возможные переходы, характеризуют оценку перехода. В обозначениях (VI, 15) решение задачи оптимизации последней стадии процесса запишется в виде:

где q^(j)_i - величина, показывающая, в какое состояние i-й стадии следует перейти из j-го состояния предыдущей стадии, чтобы получить максимальное значение результата перехода.

Подчеркнем еще раз, что управления, найденные на последней стадии, оптимальны для любой стратегии управления, которая принята на предыдущих стадиях процесса, поскольку обследованы все возможные состояния входа N-й стадии [выхода (N- 1)-й стадии].

Теперь можно определить оптимальное управление на предпоследней стадии при любом состоянии выхода (N- 2)-й стадии. На рис. VI-4 при изображении последней стадии оставлены только оптимальные переходы, дающие максимальный результат.

Выбор оптимального управления на (N- 1)-й стадии должен производиться с учетом уже найденного оптимального управления для последней стадии. Он потребует обследования также n² вариантов перехода на (N- 1)-ю стадию, так как переходы на N-ю стадию уже определены единственным образом. На рис. VI-4 оптимальные переходы на (N- 1)-ю стадию показаны сплошными линиями. В обозначениях (VI, 15) можно записать:

Интересно отметить, что найденные оптимальные переходы с учетом изолированной (N- 1)-й стадии совсем не оптимальны, так как в ее пределах существуют локальные переходы с большими значениями результатов.

Кроме того, оказывается, что конечное состояние на последней стадии уже определено однозначно, поскольку осталось только одно состояние (3) данной стадии, куда возможен переход с (N- 2)-й стадии с максимальным значением результата перехода, оцениваемым по двум последним стадиям.

После того как найдена оптимальная стратегия управления для двух последних стадий, можно перейти к выбору оптимального управления для (- 2)-й стадии (рис. VI-5), на которой обследованию подлежат также n² вариантов перехода, и т. д.

Продолжая изложенную процедуру, можно дойти до совокупности состояний на первой стадии процесса (рис. VI-6). Если исходное состояние процесса зафиксировано, как изображено на рис. VI-6, то на этой стадии выбор управления сведется к оценке п возможных переходов, для каждого из которых найдено значение результата перехода в конечное состояние процесса R^(j)_N (j = 1,..., n). Выбор перехода для первой стадии, соответствующего максимальному значению R^(j)_N, определяет номер j_опт. варианта перехода из исходного состояния в конечное и, следовательно, оптимальные управления на всех стадиях, которые можно теперь найти при просмотре маршрута с номером j_опт. от первой стадии до последней. На рис. VI-6 показан оптимальный переход при j=2.

Если же исходное состояние не определено и может быть выбрано из совокупности п исходных состояний, то на первой стадии также необходимо исследовать п² вариантов перехода (рис. VI-7), в результате чего можно найти одно (или несколько) исходное состояние, отвечающее максимальному значению результата для многостадийного процесса в целом.

Таким образом, сформулированная выше комбинаторная задача решена до конца. В процессе решения потребовалось исследовать всего Nn² вариантов, тогда как при применении метода прямого перебора нужно оценить n^N различных вариантов. Время решения комбинаторной задачи n=3 и N=20 при оценке одного варианта за 1 сек с использованием принципа оптимальности будет равно 20*3² = 180 сек= 3 мин, что в сравнении с 3²⁰ сек = 960 тыс. ч, необходимыми для решения задачи прямым перебором, позволяет весьма ощутимо представить преимущества динамического программирования при решении подобных задач.