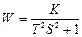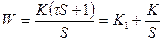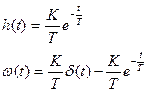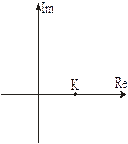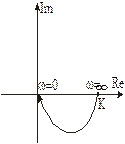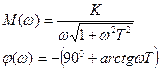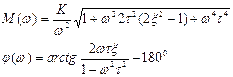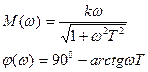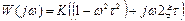Разновидность типовых звеньев САР

 

Типовым динамическим звеном САР является составная часть системы, которая описывается дифференциальным уравнением не выше второго порядка.

Звено, как правило, имеет один вход и один выход. По динамическим свойствам типовые звенья делятся на следующие разновидности: позиционные, дифференцирующие и интегрирующие. Позиционными звеньями являются такие звенья, у которых в установившемся режиме наблюдается линейная зависимость между входными и выходными сигналами. При постоянном уровне входного сигнала сигнал на выходе также стремится к постоянному значению.

Дифференцирующими являются такие звенья, у которых в установившемся режиме выходной сигнал пропорционален производной по времени от входного сигнала. Интегрирующими являются такие звенья, у которых выходной сигнал пропорционален интегралу по времени от входного сигнала.

Звено считается заданным и определенным, если известна его передаточная функция или дифференциальное уравнение. Кроме того, звенья имеют временные и частотные характеристики.

Передаточную функцию любой САР в общем случае можно представить как произведение передаточных функций следующего вида:

 

 

где K, n, T, x, t - постоянные величины, причём

 

K>0, n>0, T>0, 0<x<1, t>0

 

Эти передаточные функции определяют типовые динамические звенья. Передаточные функции и временные характеристики типовых звеньев приведены в таблице 3.2.

 

Таблица 3.2 Временные характеристики типовых звеньев

Тип звена	Передаточные функции	Временные функции
Позиционные звенья
Усилительное	W=K	h(t)=K×1(t) w(t)=K×d(t)
Апериодическое 1-го порядка
Апериодическое 2-го порядка Т1³ 2Т2	,
Колебательное 0<x<1
Консервативное

 

Тип звена	Передаточные функции	Временные функции
Интегрирующие звенья
Интегрирующее идеальное		h(t)=k×t w(t)=k×1(t)
Интегрирующее инерционное
Изодромное 1-го порядка
Изодромное 2-го порядка
Дифференцирующие звенья
Идеальное дифференциру-ющее	W=KS
Дифференциру-ющее инерционное
Форсирующее 1-го порядка

 

Частотные характеристики типовых звеньев приведены в таблице 3.3

Таблица 3.3 Частотные характеристики звеньев

Частотная передаточная функция	Амплитудная M(w) и фазовая j(w) характеристики	Амплитудно-фазовая частотная характеристика
W(jw)=K	M(w)=0 j(w)=0
Частотная передаточная функция	Амплитудная M(w) и фазовая j(w) характеристики	Амплитудно-фазовая частотная характеристика
Частотная передаточная функция	Амплитудная M(w) и фазовая j(w) характеристики	Амплитудно-фазовая частотная характеристика
Частотная передаточная функция	Амплитудная M(w) и фазовая j(w) характеристики	Амплитудно-фазовая частотная характеристика

 

В табл. 3.2 и 3.3 указаны лишь характеристики основных типовых звеньев. Кроме того существуют интегро-дифференцирующие звенья и неминимально-фазовые звенья. Интегро-дифференцирующие звенья имеют передаточные функции вида:

 

Где k-постоянный коэффициент

R(S) и Q(S)- полиномы от S первого или второго порядков.

К неминимально-фазовым звеньям относятся неустойчивые звенья, передаточные функции которые имеют хотя 6ы один положительный полюс. Неминимально-фазовыми являются также звенья, которые имеют бесконечное число полюсов в левой части комплексной плоскости. Эти звенья известны под названием звенья чистого запаздывания.

 

УСТОЙЧИВОСТЬ И КАЧЕСТВО САР