
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые соединения lti-моделейСодержание книги
Поиск на нашем сайте
Системы автоматического управления, как известно, часто задаются в виде структурных схем, которые представляют собой графическое изображение математической модели САУ в виде соединений элементарных динамических звеньев с ПФ низкого порядка. Если в системе отсутствуют перекрестные связи, то за счет выделения и преобразования так называемых типовых соединений звеньев всегда можно получить единую математическую lti -модель САУ. В теории управления к типовым относят три элементарных соединения динамических звеньев: параллельное, последовательное и встречно-параллельное. Для определения результирующей математической модели таких соединений в Control System Toolbox предусмотрены специальные функции и операции. В качестве lti -объектов могут использоваться все типы моделей. Однако, модели, входящие в типовые соединения, должны быть либо непрерывными, либо дискретными с одинаковым периодом квантования Ts. При этом тип результирующей модели определяется правилами предпочтения, согласно которым наивысший приоритет имеет s s-подкласс, затем следует подкласс zpk и далее объекты tf -подкласса. Поэтому результатом операции преобразования двух lti -объектов будет: · ss -объект, если хотя бы один из операндов относится к ss-подклассу; · zpk -объект, если операнды не относятся к ss -подклассу и хотя бы один из операндов является zpk -моделью; · tf -объект, если оба операнда принадлежат подклассу tf. Согласно этим правилам предпочтения в пакете Control System Toolbox перед выполнением операций все операнды более низкого приоритета переводятся в lti -модель операнда с наивысшим приоритетом. Если необходимо получить результирующую модель определенного подкласса, можно предложить два пути: после выполнения операции перевести результат в требуемый подкласс, либо преобразовать в этот подкласс все операнды до выполнения операции. Структура параллельного соединения двух моделей представлена на рис.1.1.
Рис. 1.1. Схема параллельного соединения
Для получения результирующей lti -модели sys при суммировании выходов можно использовать операцию сложения или эквивалентные ей функции parallel и plus, а при вычитании – minus:
sys = sys1 + sys2 sys = plus(sys1, sys2) sys = parallel(sys1, sys2) sys = sys1 - sys2 sys = minus(sys1, sys2)
Пример 1.20. Определение результирующей модели для параллельного соединения моделей с передаточными функциями
>> v1=tf(10, [1, 1]); >> v2=zpk([], [0, -2], 0.2); >> w20=v1+v2 Zero/pole/gain:
s (s+2) (s+1) Задание 1.20. Сформируйте с помощью функции parallel результирующую tf-модель h20 для параллельного соединения звеньев с ПФ:
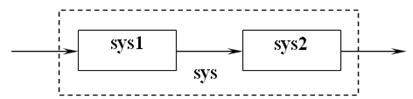
Схема последовательного соединения двух lti -моделей приведена на рис.1.2.
Рис.1.2. Схема последовательного соединения
Для определения результирующей модели sys можно использовать операцию умножения моделей sys1 и sys2 или две специальные функции series и mtimes:
sys = sys1 * sys2 sys = series (sys1, sys2) sys = mtimes (sys1, sys2)
Пример 1.21. Получение результирующей модели для последовательного соединения объектов с передаточными функциями V1(s) и V2(s).
>> w21=series(v1,v2)
Zero/pole/gain:
s (s+1) (s+2)
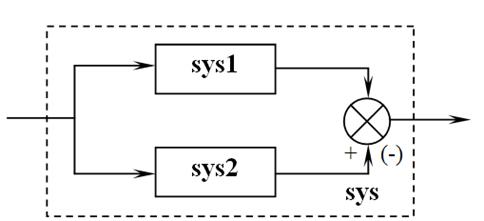
Задание 1.21. Сформируйте с помощью функции mtimes результирующую zpk-модель h21 для последовательного соединения звеньев с ПФ G1(s) и G2(s). Встречно-параллельное соединение моделей представлено на рис.1.3. В общем случае обратная связь может быть как отрицательной, так и положительной. Для получения результирующей модели этого соединения используется функция feedback, которая для отрицательной обратной связи может применяться в двух вариантах:
sys = feedback (sys1, sys2) sys = feedback (sys1, sys2, -1),
а при положительной обратной связи вызывается в следующем виде:
sys = feedback (sys1, sys2, 1),
где sys1 – охватываемая модель, sys2 – модель цепи обратной связи.
Рис. 1.3. Схема встречно-параллельного соединения
Пример 1.22. Определение результирующей модели для встречно-параллельного соединения звеньев V1(s) и V2(s).
>> w22=feedback(v1,v2)
Zero/pole/gain:
(s+2.521) (s^2 + 0.4786s + 0.7932)
Следует отметить, что в знаменателе полученной zpk -модели имеется оператор второго порядка. Это форма используется в MatLab при появлении в модели комплексно-сопряженных корней.
Задание 1.22. Сформируйте результирующую ss-модель h22 для схемы с отрицательной обратной связью, в которой sys1=G1(s), sys2=G2(s).
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.114.163 (0.009 с.) |

 ,
,  .
. 10 (s+2.01) (s+0.00995)
10 (s+2.01) (s+0.00995) ,
, 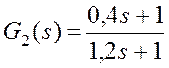 .
.
 2
2
 10 s (s+2)
10 s (s+2)


