
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет контура регулирования напряженияСодержание книги
Поиск на нашем сайте
Структурная схема первого внутреннего контура представлена на рис. 5.6. Здесь
Рис. 5.6. Структурная схема контура регулирования напряжения
В соответствии с методикой подчиненного регулирования координат внутренние контуры настраиваются по быстродействию на так называемый модульный оптимум, которому соответствует желаемая ПФ разомкнутой системы следующего вида
где В качестве
т.е. представляет собой колебательное звено с незначительным коэффициентом демпфирования Такой настройке соответствуют высокие динамические показатели качества - перерегулирование Возьмем в качестве нескомпенсированной постоянной времени
Зададимся значением коэффициента передачи датчика напряжения
Теперь можно определить ПФ разомкнутого контура
После этого рассчитаем ПФ регулятора напряжения
В результате получим
где Поделив числитель ПФ
где
Анализ показывает, что РН реализует пропорционально - интегрально - дифференциальный (ПИД) закон управления.
Расчет контура регулирования скорости
Первый контур регулирования является подчиненным второму и входит в канал управления последнего в виде подсистемы (звена). С учетом этого схему контура регулирования скорости для простоты расчетов целесообразно представить в виде структуры, изображенной на рис. 5.7.
Рис 5.7. Структурная схема контура регулирования скорости
Здесь Положим, что при максимальной скорости вращения двигателя Тогда получим
Передаточная функция контура регулирования напряжения
Согласно методике коррекции с подчиненным регулированием координат в знаменателе
Далее, как и для контура напряжения необходимо сформировать ПФ объекта управления для регулятора скорости. Из рис. 5.7 следует, что она равна
В качестве малой нескомпенсированной постоянной времени
Далее можно определить ПФ регулятора скорости:
где Полученная ПФ регулятора скорости показывает, что РС также, как и РН является ПИД - регулятором:
где
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.41.80 (0.009 с.) |

 - передаточная функция РН,
- передаточная функция РН,  - ПФ делителя напряжения.
- ПФ делителя напряжения.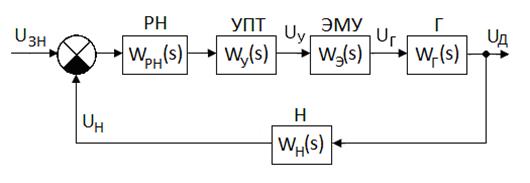
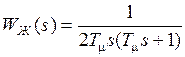 ,
, – нескомпенсированная постоянная времени.
– нескомпенсированная постоянная времени.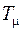 берется наименьшая постоянная времени синтезируемого контура, поэтому она часто называется малой постоянной времени. По существу
берется наименьшая постоянная времени синтезируемого контура, поэтому она часто называется малой постоянной времени. По существу  – ПФ реального интегратора. При этом желаемая ПФ замкнутой системы определяется соотношением
– ПФ реального интегратора. При этом желаемая ПФ замкнутой системы определяется соотношением ,
, .
.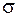 и длительность переходного процесса
и длительность переходного процесса  достаточно малы
достаточно малы  , а точность приемлема, так как контур обладает астатизмом первого порядка.
, а точность приемлема, так как контур обладает астатизмом первого порядка.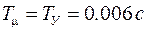 . Тогда желаемая ПФ разомкнутого контура будет иметь следующий вид:
. Тогда желаемая ПФ разомкнутого контура будет иметь следующий вид:
 , исходя из следующих соображений. Максимальное напряжение цепи обратной связи
, исходя из следующих соображений. Максимальное напряжение цепи обратной связи  , подаваемого на РН, ограничим значением
, подаваемого на РН, ограничим значением 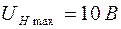 при максимальном значении напряжения генератора
при максимальном значении напряжения генератора  , которое равно максимальному напряжению, подаваемому на электродвигатель. Отсюда будем иметь
, которое равно максимальному напряжению, подаваемому на электродвигатель. Отсюда будем иметь .
. :
: .
. .
. ,
,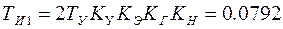 с – постоянная времени интегрирования РН.
с – постоянная времени интегрирования РН.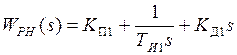 ,
, – коэффициент передачи пропорционального звена;
– коэффициент передачи пропорционального звена;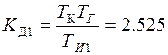 с – коэффициент передачи дифференциатора.
с – коэффициент передачи дифференциатора.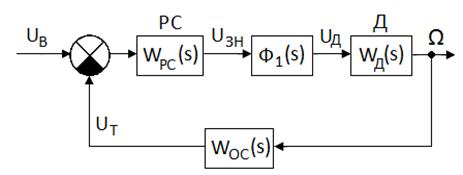
 – ПФ цепи обратной связи, включающей ТГ и его выходной делитель напряжения. Коэффициент передачи цепи обратной связи равен
– ПФ цепи обратной связи, включающей ТГ и его выходной делитель напряжения. Коэффициент передачи цепи обратной связи равен  .
. рад/с, напряжение цепи обратной связи не должно превышать максимальное значение
рад/с, напряжение цепи обратной связи не должно превышать максимальное значение  В. Чтобы система не работала в режиме насыщения, возьмем максимальную скорость с запасом
В. Чтобы система не работала в режиме насыщения, возьмем максимальную скорость с запасом  рад/с.
рад/с. в·с/рад.
в·с/рад. равна
равна .
. , т.к. он очень мал. Это приводит к небольшой погрешности при расчете регулятора скорости РС, но существенно упрощает получение его передаточной функции
, т.к. он очень мал. Это приводит к небольшой погрешности при расчете регулятора скорости РС, но существенно упрощает получение его передаточной функции  . Таким образом
. Таким образом .
.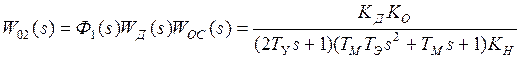 .
. берется величина
берется величина  , т.е.
, т.е.  с. Тогда желаемая ПФ контура скорости при настройке на модульный оптимум будет иметь следующий вид
с. Тогда желаемая ПФ контура скорости при настройке на модульный оптимум будет иметь следующий вид .
.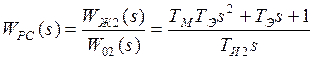 ,
, с – постоянная времени интегрирования РС.
с – постоянная времени интегрирования РС. ,
, – коэффициент передачи пропорционального звена;
– коэффициент передачи пропорционального звена; с – коэффициент передачи дифференциатора.
с – коэффициент передачи дифференциатора.


