Динамические параметры lti-моделей

 

Динамические свойства систем управления определяются величинами и соотношением полюсов (собственных значений) и нулей их lti -моделей. Поэтому для расчета нулей и полюсов были разработаны соответствующие функции.

Для определения полюсов используются функции pole и eig, которые можно применять к lti -моделям любого подкласса:

 

p=pole(sys)

p=eig(sys),

 

где р – массив полюсов в виде вектор-столбца.

При этом следует иметь в виду, что обе функции дают надежный результат только для некратных полюсов.

Пример 2.1. Вычисление полюсов непрерывной системы с ПФ Ф(s):

>> p1=pole(f)

p1 = -2.7524 +24.1162i

-2.7524 -24.1162i

-19.5359

-2.6558 + 2.4233i

-2.6558 - 2.4233i

-1.4289

-0.5474

Задание 2.1. Определите с помощью функции eig полюсы дискретной системы, заданной передаточной функцией T(z).

 

Для определения нулей используется одна функция tzero в двух вариантах обращения:

 

z=tzero(sys)

[z, gain]=tzero(sys)

 

где z – вектор возвращаемых нулей lti -модели sys; gain – коэффициент передачи в zpk -модели.

 

Пример 2.2. Вычисление нулей динамической системы с ПФ Ф(s):

>> z2=tzero(f)

z2 = -0.7166

-0.6461

Задание 2.2. Определите нули дискретной системы с ПФ Т(z).

Вместе с этими основными функциями часто используются еще две дополнительные функции для сортировки нулей и полюсов: esort – для непрерывных систем, dsort – для дискретных систем.

Функция esort используется для сортировки полюсов и нулей в порядке убывания их действительных частей, а функция dsort в порядке убывания их модулей.

Обе функции имеют две формы обращения:

 

q= esort(p), q= dsort(p)

[q, ndx]= esort(p), [q, ndx]= dsort(p),

 

где p – нули или полюсы lti -модели; q – вектор возвращаемых нулей (полюсов); ndx – вектор индексов нулей (полюсов), т.е. их порядковые номера до сортировки.

Пример 2.3. Сортировка полюсов и нулей непрерывной системы с ПФ Ф(s).

>> p3=esort(p1)

p3 = -0.5474

-1.4289

-2.6558 + 2.4233i

-2.6558 - 2.4233i

-2.7524 +24.1162i

-2.7524 -24.1162i

-19.5359

 

>> z3=esort(z2)

z3 = -0.6461

-0.7166

 

Задание 2.3. Произведите сортировку нулей и полюсов замкнутой дискретной системы с ПФ Т(z).

 

Для графического отображения расположения полюсов и нулей на комплексной плоскости используется функция pzmap, которая имеет следующий синтаксис:

 

pzmap(sys),

где sys – непрерывная или дискретная lti -модель.

Комплексная плоскость строится по команде автоматически. Полюсы на ней изображаются маркером х, а нули – маркером о.

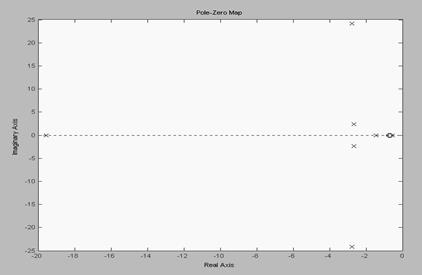
Пример 2.4. Получение схемы расположения нулей и полюсов непрерывной системы с ПФ Ф(s) на комплексной плоскости (рис.2.1) с помощью команды pzmap.

>> pzmap(f)

 

 

Рис. 2.1. Схема расположения нулей и полюсов

 

Задание 2.4. Постройте на z-плоскости план расположения нулей и полюсов дискретной системы с ПФ Т(z).

 

Имеется еще один вариант использования функции pzmap:

 

[p,z]= pzmap(sys),

 

при котором возвращаются значения полюсов и нулей lti -модели sys соответственно в виде векторов p и z, но без построения их схемы расположения на комплексной плоскости. Эта форма по существу объединяет действие функций pole и tzero.

 

Пример 2.5. Определение нулей и полюсов непрерывной системы с ПФ Ф(s) с помощью функции pzmap:

 

>> [p5,z5]= pzmap(f)

p5 = -2.7524 +24.1162i

-2.7524 -24.1162i

-19.5359

-2.6558 + 2.4233i

-2.6558 - 2.4233i

-1.4289

-0.5474

z5 = -0.7166

-0.6461

Задание 2.5. Вычислите полюсы и нули дискретной системы с ПФ Т (z) с помощью функции pzmap и сравните их значения с ранее полученными результатами.

 

Если lti -модель sys содержит комплексно сопряженные полюсы, то с помощью функции damp можно рассчитать собственные частоты ω₀ и коэффициент демпфирования ξ соответствующего им колебательного оператора s² + 2ξω₀s + ω₀².

Функция имеет три формы обращения:

 

[W,Q]= damp(sys)

[W,Q,P]= damp(sys)

damp(sys)

 

В первом случае возвращаются значения собственных частот ω₀ и коэффициентов демпфирования соответственно в виде векторов W, Q, во втором – дополнительно полюсы lti -модели в виде вектора Р, в третьем – полюсы в порядке возрастания их модуля, собственно модули и соответствующие им собственные частоты и коэффициенты демпфирования. При этом для операторов первого порядка коэффициент демпфирования принимается равным единице, а собственная частота – абсолютному значению полюса или нуля.

Для дискретной системы программа предварительно рассчитывает эквивалентные полюсы непрерывной lti -модели из соотношения z_i=exp(p_iT_s), где T_s – период квантования, а затем эквивалентные собственные частоты и коэффициенты демпфирования.

 

Пример 2.6. Расчет собственных частот и коэффициентов демпфирования непрерывной системы с ПФ Ф(s):

 

>> [W6,Q6]= damp(f)

 

W6 = 0.5474 1.4289 3.5952 3.5952 19.5359 24.2728 24.2728

Q6 = 1.0000 1.0000 0.7387 0.7387 1.0000 0.1134 0.1134

Задание 2.6.Вычислите эквивалентные значения полюсов, собственных частот и коэффициентов демпфирования дискретной системы с ПФ Т(z).

 

Кроме рассмотренных выше функций расчета динамических параметров имеется еще одна полезная функция dcgain, которая используется для вычисления коэффициента передачи lti -модели sys:

 

k= dcgain(sys).

Пример 2.7. Определение коэффициента передачи замкнутой САУ, заданной ПФ Ф(s):

 

>> k7= dcgain(f)

k7 = 9.9690

Задание 2.7. Вычислите коэффициент передачи дискретной системы с ПФ Т(z).

Частотные характеристики

 

В теории и практике систем автоматического управления наибольшее применение находят амплитудно-фазовые частотные характеристики (АФХ или их иногда называют годографами Найквиста), логарифмические частотные характеристики (диаграммы Боде) и амплитудные частотные характеристики. Для их расчета и построения в Control System Toolbox включены соответствующие функции.

Построение частотного годографа Найквиста осуществляется с помощью группы функций nyquist:

 

nyquist(sys),

nyquist(sys,dw),

 

где sys – непрерывная или дискретная lti- модель любого подкласса;

dw={Wmin, Wmax} – диапазон частот;

Wmin, Wmax – соответственно минимальная и максимальная частоты.

Частотный диапазон можно также задать с помощью массива конкретных частот dw=[w1,w2,…,wn], где n – число частот.

 

Для создания логарифмически распределенного вектора частот используется команда logspaсe. Эта функция возвращает вектор-строку логарифмически возрастающих частот:

 

 

logspaсe(log10(Wmin), log10(Wmax))

logspaсe(log10(Wmin), log10(Wmax), N),

 

где N – число точек в диапазоне частот (по умолчанию N =50).

 

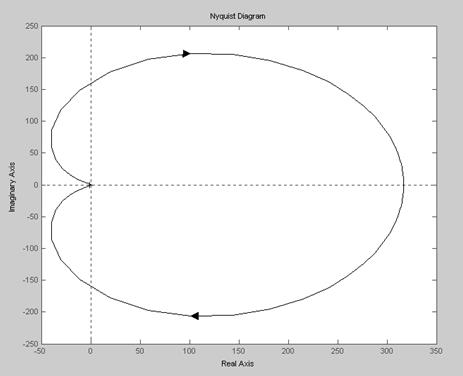
Основной функцией является nyquist(sys), в которой частотный диапазон определяется автоматически по минимальному и максимальному значениям и массива нулей и полюсов lti -модели. Если последняя содержит астатизм, то выдается предупреждающее сообщение, что на нулевой частоте характеристика равна бесконечности (неопределенное значение). Поэтому в этом случае целесообразно использовать функцию вида nyquist(sys,dw). В практических задачах функция nyquist наиболее часто применяется для построения годографа разомкнутой САУ с целью исследования устойчивости замкнутой системы с помощью критерия Найквиста.

Для дискретных систем из-за периодичности частотной характеристики АФХ рассчитывается в диапазоне от нуля до частоты Найквиста (). Если период T_s неспецифицирован, то по умолчанию принимается T_s = 1.

Пример 2.8. Построение АФХ разомкнутой системы с ПФ W(s) (рис.2.2).

>> nyquist(w)

 

 

Рис. 2.2. Амплитудно-фазовая характеристика разомкнутой системы

Задание 2.8.Постройте годограф Найквиста дискретной САУ по ПФ разомкнутой системы D(z).

 

Если требуется построить годографы Найквиста для нескольких систем в одних координатах, то можно использовать функцию nyquist в более общих формах:

 

nyquist(sys1, sys2,…,sysN)

nyquist(sys1, sys2,…,sysN, dw)

nyquist(sys1, 'plotstyle1',…,sysN, 'plotstyleN'),

 

где 'plotstyleK' – аргумент, определяющий стиль линии, т.е. цвет и тип годографа K -ой lti -модели.

Примечание. Задание стиля осуществляется в соответствии с правилами оформления графиков в MATLAB – в виде набора трех символьных маркеров, заключенных в апострофы. Один из них определяет тип линии (табл. 2.1), другой – цвет (табл. 2.2). При этом можно указывать не все маркеры. В этом случае действуют маркеры, установленные по умолчанию. Порядок маркеров в строке стиля не регламентирован, т.е. может быть произвольным.

 

Таблица 2.1

Тип линии

Маркер	Тип линии
–	непрерывная
- -	штриховая
:	пунктирная
–.	штрихпунктирная

 

Таблица 2.2

Цвет линии

Маркер	Цвет линии
c	голубой (cean)
m	фиолетовый (magenta)
y	желтый (yellow)
r	красный (red)
g	зеленый (green)
b	синий (blue)
w	белый (white)
k	черный (black)

Пример 2.9. Построение АФХ разомкнутой системы соответственно с ПФ W(s) и 0.5W(s) в одних координатах комплексной плоскости с пометкой годографа W(s) маркером 'r-', а годографа 0.5W(s) - маркером ':b' (рис.2.3).

 

>> nyquist(w,'r-',0.5*w,':b')

 

 

Рис. 2.3. Маркированные годографы Найквиста

 

Задание 2.9.Постройте годографы Найквиста для разомкнутой дискретной системы с ПФ D(z) и 0.7D(z), пометив годограф D(z) маркером ‘-.g’, а годограф 0.7D(z) – маркером ‘m- -‘.

Имеются две формы вызова функции nyquist, которые применяются для расчета годографа Найквиста без его построения:

 

[re,im,w]= nyquist(sys)

[re,im,w]= nyquist(sys,dw)

где re,im – соответственно векторы значений вещественной и мнимой частей частотной передаточной функции; w – вектор вычисленных частот (при необходимости его можно опустить).

Пример 2.10. Расчет значений действительной и мнимой частотных характеристик разомкнутой системы с ПФ W(s) в частотном диапазоне 1 - 30 рад/с.

 

>> [Re,Im]= nyquist(w,logspace(log10(1),log10(30),5))

 

Re(:,:,1) =-2.8548 Re(:,:,2) =-0.8272 Re(:,:,3) =-0.3703 Re(:,:,4) =-0.1267 Re(:,:,5) =0.0214

Im(:,:,1) =-2.4108 Im(:,:,2) =-0.8645 Im(:,:,3) =-0.2049 Im(:,:,4) =0.0310 Im(:,:,5) =-0.0070

Задание 2.10. Вычислите значения параметров АФХ для разомкнутой дискретной системы с ПФ D(z) в диапазоне частот от 0 до π/Т_s.

Построение логарифмических частотных характеристик (ЛЧХ) осуществляется с помощью функции bode, которая как и функция nyquist имеет несколько форм обращения:

 

bode(sys)

bode(sys,dw)

bode (sys1, sys2,…,sysN)

bode (sys1, sys2,…,sysN, dw)

bode (sys1, 'plotstyle1',…,sysN, 'plotstyleN')

[mag, phase, w]= bode(sys)

 

где sys – непрерывная или дискретная lti -модель; mag, phase, w – соответственно векторы амплитуд, фаз (в градусах) и частот (рад/с).

Все команды, кроме последней, осуществляют построение диаграмм Боде, представляющих совокупность двух частотных характеристик в логарифмическом масштабе: логарифмической амплитудно-частотной характеристики (ЛАЧХ) и логарифмической фазо-частотной характеристики (ЛФЧХ).

Пример 2.11. Построение логарифмических частотных характеристик для системы, заданной ПФ W(s) (рис.2.4), где команда grid on использована для нанесения сетки на график.

 

>> bode(w); grid on % Здесь команда grid on использована для % нанесения сетки на график

 

 

Рис. 2.4. Логарифмические частотные характеристики системы

 

Задание 2.11.Постройте диаграмму Боде для разомкнутой дискретной системы с ПФ D(z).

 

Использование других вариантов функции bode аналогично функции nyquist.

 

Пример 2.12. Расчет параметров ЛЧХ для разомкнутой системы с ПФ W(s).

 

>> [Mag12,Phase12,W]=bode(w,[0.5,1,4,8,17])

 

Mag12(:,:,1) = 12.7870

Mag12(:,:,2) = 3.7365

Mag12(:,:,3) = 0.6285

Mag12(:,:,4) = 0.2531

Mag12(:,:,5) = 0.0974

Phase12(:,:,1) = -146.7687

Phase12(:,:,2) = -139.8197

Phase12(:,:,3) = -141.4908

Phase12(:,:,4) = -167.2469

Phase12(:,:,5) = -214.7002

 

W = 0.5000

1.0000

4.0000

8.0000

17.0000

Задание 2.12. Постройте таблицу значений амплитуды и фазы от частоты для разомкнутой дискретной системы с ПФ D(z).

Очень часто требуется определять запасы устойчивости системы по амплитуде (модулю) и фазе. Из теории автоматического управления известно, что запас устойчивости по модулю равен значению амплитудной частотной характеристики (АЧХ) на частоте Wc, при которой фазовая частотная характеристика (ФЧХ) имеет значение -180⁰, а запас по фазе – значение разности между ФЧХ и - 180⁰ на частоте среза Wcр. Для определения этих параметров используется функция margin:

 

margin(sys)

[Gm, Pm, Wc, Wcp]= margin(sys)

 

Здесь sys – непрерывная или дискретная lti -модель;

 

Gm – запас по модулю на частоте Wc;

Pm – запас по фазе на частоте среза Wcp.

 

Команда margin(sys) строит диаграмму Боде с указанием запасов устойчивости, а функция [Gm, Pm, Wc, Wcp]=margin(sys) рассчитывает значения Gm, Pm, Wc и Wcp без построения логарифмических частотных характеристик.

Пример 2.13. Определение запасов устойчивости непрерывной системы с ПФ разомкнутой системы W(s) (рис. 2.5).

>> margin(w)

 

 

Рис. 2.5. Диаграмма Боде, построенная с помощью функций margin

Задание 2.13.Рассчитайте значения запасов устойчивости по модулю и фазе дискретной системы с ПФ разомкнутой системы D(z) без построения ЛЧХ.

При проектировании САУ часто используется показатель колебательности, который определяется в виде отношения максимального значения модуля частотной характеристики замкнутой системы к его величине на нулевой частоте (коэффициенту передачи системы).

Максимальное значение модуля частотной характеристики связано с нормой типа

- для непрерывных систем соотношением

 

 

- для дискретных систем - соотношением

В связи с этим была составлена и включена в пакет Control System Toolbox функция norm в следующих формах:

 

normsys = norm(sys, inf)

normsys = norm(sys, inf, tol)

[ninf, fpeak]= norm(sys, inf),

 

где normsys – максимальное значение АЧХ lti-модели sys;

inf – идентификатор нормы ;

tol – точность расчета нормы (по умолчанию tol =1е-2);

ninf - максимальное значение модуля частной характеристики на частоте fpeak.

При этом необходимо учитывать, что если объект sys имеет астатизм, то максимальное значение модуля АЧХ равно бесконечности.

 

Пример 2.14. Расчет максимального значения АЧХ динамической системы с ПФ замкнутой системы Ф(s).

>> [Am, Fm]=norm(f, inf)

Am =

13.7209

Fm =

1.7976

Задание 2.14. Определите значение показателя колебательности дискретной САУ с ПФ замкнутой системы Т(z), учитывая, что ее коэффициент передачи равен единице.

 

Временные характеристики

 

Для исследования динамических свойств систем автоматического управления часто используются типовые переходные режимы работы (временные характеристики). Наибольшее применение находят следующие временные характеристики:

· переходная функция (характеристика) – реакция системы на единичный скачкообразный сигнал при нулевых начальных условиях;

· весовая функция (импульсная переходная характеристика) – реакция непрерывной системы на воздействие в виде δ -импульса Дирака, а для дискретной системы – на единичный импульс.

· реакция системы на ненулевые начальные условия.

По временным характеристикам можно определить ряд качественных показателей, характеризующих динамические свойства системы управления, в частности, перерегулирование, время переходного процесса и др.

В пакете Control System Toolbox имеется ряд функций для расчета и построения временных характеристик линейных систем. Основными из них являются step, impulse, initial.

Функция step вычисляет и отображает на экране переходную характеристику lti -модели. Она имеет несколько форм:

step (sys)

step (sys,t)

step (sys1, sys2,…,sysN)

step (sys1, sys2,…,sysN, t)

step (sys1, 'plotstyle1',…,sysN, 'plotstyleN')

step (sys1, 'plotstyle1',…,sysN, 'plotstyleN', t).

 

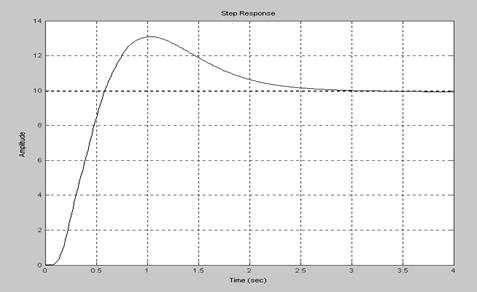
Здесь t – аргумент, задающий время моделирования в виде длительности переходного режима t=Tfinal (в секундах) или в виде вектора t=0:dt:Tfinal. Для дискретных моделей dt=T_s, а для непрерывных выбирается достаточно малым для учета быстрых изменений переходного процесса. Продолжительность моделирования при отсутствии аргумента t определяется автоматически. Остальные параметры функции step такие же, как в функциях nyquist и bode.

Пример 2.15. Построение переходной характеристики для непрерывной САУ с ПФ Ф(s) (рис.2.6).

>> step(f); grid on

 

Рис. 2.6. Переходная характеристика

 

Задание 2.15.Постройте переходную функцию для дискретной САУ, заданной передаточной функцией замкнутой системы Т(z).

Для расчета переходной характеристики без ее построения используются две дополнительные формы функции step:

 

[y, t, x]= step(sys)

[y, t, x]= step(sys, t)

 

В этом случае функция step возвращает векторы значений выхода y, времени t и переменных состояния х (количество столбцов вектора х равно размерности lti -модели). Если модель представлена в tf или zpk формах, то параметр х опускается.

Пример 2.16. Расчет переходной характеристики с шагом 0.2 с без ее построения для непрерывной САУ с ПФ замкнутой системы Ф(s).

>> [y,t]=step(f,[0:0.2:4])

 

 

y = 0 1.4753 6.1814 10.2384 12.4296 13.0739 12.8339 12.2280 11.5721 11.0248 10.6314 10.3729 10.2107 10.1104 10.0479 10.0075 9.9800 9.9607 9.9471 9.9379 9.9321

t = 0 0.2000 0.4000 0.6000 0.8000 1.0000 1.2000 1.4000 1.6000 1.8000 2.0000 2.2000 2.4000 2.6000 2.8000 3.0000 3.2000 3.4000 3.6000 3.8000 4.0000

 

Задание 2.16. Произведите вычисление переходной функции дискретной системы с ПФ замкнутой САУ T(z) без ее построения.

 

Для расчета и построения импульсной переходной (весовой) характеристики используется функция impulse в таких же формах, как и функция step:

 

impulse (sys)

impulse (sys,t)

impulse (sys1, sys2,…,sysN)

impulse (sys1, sys2,…,sysN, t)

impulse (sys1, 'plotstyle1',…,sysN, 'plotstyleN')

impulse (sys1, 'plotstyle1',…,sysN, 'plotstyleN', t)

[y, t, x]= impulse (sys)

[y, t, x]= impulse (sys, t)

 

Пример 2.17. Построение весовой характеристики для линейной непрерывной САУ с ПФ замкнутой системы Ф(s) (рис. 2.7).

>>impulse(f); grid on

 

Рис. 2.7. Весовая характеристика

 

Задание 2.17.Постройте импульсную переходную характеристику для дискретной системы с ПФ замкнутой САУ Т(z).

 

Функция initial рассчитывает и строит график реакции ss -модели sys на ненулевые начальные условия. Она имеет несколько форм, эквивалентных функциям step и impulse:

 

initial (sys,х0)

initial (sys,х0,t)

initial (sys1, sys2,…,sysN,х0)

initial (sys1, sys2,…,sysN,х0, t)

[y, t, x]= initial (sys,х0)

[y, t, x]= initial (sys,х0, t)

 

Здесь х0 – вектор начальных условий lti -модели в пространстве состояний. Смысл остальных аргументов и возвращаемых величин такой же, как у функций step и impulse.

 

Пример 2.18. Построение реакции непрерывной системы, заданной математической моделью в пространстве состояний на единичное начальное условие по последней переменной состояния, т.е. х(0)=|0 0 0 0 0 0 1 | (рис. 2.8).

 

>> sys 18=ss(f); x0=[0 0 0 0 0 0 1];initial(sys 18,x0); grid on

 

 

Рис. 2.8. Реакция по переменной состояния

 

Задание 2.18.Постройте график реакции дискретной системы с исходной ПФ T(z) и представленной ss-моделью на единичное начальное условие по второй переменной состояния х(0)=|0 1 0 0 0 0 0|.

К блоку временных функций пакета Control System Toolbox относится еще две функции: lsim – вычисление переходного процесса при произвольном входном воздействии, который формируется с помощью функции gensig – генерация периодического сигнала заданного типа (синусоида, импульсная последовательность и прямоугольный периодический сигнал). Однако на практике они используются редко, так как для моделирования систем при сложных воздействиях более удобен пакет Simulink.

Дополнительное упражнение

 

1.Открыть mat -файл из созданного в результате выполнения дополнительного задания в разделе 1.

2.Используя lti -модели, полученные для разомкнутой и замкнутой непрерывной САУ, выполнить следующие виды работ.

2.1. Определить полюсы и нули замкнутой системы.

2.2. Осуществить сортировку полюсов и нулей.

2.3. Построить схему расположения нулей и полюсов на комплексной плоскости.

2.4. Произвести расчет собственных частот и коэффициентов демпфирования замкнутой системы.

2.5. Построить годограф Найквиста разомкнутой системы и оценить по нему устойчивость замкнутой системы.

2.6. Построить ЛЧХ разомкнутой системы и оценить запас устойчивости по фазе.

2.7. Определить запас устойчивости по модулю.

2.8. Рассчитать показатель колебательности системы.

2.9. Построить переходную характеристику системы.

2.10. Построить весовую характеристику системы.

3. Повторить пункты 2.1 ÷ 2.10 для дискретного варианта САУ.

Контрольные вопросы

1.Назовите основные функции, которые используются для анализа динамических параметров lti -моделей?

2.Поясните действие функций esort и dsort?

3.С помощью каких функций можно определить полюсы и нули динамической системы?

4.Какие основные функции используются для расчета и построения временных характеристик?

5.Каким образом рассчитываются временные характеристики без их построения?

6.Как задается время расчета переходного процесса?

7.Какие функции служат для построения частотных характеристик динамических систем?

8.Как реализовать логарифмическое изменения частоты?

9.Дайте сравнительную оценку функциям nyquist и bode.

10. С помощью какой функции строится схема расположения нулей и полюсов на комплексной плоскости?

11. Поясните особенности форм обращения к функции damp.

12. Как определить коэффициент передачи системы?

13. С помощью какой функции можно оценить запас устойчивости САУ?

14. Как рассчитать показатель колебательности системы?

15. Поясните особенности использования функции initial и задания в ней начальных условий.