
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон бойля–мариотта для смеси газов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для вычисления парциальных объемов законом Бойля–Мариотта для всех газов, входящих в смесь
Уравнение состояния смеси газов
Имеется смесь из n газов, подчиняющихся уравнению состояния газа. Смесь занимает объем Vсм, м3, при давлении Рсм, Па, и температуре Тсм, К. Основываясь на законе Дальтона, можно для каждого газа написать уравнение состояния
где Ri – удельная газовая постоянная i-того компонента, Дж/(кг К).
Формулы для расчета газовых смесей.
Зависимость между массовыми и объемными долями можно получить для i-того компонента следующим образом.
Плотности компонента и смеси должны быть взяты при давлении и температуре смеси. Аналогично уравнениям (2.6) и (2.7) можно получить уравнения
Так как μ, кг/кмоль, обратно пропорционально R, Дж/(кг К), то можно записать
Или
но, так как
то
Если состав смеси задан числом киломолей, то это равносильно заданию ее объемными долями. Формулы для определения парциальных давлений будут иметь различный вид в зависимости от того, в каких долях задана смесь. Если смесь задана объемными долями, то из уравнения (2.4) следует
Если смесь задана массовыми долями
и
Задание на самостоятельную работу
1. Понятие парциального объема i-того компонента. 2. Вывод уравнения для расчета газовой постоянной для смеси газов. 3. Вывод основных формул для расчета газовых смесей. 4. Доказательство того, что задание смеси числом киломолей равносильно заданию ее объемными долями.
Вопросы для самопроверки
1. Что такое газовая смесь? 2. Дать формулировку закона Дальтона? 3. Что называется парциальным давлением? 4. Что называется массовой, объемной и мольной долями? 5. Что называется парциальным или приведенным объемом? 6. Какая существует зависимость между удельным объемом, плотностью, молекулярной массой и газовой постоянной? 7. Как производится пересчет массового состава в объемный и объемного в массовый? 8. Как определяется газовая постоянная смеси по массовым и объемным долям? 9. Как определяется парциальное давление газа в смеси по массовым и объемным долям? Лекция 3 Тема. Основные понятия теплообмена. Тепловой баланс.
План лекции
3.1. Уравнение теплового баланса 3.2. Закон Фурье 3.3. Дифференциальное уравнение теплопроводности 3.4. Теплопроводность при стационарном режиме и граничных условиях первого рода через однослойную плоскую стенку 3.5. Конвективный теплообмен 3.6. Коэффициент теплоотдачи. Дифференциальное уравнение конвективного теплообмена Теплопередача 3.7.1. Передача теплоты через многослойную плоскую стенку
Количество тепла, передаваемого в единицу времени от одного тела к другому называется тепловым потоком. При теплообмене между двумя теплоносителями происходит уменьшение энтальпии горячего теплоносителя и увеличение энтальпии холодного теплоносителя. Пусть количество горячего теплоносителя, его начальная и конечная энтальпия равны соответственно G, кг/с, I1 и I, Дж/кг, холодного g, кг/с, i и i, Дж/кг.Количество тепла передаваемое от горячего теплоносителя к холодному составляет Q, Вт, – эта величина называется тепловой нагрузкой, а потери тепла в окружающую среду Qп, Вт. Тогда уравнение теплового баланса запишется в виде
или
Если пренебречь Qп, то
или
Если в аппарате происходит охлаждение горячего теплоносителя, то I1=cг T1; I2=cг T2, где сг – удельная теплоемкость горячего теплоносителя, Дж/(кг К); Т1 и Т2 – температуры теплоносителя на входе в аппарат и выходе из него
аналогично
где сх – удельная теплоемкость холодного теплоносителя, Дж/(кг/К); t1 и t2 – температуры на входе в аппарат и выходе из него; ΔТ и Δt температурные перепады, ºС; W и w называются водяными эквивалентами, Вт/К. При конденсации парообразного теплоносителя величины I1 и I2 в уравнении (11.14) представляет собой соответственно энтальпию поступающего пара и уходящего конденсата. Если пар поступает перегретым с температурой Т1 то величина G I1 складывается из энтальпии жидкости при температуре насыщения Тн; тепла, расходуемого на испарение жидкости и равного теплу конденсации пара Qконд, а также тепла Qпер, необходимого для перегрева пара, т.е.
Величина
где Т2 – температура уходящего конденсата, ºС. Тогда уравнение (1) запишется
Тепло, отдаваемое при охлаждении перегретого пара, равно теплу, затраченному на перегрев при его получении, и составляет
Тепло, отдаваемое при конденсации пара, равно теплу, расходуемому на испарение жидкости
Тепло, отдаваемое при охлаждении конденсата, составляет
В этих уравнениях сп и сж – удельные теплоемкости пара и жидкости, Дж/(кг К); r – теплота испарения, Дж/кг. При конденсации насыщенного пара без охлаждения конденсата
Закон Фурье.
Для распространения теплоты в любом теле или пространстве необходимо наличие разности температур в различных точках тела. Связь между количеством теплоты
где Количество теплоты, проходящей через единицу изотермной поверхности в единицу времени, называют плотностью теплового потока q, Вт/м2
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.54 (0.009 с.) |

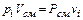 , (2.4)
, (2.4) (2.5)
(2.5)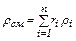 (2.6)
(2.6)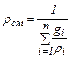 (2.7)
(2.7)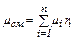 (2.8)
(2.8)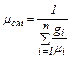 (2.9)
(2.9)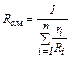 (2.10)
(2.10)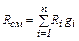 (2.11)
(2.11)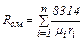 (2.12)
(2.12)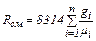 (2.13)
(2.13)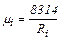 ,
,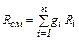 (2.14)
(2.14)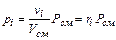 (2.15)
(2.15)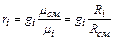 (2.16)
(2.16)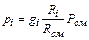 (2.17)
(2.17)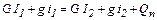 (3.1)
(3.1)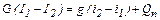 (3.2)
(3.2)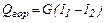 (3.3)
(3.3)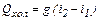 (3.4)
(3.4)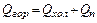 (3.5)
(3.5)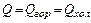 (3.6)
(3.6)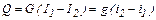 (3.7)
(3.7)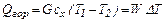 (3.8)
(3.8)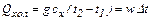 (3.9)
(3.9)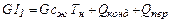 (3.10)
(3.10)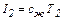
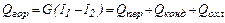 (3.11)
(3.11)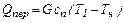 (3.12)
(3.12)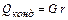 (3.13)
(3.13)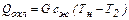 (3.14)
(3.14)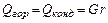 (3.15)
(3.15)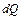 , Дж, проходящим через элементарную площадку
, Дж, проходящим через элементарную площадку 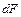 , м, расположенную на изотермной поверхности за промежуток времени
, м, расположенную на изотермной поверхности за промежуток времени 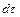 , с, и градиентом температуры
, с, и градиентом температуры 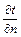 , К м, устанавливается законом Фурье
, К м, устанавливается законом Фурье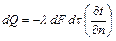 (3.16)
(3.16)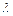 – коэффициент теплопроводности, Вт/(м К).
– коэффициент теплопроводности, Вт/(м К).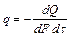 или
или 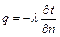 (3.17)
(3.17)


