
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деградация энергии при протекании необратимых процессов в изолированных системах.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Все реально протекающие процессы – необратимые, и в каждом случае необратимость является причиной снижения совершенства процесса. Это происходит не из-за потери энергии, а из-за понижения ее качества, так как в необратимых процессах энергия не исчезает, а обесценивается. Так, например, дросселирование рабочего тела не изменяет его энергии (iн=iк), а снижает ее пригодность к совершению работы при использовании в теплообменниках. Таким образом, каждое необратимое явление – это причина безвозвратной потери энергии. Так как всякая необратимость приводит к уменьшению полезной работы, то увеличение энтропии изолированной системы из-за необратимости протекающих в ней термодинамических процессов может служить мерой потери максимально полезной работы lmax, Дж/кг, которую могла бы совершить система при протекании в ней обратимых термодинамических процессов. При необратимых термодинамических процессах потерянная работа самопроизвольно превращается в теплоту, которая также самопроизвольно переходит к телам с более низкой температурой, увеличивая их энтропию (а следовательно, и системы) на значение Тогда, согласно уравнению (5.7) необходимое превращение работы в теплоту
где Т0 – низшая температура в изолированной системе (при анализе термодинамических процессов в качестве такой температуры принимают температуру окружающей среды), К
Выражение (8.1), характеризующее потерю максимальной работы (работоспособности) из-за необратимости, носит название уравнения Гюи – Стодолы. Тогда фактически полезная работа l0, Дж/кг, с учетом уравнения (8.1) будет выражаться уравнением
Максимально возможную работу, которую может совершить система, состоящая из источника энергии и окружающей среды, называют эксергией е, Дж/кг (е=lmax). В самом общем смысле эксергия вещества есть максимальная работа, которую оно может совершить в обратимом процессе с окружающей средой в качестве источника даровой теплоты, если в конце этого процесса все участвующие в нем виды материи переходят в состояние термодинамического равновесия со всеми компонентами окружающей среды.
Эксергия делится на два основных вида: эксергия видов энергии, не характеризуемых энтропией, для которых она равна самой энергии Э, Дж/кг, е=Э (механическая, электрическая и др.), и эксергия видов энергии, характеризуемых энтропией (внутренняя энергия, энергия излучения, термомеханическая, нулевая). Эксергия последних видов энергии подразделяется на эксергию вещества в замкнутом объеме, эксергию потока вещества и эксергию потока энергии. Эксергия вещества в замкнутом объеме состоит из термомеханической и нулевой. Эксергия потока энергии состоит из эксергии теплового потока и эксергии излучения. Эксергия вещества в замкнутом объем еv, Дж/кг, рассматривается в закрытых системах. Определим термомеханическую эксергию вещества в замкнутом объеме, т.е. максимальную работу которую может совершить вещество с начальными параметрами p, v, T, u, i, s при обратимом процессе в равновесие с окружающей средой, когда его параметры будут иметь значения p0, v0, T0, u0, i0, s0. Для того чтобы вещество перешло в равновесие с окружающей средой, необходимо изменить его внутреннюю энергию за счет подвода (или отвода) к нему теплоты либо за счет совершения им работы, поскольку в соответствии с первым законом термодинамики
В обратимом процессе подвод теплоты к веществу либо отвод от него теплоты в окружающую среду происходит при постоянной температуре, равной температуре окружающей среды Т0, т.е.
Тогда эксергия вещества в замкнутом объеме будет равна работе за вычетом работы, затрачиваемой веществом на преодоление им давления окружающей среды, т.е
где
и следовательно ev является параметром состояния вещества и среды – эксергической функцией. Для определения термомеханической эксергии потока вещества е, Дж/кг, требуется найти максимальную работу его при обратимом переходе от данного состояния, характеризующегося параметрами p, v, T, u, i, s к равновесному состоянию со средой, т.е. с параметрами p0, v0, T0, u0, i0, s0. Очевидно, эксергия потока вещества отличается от эксергии вещества в замкнутом объеме на величину работы, связанной с перемещением потока. Для конечного изменения состояния эта работа будет равна работе за вычетом работы, затрачиваемой на преодоление давления среды
Обычно в расчетах определяют разность величин Δev и Δe в двух состояниях системы.
Эксергия теплового потока eq, Дж/кг,
где В частном случае при T=idem и
Функция τе имеет универсальное значение: она пригодна для оценки максимальной работоспособности в круговых и разомкнутых термодинамических процессах. Можно доказать, что частная производная термомеханической эксергии потока по энтальпии при постоянном давлении равна τе, т.е.
Так как
т.е. изменение эксергии потока рабочего тела в изобарном процессе равно эксергии eq связанного с этим процессом теплового потока. Следовательно, во всех процессах теплообмена, протекающих при постоянном давлении, эксергию теплового потока можно вычислять по разности эксергий потока вещества Δе. Это значительно упрощает расчеты, когда точный расчет непосредственно eq является трудоемким, как, например, при переменной температуре. Эксергия излучения eε определяется максимальной работой, которая может быть совершена в обратимом процессе приведения этого излучения в состояние равновесия с окружающей средой (при Т0). Ее вычисляют по уравнению
где ε – степень черноты поверхности; С0 – коэффициент лучеиспускания абсолютно черного тела, Вт/(м2 К4).
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.35.16 (0.011 с.) |

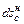 , Дж/(кг К).
, Дж/(кг К).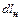 , Дж/кг, можно записать в виде
, Дж/кг, можно записать в виде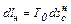 (6.1)
(6.1)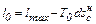 (6.2)
(6.2)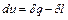
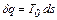 .
.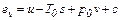 (6.3)
(6.3)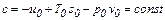 ,
,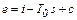 (6.4)
(6.4)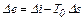 . (6.5)
. (6.5)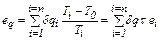 (6.6)
(6.6)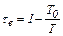 называется эксергической температурной функцией.
называется эксергической температурной функцией.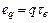 (6.7)
(6.7)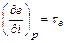 (6.8)
(6.8)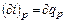 или
или 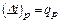 , то из уравнений (6.6) и (6.7) следует, что
, то из уравнений (6.6) и (6.7) следует, что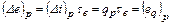 , (6.9)
, (6.9)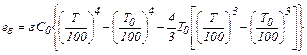 (6.10)
(6.10)


