
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение уравнений в частных производных.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
К уравнениям в частных производных приводят задачи газодинамики, теплопроводности, переноса излучения, электромагнитных полей, процессов переноса в газах, и др. Независимыми переменными в физических задачах обычно являются время t, координаты
где U – температура, Для решения дифференциальных уравнений в частных производных применяется сеточный метод, суть которого – в разбиении области, в которой ищется решение, сеткой узлов заданной конфигурации, после чего составляется разностная схема уравнения и находится его решение, например методом разностной аппроксимации. Рассмотрим в качестве примера одномерную задачу, близкую по смыслу к (17):
Здесь 0 ≤ x ≤ a, 0 ≤ t ≤ T. Граничные условия:
Для одной и той же задачи можно составить много разностных схем. Метод разностной аппроксимации заключается в том, что каждая производная, входящая в дифференциальное уравнение и краевые условия, заменяется разностным выражением, включающим в себя только значения в узлах сетки. Введем равномерную прямоугольную сетку по x и t с шагом h и τ соответственно и заменить производные соответствующими разностными отношениями. Тогда
Здесь 1 ≤ k ≤ N -1 – число точек по координате x; 0 ≤ m ≤ M – число точек по координате t. Число неизвестных в (19) больше числа уравнений, недостающие уравнения выводятся из начальных и граничных условий:
Схема (19) содержит в каждом уравнении несколько неизвестных значений функции. Такие схемы называют неявными. Для фактического вычисления решения следует переписать схему так:
Теперь схема представляет собой систему линейных уравнений для определения величин
Другим вариантом решения сеточной задачи является использование интегро-интерполяционных методов (методов баланса), в которых дифференциальное уравнение интегрируют по ячейке сетки, приближенно вычисляя интегралы по квадратурным формулам. Алгоритм метода РК 4 порядка 19. Построить сетку с шагом 20. Решение дифференциального уравнения ищется в виде сеточной функции. Значение
где
21. Для проверки сравнить значения приближенного решения со значениями точного решения в узлах сетки.
Вопросы теста 1. Численные методы – это… (выберите правильные определения) a. методы приближённого решения математических задач, сводящиеся к выполнению конечного числа элементарных операций b. методы интерполяции решения некоторой корректно поставленной задачи. c. методы, в которых решение получается как предел некоторой последовательности значений, причем значения выражаются через элементарные функции и т.п. d. это алгоритмы вычисления приближенных (а иногда—точных) значений искомого решения задачи на некоторой выбранной сетке значений аргумента х. e. методы решения математических задач в численном виде.
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

 , скорости частиц
, скорости частиц 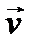 . Пример – уравнение теплопроводности
. Пример – уравнение теплопроводности , (17)
, (17) – теплоемкость,
– теплоемкость,  – коэффициент теплопроводности, q – плотность источников тепла.
– коэффициент теплопроводности, q – плотность источников тепла. . (18)
. (18)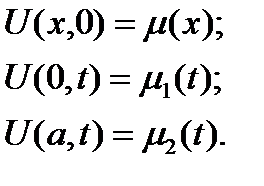
 . (19)
. (19)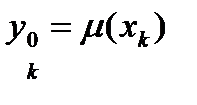 ; 0 ≤ k ≤ N.
; 0 ≤ k ≤ N. ;
;  ; 0 ≤ m ≤ M.
; 0 ≤ m ≤ M. , где 1 ≤ k ≤ N -1.
, где 1 ≤ k ≤ N -1. ;
;  . (20)
. (20) ; правые части этих уравнений известны, поскольку содержат значения решений для предыдущего индекса времени.
; правые части этих уравнений известны, поскольку содержат значения решений для предыдущего индекса времени. . Значение шага выбирается из соображений требуемой точности, учитывая, что порядок точности метода
. Значение шага выбирается из соображений требуемой точности, учитывая, что порядок точности метода  . Левая граница отрезка, на котором строится сетка,
. Левая граница отрезка, на котором строится сетка,  задана начальными условиями задачи Коши.
задана начальными условиями задачи Коши. известно из начальных условий, все следующие значения
известно из начальных условий, все следующие значения 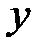 рассчитываются по формулам Рунге–Кутта:
рассчитываются по формулам Рунге–Кутта: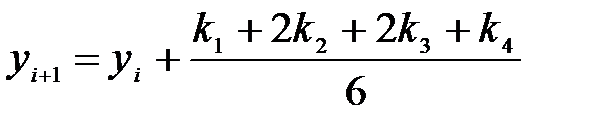 ,
, ,
, ,
, ,
, ,
, – правая часть дифференциального уравнения;
– правая часть дифференциального уравнения; – вспомогательные функции, значения которых вычисляются предварительно для каждого
– вспомогательные функции, значения которых вычисляются предварительно для каждого  .
.



