
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если в двух соседних узлах функция будет иметь разные знаки, то между этими узлами лежит нечетное число корней уравнения (по меньшей мере один).
3) Вычисление каждого (или интересующего нас) корня уравнения с требуемой точностью. Уточнение происходит с помощью методов, изложенных ниже.
Два этапа решения: 1. На первом этапе локализуют корни (т.е. прикидывают, в какие интервалы облшасти определения попадают корни, чтобы далее сужать поиск, производя уточнение не на всей области определения, а только в пределах нескольких узких отрезков – это ускоряет процесс поиска решения). Области локализации (отрезки) стараются выбрать минимальными, т.е. так, чтобы в в каждый отрезок локализации попал ТОЛЬКО один корень уравнения f (x) = 0 (иначе есть риск найти не все корни уравнения). Локализация корней может производиться (1) графически или (2) аналитически. (1) В первом случае строят график функции f (x) и выделяют те промежутки 0Х, где график пересекает ось Ox. Если построение графика y = f (x) затруднительно, но f (x) = 0 представляется в виде f1(x) = f2 (x), то строят графики y = f1(x), y = f2 (x) и за начальное Х берут промежутки/точки пересечения этих графиков. (2) Для аналитического отделения корней находят все критические точки функции f (x), т.е. точки, в которых производные равны нулю или не существуют. Для этого f (x) дифференцируют, приравнивают производную к нулю и решают полученное уравнение относительно x. Кроме того, определяют все точки, где производная может не существовать. В этих (критических) точках или в непосредственной близости от них определяют знак функции f (xi). Затем строят ряд знаков функции в критических точках, включая в рассмотрение и
1. Графический способ: Построить график f(x) и прикинуть отрезки, где график пересекает ось ОХ (см. рисунок справа – 3 пересечения графика f(x) с осью ОХ говорят о наличии 3 действительных корней у уравнения f(x)=0. Правда, мнимые корни таким графиком выявить невозможно). 2. Если график построить затруднительно, но можно представить f(x) в виде суммы 2 более простых функционалов f(x)=g(x)+h(x), то можно построить графики g(x) и h(x) и прикинуть точки (или отрезки) оси х, где графики пересекаются – там есть корни (Рис. Второй справа ниже, 2 линии – синяя и красная – это 2 функции, в сумму которых оказалось с возможным разложить f(x) (если такая возможность вообще есть) – здесь корнями являются 3 точки пересечения этих графиков друг с другом. Их и надо уточнить до заданного уровня погрешности).
3. Аналитический способ: подставить несколько значений Х в f(x) (включая оба края области определения), прикидывая, какой знак в этих точках имеет (т.е. f(x)>0 или f(x)<0). Если на соседних таких точках знаки различны – значит где-то между ними есть корень (или корни) f(x)=0. 4. Найти стационарныеточки (т.е. те х, где производная f / (x)=0) - они тоже могут быть краями интервалов, где есть корни.
2. На втором этапе численного решения нелинейного уравнения итерационно уточняют корни с заданной точностью. Способы уточнения различны: 1) путем перебора всех возможных значений аргумента (с малым шагом) из отрезка локализации с проверкой наличия решения; 2) либо замена нелинейной функции f более простой функцией (линейной, параболической), близкой к исходной, и поиск ее корня итерационными процедурами; 3) либо сведение нелинейного уравнения f (x) = 0 к виду f1(x) = f2 (x) и обеспечение в нем равенства итерационными процедурами. Условием окончания процесса решения уравнения (т.е. получения корня x* с заданной погрешностью) может быть одно из двух возможных условий:
Численные методы уточнения корней (2 этапа): 1. Метод половинного деления – с простым способом выбора пробной точки путем деления промежутка существования корня пополам. Алгоритм такой: На каждом шаге итерации делят отрезок локализации пополам, за оценку корня берут середину отрезка:
2. Метод касательных (Ньютона). 3. Метод простых итераций. f(x) разлагают в форму: x=g(x). - В таком случан решение ищут итерационно: xn+1=g(xn). За начальное х0 берут какое-нибудь значение из интервала локализации корня. Известно, что метод сходится со скоростью геометрической последовательности и справедлива оценка погрешности: Можно взять за критерий сходимости итерационного процесса к решению 4. Метод хорд. расчетная формула для уточняемого корня на очередной итерации выглядит так: 5. Метод ложного положения.
Метод дихотомии (бисекций).
Итерации продолжаются, пока длина отрезка не станет меньше 2ξ – заданной точности. Тогда середина последнего отрезка даст значение корня с требуемой точностью. В качестве иного критерия можно взять | f (x)| ≤ ξy. Скорость сходимости метода невелика, однако он прост и надежен. Метод неприменим к корням четной кратности. Если на отрезке несколько корней, то заранее неизвестно, к какому из них сойдется процесс. Если на заданном интервале предполагается несколько корней, то существует возможность последовательно исключать найденные корни из рассмотрения. Для этого воспользуемся вспомогательной функцией Метод хорд. Идея метода проиллюстрирована рисунком. Задается интервал [ x 0, x 1], на котором f (x 0) f (x 1) ≤ 0, между точками x 0 и x 1 строится хорда, стягивающая f (x). Очередное приближение берется в точке x 2, где хорда пересекает ось абсцисс. В качестве нового интервала для продолжения итерационного процесса выбирается тот, на концах которого функция имеет разные знаки. Условия выхода из итерационного цикла:
Для вывода итерационной формулы процесса найдем точку пересечения хорды (описываемой уравнением прямой) с осью абсцисс: ax 2 + b = 0, где Отсюда легко выразить Метод хорд в большинстве случаев работает быстрее, чем метод дихотомии. Недостатки метода те же, что и в предыдущем случае.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.190.167 (0.04 с.) |
 . Анализируя этот ряд, и по числу смен знаков определяют количество корней и интервалы локализации корней: на левой и правой границах такого интервала функция f (x) должна иметь разные знаки. Одна из проблем, в которую упирается решение задачи локализации корней, – это практическая невозможность точного вычисления значения функций.
. Анализируя этот ряд, и по числу смен знаков определяют количество корней и интервалы локализации корней: на левой и правой границах такого интервала функция f (x) должна иметь разные знаки. Одна из проблем, в которую упирается решение задачи локализации корней, – это практическая невозможность точного вычисления значения функций. итерации. (Т.е. или близость к нулю левой части уравнения, или близость друг к другу двух значений x, между которыми находится решение. Второе условие во многих случаях можно использовать, не зная точного значения корня, путем замены
итерации. (Т.е. или близость к нулю левой части уравнения, или близость друг к другу двух значений x, между которыми находится решение. Второе условие во многих случаях можно использовать, не зная точного значения корня, путем замены  ).
). . Если значение f(xn) в точности =0, то корень считается найденным, итерации прерывают. Если же значение f(xn) не 0, то смотрят знак. (т.к. f(xn)<0 или f(xn)>0), и берут за новые, более узкие границы интервала локализации те, где f(x) принимает разные знаки. Затем весь блок повторяется. Критерий окончания итераций:
. Если значение f(xn) в точности =0, то корень считается найденным, итерации прерывают. Если же значение f(xn) не 0, то смотрят знак. (т.к. f(xn)<0 или f(xn)>0), и берут за новые, более узкие границы интервала локализации те, где f(x) принимает разные знаки. Затем весь блок повторяется. Критерий окончания итераций:  , где
, где  - заданная погрешность.
- заданная погрешность. . (Начальное приближение решения x0 берут таким, чтобы
. (Начальное приближение решения x0 берут таким, чтобы  , иначе метод может не сойтись к решению (сходимость зависит от близости начального приближения x0 к корню).) Критерий окончания итерационного процесса уточнения корня:
, иначе метод может не сойтись к решению (сходимость зависит от близости начального приближения x0 к корню).) Критерий окончания итерационного процесса уточнения корня:  . (Точность задается изначально).
. (Точность задается изначально). . Если можно подобрать такую константу q, чтобы |g/(x)|<=q<1, то метод гарантированно сходится (иногда может сойтись, даже если условие |g/(x)|<1 не выполняется).
. Если можно подобрать такую константу q, чтобы |g/(x)|<=q<1, то метод гарантированно сходится (иногда может сойтись, даже если условие |g/(x)|<1 не выполняется). : на отрезке локализации. Критерием окончания итераций считают выполнение условия:
: на отрезке локализации. Критерием окончания итераций считают выполнение условия:  где
где  - заданная погрешность.
- заданная погрешность. Метод хорд сходится медленнее, может вовсе не сойтись, во избежание чего начальное значение x0 (и x1) берут таким, чтобы
Метод хорд сходится медленнее, может вовсе не сойтись, во избежание чего начальное значение x0 (и x1) берут таким, чтобы  . Сходимость зависит от близости начального приближения x0 к корню. Критерий окончания итераций тот же
. Сходимость зависит от близости начального приближения x0 к корню. Критерий окончания итераций тот же 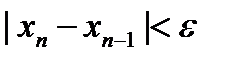 .
. . Критерий окончания
. Критерий окончания , где
, где  – только что найденный корень. Для функций f (x) и g (x) совпадают все корни, за исключением
– только что найденный корень. Для функций f (x) и g (x) совпадают все корни, за исключением  (в этой точке полюс функции g (x)). Для достижения требуемой точности рекомендуется грубо приблизиться к корню по функции g (x), а затем уточнить его, используя f (x).
(в этой точке полюс функции g (x)). Для достижения требуемой точности рекомендуется грубо приблизиться к корню по функции g (x), а затем уточнить его, используя f (x). или
или ; b = f (x 0) – ax 0.
; b = f (x 0) – ax 0. .
.


