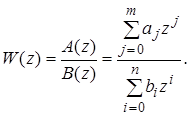Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Учет экстраполятора при вычислении Z- передаточных функций.Содержание книги
Поиск на нашем сайте Однако предположение о том, что передаточная функция W(p) ПНЧ есть дробно-рациональное выражение, не всегда выполняется. Как отмечалось ранее
где
Рассмотрим этот случай и определим для него порядок нахождения Z-передаточной функции W(z). Пусть
где
Тогда
или
В соответствии со свойствами
Найдем
Пользуясь таблицей
Подставив выражение (18) в формулу (17), найдем
т.е. получена формула для вычисления Z-передаточной функции W(z) разомкнутой системы. Отметим, что при
Здесь под знаком В общем случае для определения Z-передаточной функции W(z) можно использовать зависимость, полученную ранее в курсе «Математические основы ТАУ»:
где si – полюсы передаточной функции W(s) ПНЧ ( Следует, однако, иметь в виду, что формула (20) справедлива, если выполняется условие
Например, если передаточная функция ПНЧ имеет вид
В случае, если передаточная функция ПНЧ содержит выражение 1-е-Tp, ее можно представить в виде
где Тогда
и
где
Пример вычисления Z –передаточной функции. Найдем Z-передаточную функцию разомкнутой системы, состоящей из ИЭ с экстраполятором нулевого порядка и непрерывной части с передаточной функцией Передаточная функция ПНЧ имеет вид
Для нахождения W(z) применим формулу (23):
Полюсы выражения Тогда получим
Отсюда следует
Этот же результат можно получить с помощью таблицы
Проводя разложение на простейшие дроби, найдем
Отметим некоторые свойства Z-передаточных функций. Передаточная функция есть дробно-рациональная функция z. При использовании модифицированного Z-преобразования числитель этой функции зависит от e. Порядком передаточной функции Полюсы
Рассмотрим задачу определения реакции дискретной системы с передаточной функцией
Таким образом, если Z-преобразование выходной величины известно, процесс на выходе может быть найден по формуле обратного Z-преобразования:
Для нахождения
где Для вычисления обратного Z-преобразования, кроме того, может быть использовано разложение изображения в ряд Лорана [4]. Наконец, по известной Z-передаточной функции нетрудно составить соответствующее разностное уравнение импульсной системы. Пусть
Тогда уравнение (25) можно переписать в виде
Переходя к оригиналам и учитывая теорему о смещении аргумента решетчатой функции, получим
Это соотношение представляет собой разностное уравнение системы, с помощью которого можно рассчитать процесс на выходе дискретной САУ. Лекция 5
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 283; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ,
,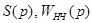 передаточные функции формирователя и собственно непрерывной части соответственно. Если
передаточные функции формирователя и собственно непрерывной части соответственно. Если 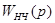 обычно является дробно-рациональной функцией, то
обычно является дробно-рациональной функцией, то  будет таковой лишь при некоторых упрощающих предположениях (см. [4]). Обычно
будет таковой лишь при некоторых упрощающих предположениях (см. [4]). Обычно  .
.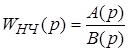 , (16)
, (16)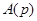 ,
, 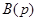 - многочлены степени m и n соответственно. Пусть
- многочлены степени m и n соответственно. Пусть 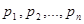 - полюсы передаточной функции (16). Считая, что все полюсы первого порядка, разложим выражение (16) на простейшие дроби:
- полюсы передаточной функции (16). Считая, что все полюсы первого порядка, разложим выражение (16) на простейшие дроби: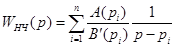 .
.
 .
.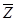 -преобразования множитель
-преобразования множитель  может быть вынесен за знак преобразования (см. курс “Математические основы ТАУ” или [6,прил.2]). Тогда
может быть вынесен за знак преобразования (см. курс “Математические основы ТАУ” или [6,прил.2]). Тогда (17)
(17) . Очевидно, что
. Очевидно, что .
. (18)
(18)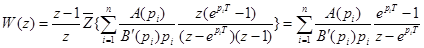 , (19)
, (19)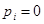 , а также при наличии кратных полюсов в формуле возникают неопределенности. Они могут раскрываться обычным способом, по правилу Лопиталя. Кроме того, формулу (17)) можно записать в виде
, а также при наличии кратных полюсов в формуле возникают неопределенности. Они могут раскрываться обычным способом, по правилу Лопиталя. Кроме того, формулу (17)) можно записать в виде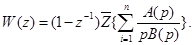
 так, как излагалось выше (используя разложение выражения на простейшие дроби), можно легко найти Z -передаточную функцию разомкнутой системы.
так, как излагалось выше (используя разложение выражения на простейшие дроби), можно легко найти Z -передаточную функцию разомкнутой системы. (20)
(20)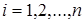 ).
). (21)
(21)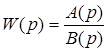 и степень многочлена
и степень многочлена  превосходит степень
превосходит степень 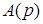 не менее чем на 2 порядка, то условие (21 выполняется, и тогда из зависимости (20) получим
не менее чем на 2 порядка, то условие (21 выполняется, и тогда из зависимости (20) получим (22)
(22)
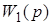 - дробно-рациональная функция.
- дробно-рациональная функция.
 (23)
(23)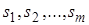 - полюсы функции
- полюсы функции  .
.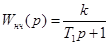 .
.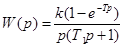 .
. .
. следующие:
следующие: 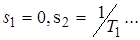 .
.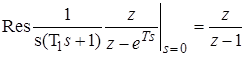 ;
; 
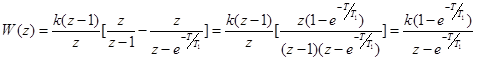
 .
.
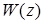 назовем степень n ее знаменателя. Порядок дискретной передаточной функции равен степени знаменателя передаточной функции непрерывной части системы
назовем степень n ее знаменателя. Порядок дискретной передаточной функции равен степени знаменателя передаточной функции непрерывной части системы  .
.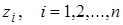 Z-передаточных функций
Z-передаточных функций 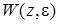 связаны с полюсами
связаны с полюсами 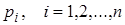 передаточной функции
передаточной функции 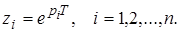 (24)
(24)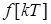 . Определив Z-преобразование входного сигнала
. Определив Z-преобразование входного сигнала  , запишем уравнение системы в изображениях:
, запишем уравнение системы в изображениях: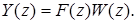 (25)
(25)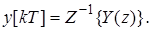
 можно применить известную формулу
можно применить известную формулу
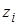 - полюсы функций
- полюсы функций