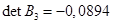Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические критерии устойчивости импульсных систем.Содержание книги
Поиск на нашем сайте
План лекции: 1. Переход к алгебраическим критериям устойчивости непрерывных систем. 2. Критерий Шура-Кона.
Переход к алгебраическим критериям устойчивости непрерывных систем. Непосредственное вычисление корней характеристического уравнения представляет собой громоздкую операцию. Поэтому важно иметь критерии устойчивости, позволяющие установить факт устойчивости многочлена без вычисления его корней. Рассмотрим характеристическое уравнение системы
Для оценки устойчивости могут использоваться критерии устойчивости непрерывных систем. Используем преобразование
которое переводит внутренность единичного круга плоскости “z”,
откуда следует, что при
или
где коэффициенты Таким образом, необходимым и достаточным условием устойчивости импульсной системы становится расположение корней Пример. Пусть характеристическое уравнение системы имеет вид
Оценим устойчивость такой системы. С использованием преобразования (51) характеристическое уравнение примет вид
Преобразовав левую часть, окончательно получим
Для оценки расположения корней последнего уравнения применим критерий Гурвица. Составим определитель Гурвица
Легко видеть, что
Критерий Шура-Кона. Для оценки устойчивости может использоваться также алгебраический критерий Шура - Кона. Рассмотрим характеристическое уравнение (50) и составим из его элементов следующую последовательность матриц:
Составим из матриц
Для обеспечения устойчивости импульсной системы с характеристическим уравнением (50) необходимо и достаточно, чтобы число перемен знака в последовательности
было равно n, т.е. степени характеристического уравнения. Иначе, должно выполняться условие:
Особенностью использования критерия Шура - Кона и его существенным неудобством является необходимость вычисления определителей высокого порядка. Рассмотрим пример применения критерия Шура – Кона для исследования устойчивости импульсной системы. Пусть характеристическое уравнение системы имеет вид:
Составляем последовательно:
Используя критерий Шура-Кона, можно заключить, что система с данным характеристическим уравнением устойчива. Лекция 11
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 (50)
(50) , (51)
, (51) в левую полуплоскость плоскости “ w ”, Re w <0. Действительно, пусть w = u+iv, тогда
в левую полуплоскость плоскости “ w ”, Re w <0. Действительно, пусть w = u+iv, тогда
 , при
, при 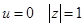 , при
, при  . После преобразования (51) характеристическое уравнение (50) принимает вид
. После преобразования (51) характеристическое уравнение (50) принимает вид
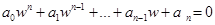 , (52)
, (52) выражаются через коэффициенты
выражаются через коэффициенты 
 уравнения (52) в левой полуплоскости плоскости. Для этого могут использоваться известные критерии устойчивости непрерывных систем (Рауса, Гурвица, Михайлова и др.). Недостатком такого подхода является трудность применения этих критериев для систем высокого порядка из-за громоздких преобразований.
уравнения (52) в левой полуплоскости плоскости. Для этого могут использоваться известные критерии устойчивости непрерывных систем (Рауса, Гурвица, Михайлова и др.). Недостатком такого подхода является трудность применения этих критериев для систем высокого порядка из-за громоздких преобразований.
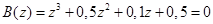



 (
( - главные диагональные миноры определителя), т.е. импульсная система устойчива.
- главные диагональные миноры определителя), т.е. импульсная система устойчива.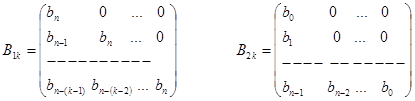
 и
и  матрицу
матрицу  размерности (2k´2k)
размерности (2k´2k) , k=1,2,…,n.
, k=1,2,…,n.
 для нечетных k;
для нечетных k; для четных k.
для четных k. .
.

 ,
, ,
, ,
, 

 0,2841,
0,2841,