
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения о дискретных автоматических системахСтр 1 из 24Следующая ⇒
Лекции по курсу «Системы цифрового управления»
Лекция 1 Общие сведения о дискретных автоматических системах План лекции 1. Квантование по времени и по уровню. 2. Виды импульсной модуляции. 3. Импульсные и цифровые методы в системах автоматического управления (САУ). Квантование по времени и по уровню. В непрерывных автоматических системах, изучавшихся в курсе "Основы ТАУ", сигналы, поступающие на входы и выходы элементов САУ, являются, как правило, непрерывными функциями времени. Однако во многих случаях оказывается выгодным переход от непрерывного к дискретному способу представления и преобразования информации. Этот переход осуществляется дискретизацией непрерывного сигнала, т.е. заменой непрерывной функций f(t) дискретными значениями f1,f2,...,fn,... Дискретизация (квантование) непрерывного сигнала может осуществляться по времени, по уровню или и по времени и по уровню. Дискретизация сигнала по времени состоит в замене непрерывного сигнала (рис.1,а) дискретными значениями, взятыми в определенные, заранее заданные моменты времени. Обычно эти момента времени равноудалены друг от друга на величину Т, которая называется интервалом квантования или периодом дискретности (рис.1,б). В этом случае последовательность {fn}, n=1,2,3..., определяется формулой
Рис.1 Дискретизация по уровню предполагает замену непрерывного сигнала числовой последовательностью f1, f2,.., fn,..., элементы которой могут принимать лишь заранее определенные, обычно равноотстоящие друг от друга значения (рис.1, в). Моменты времени, в которые происходит смена уровней, определяются видом непрерывного сигнала f(t) и заранее неизвестны. Дискретизация и по времени и по уровню совмещает в себе изложенные выше два способа формирования последовательности {fn},n=1,2... При этом непрерывный сигнал заменяется дискретной последовательностью {fn}, n=1,2… взятой в заранее заданные моменты времени, и каждый элемент этой последовательности округляется до ближайшего к нему значения уровня из числа разрешенных (рис.1,г). Обычно применяют следующую классификацию дискретных систем: - импульсные системы, в которых осуществляется дискретизация хотя бы одной из переменных системы по времени;
- релейные системы, в которых осуществляется дискретизация по уровню; - цифровые системы, в которых осуществляется дискретизация сигналов и по времени и по уровню. Из приведенных трех типов дискретных систем релейные САУ обычно рассматриваются как непрерывные системы с разрывной нелинейностью. В данном курсе ограничимся изучением импульсных и цифровых систем, особенности динамики которых определяются дискретизацией по времени.
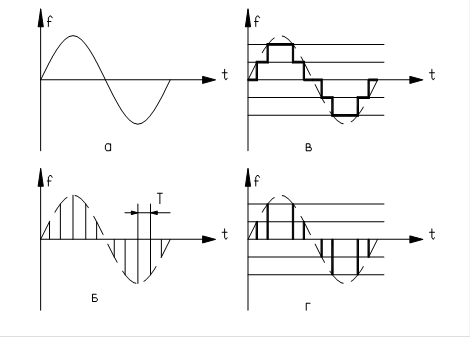
Виды импульсной модуляции. При дискретизации по времени непрерывная функция заменяется своими дискретами, выделенными в определенные моменты времени. Однако на практике нельзя реализовать решетчатую функцию с бесконечно малым временем существования каждого выделенного значения. При конечном времени работы технических устройств получается последовательность импульсов определенной длительности, промодулированная выделенными дискретами непрерывной функции. В теории дискретных систем принято выделять импульсный элемент (ИЭ), осуществляющий дискретизацию по времени и модуляцию. В схемах импульсный элемент обозначают так, как показано на риc. 2.
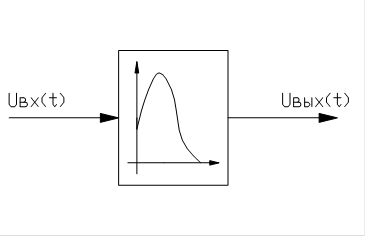
Рис. 2 Таким образом, импульсный элемент порождает последовательность импульсов, параметры которых связаны со значениями непрерывного сигнала в моменты квантования 0, Т,2Т,3Т (здесь и далее будем считать моменты квантования равностоящими друг от друга). В зависимости от того, какой параметр импульса определяется значениями выделенных дискрет, различают амплитудно-импульсную, широтно-импульсную и фазо-импульсную модуляции. В случае амплитудно-импульсной модуляции амплитуда импульса постоянной длительности An определяется дискретой f[nT]
В частном случае линейной амплитудно-импулъсной модуляции
Этот случай иллюстрируется рис. 3,а.
Рис. 3 При широтно-импульсной модуляции (рис. 3,б) амплитуда импульсов постоянна, а их длительность (не превышающая интервала квантования) зависит от выделенных значений дискрет, т.е.
Рис. 4
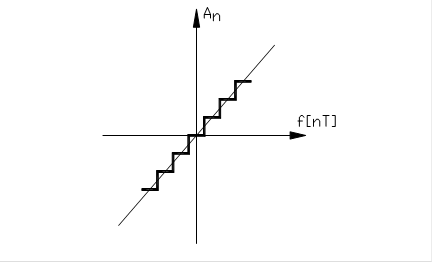
При фазо-импульсной модуляции амплитуда и ширина импульса постоянны, а величина f[nT] определяет его положение внутри интервала квантования (рис.3,в), т.е.
Отметим, что два последних вида импульсной модуляции принципиально нелинейны. Дискретизацию и по времени и по уровню можно рассматривать как амплитудно-импульсную модуляцию, когда в зависимости для An функция Линейные импульсные системы характеризуются наличием в своем составе импульсного элемента, осуществляющего линейную амплитудно-импульсную модуляцию.
Лекция 2 Предварительные замечания Как и в непрерывных системах, исследование динамики дискретных систем может проводиться либо с использованием переменных состояния, либо с использованием входных и выходных переменных систем. В первом случае исследование обычно проводят во временной области, рассматривая систему разностных уравнений и анализируя свойства ее решений. Этот подход и разработанные в его рамках методы являются весьма плодотворными. Они позволяют рассматривать нелинейные многомерные дискретные системы, проводить исчерпывающее исследование их свойств, решать задачи синтеза в различной постановке. Во втором случае исследуют не весь набор переменных состояния, а лишь поведение некоторых величин, по изменению которых и оценивается качество САУ - выходные переменные системы. В задачу исследования может входить анализ зависимости выходных переменных от входных величин, решение вопроса, как придать системе требуемые свойства по этим переменным и т.п. При этом для линейных импульсных систем наиболее простым и распространенным математическим аппаратом описания и исследования является аппарат дискретного преобразования Лапласа и Z -преобразования, позволяющий получить уравнение САУ в изображениях и найти дискретные передаточные функции. Рассмотрим вопросы описания и исследования дискретных систем каждым из указанных методов. Начнем со второго подхода, когда для математического описания системы используются уравнения в изображениях и дискретные передаточные функции.
Лекция 3
Уравнения и передаточные функции разомкнутых импульсных систем.
План лекции: 1. Эквивалентная схема разомкнутой импульсной системы. 2. Уравнения разомкнутой импульсной системы. 3. Передаточная функция разомкнутой импульсной системы.
Лекция 4 Пример вычисления Z –передаточной функции. Найдем Z-передаточную функцию разомкнутой системы, состоящей из ИЭ с экстраполятором нулевого порядка и непрерывной части с передаточной функцией Передаточная функция ПНЧ имеет вид
Для нахождения W(z) применим формулу (23):
Полюсы выражения Тогда получим
Отсюда следует
Этот же результат можно получить с помощью таблицы
Проводя разложение на простейшие дроби, найдем
Отметим некоторые свойства Z-передаточных функций. Передаточная функция есть дробно-рациональная функция z. При использовании модифицированного Z-преобразования числитель этой функции зависит от e. Порядком передаточной функции
Полюсы
Рассмотрим задачу определения реакции дискретной системы с передаточной функцией
Таким образом, если Z-преобразование выходной величины известно, процесс на выходе может быть найден по формуле обратного Z-преобразования:
Для нахождения
где Для вычисления обратного Z-преобразования, кроме того, может быть использовано разложение изображения в ряд Лорана [4]. Наконец, по известной Z-передаточной функции нетрудно составить соответствующее разностное уравнение импульсной системы. Пусть
Тогда уравнение (25) можно переписать в виде
Переходя к оригиналам и учитывая теорему о смещении аргумента решетчатой функции, получим
Это соотношение представляет собой разностное уравнение системы, с помощью которого можно рассчитать процесс на выходе дискретной САУ. Лекция 5 Лекция 6
Лекция 7 Лекция 8 Лекция 9 Понятие устойчивости. Анализ устойчивости является необходимым этапом исследования любой системы автоматического управления, так как именно это свойство в решающей степени определяет принципиальную возможность практического использования САУ. Основные понятия теории устойчивости непрерывных систем рассматривались в курсах "Математические основы ТАУ" и "Основы ТАУ". Будем считать, что линейная импульсная система устойчива тогда и только тогда, когда ее реакция на любое ограниченное воздействие ограничена. Соответственно, если найдется хотя бы одно ограниченное внешнее воздействие, реакция системы на которое не будет ограничено, то такая импульсная система называется неустойчивой.
Лекция 10 Критерий Шура-Кона. Для оценки устойчивости может использоваться также алгебраический критерий Шура - Кона. Рассмотрим характеристическое уравнение (50) и составим из его элементов следующую последовательность матриц:
Составим из матриц
Для обеспечения устойчивости импульсной системы с характеристическим уравнением (50) необходимо и достаточно, чтобы число перемен знака в последовательности
было равно n, т.е. степени характеристического уравнения. Иначе, должно выполняться условие:
Особенностью использования критерия Шура - Кона и его существенным неудобством является необходимость вычисления определителей высокого порядка. Рассмотрим пример применения критерия Шура – Кона для исследования устойчивости импульсной системы. Пусть характеристическое уравнение системы имеет вид:
Составляем последовательно:
Используя критерий Шура-Кона, можно заключить, что система с данным характеристическим уравнением устойчива. Лекция 11 Аналог критерия Михайлова. Частотные критерии устойчивости удобно применять к системам высокого порядка. Одним из распространенных критериев устойчивости непрерывных систем является критерий Михайлова. Для импульсных систем можно сформулировать аналог этого критерия. Пусть характеристическое уравнение замкнутой импульсной системы имеет вид
В соответствии с принципом аргумента [3] число корней характеристического многочлена, лежащих внутри единичной окружности, равно числу полных оборотов вектора
Очевидно, что если m = n, то все корни
и система устойчива. Наибольшую сложность при использовании этого критерия представляет нахождение отображения единичной окружности на плоскости B. При этом рассматривать многочлен B(z) в функции z неудобно, так как аргумент z меняется сложным образом. Проще перейти к переменной
Таким образом, рассматривается функция
то годограф Примеры годографов, соответствующих устойчивым системам при n =1,2, 3, показаны на рис.25.
Рис.25.
Лекция 12 Лекция 13 Лекция 15 Лекция 16 Лекция 17 Пример составления математического описания импульсной системы. Рассмотрим более подробно математическое описание подобных систем на примере. Пусть структурная схема дискретной системы имеет вид, представленный на рис.39,а. Данная система является асинхронной. Периоды повторения первого ИЭ Т и второго кратные числа, причем T=2T1. Формирующие звенья обоих импульсных элементов представляют собой экстраполяторы нулевого порядка. Временная диаграмма работы импульсных элементов представлена на рис.39.б. Примем за переменные состояния координаты x1,x2. Входное воздействие u(t) будем считать непрерывной функцией. Рассмотрим временной интервал (kT,t1) и запишем дифференциальные уравнения, соответствующие переходу
Рис. 39 Решив данную систему, получим при
Подставим
Представим систему в виде
Рассмотрим далее дискретный переход
т.е.
где
Объединив результаты двух рассмотренных переходов, получим
или
так как для данного случая Рассмотрим следующий временной интервал
Решив данную систему, получим при
При t=(k+1)T имеем
или, переходя к матричной форме записи,
где
Дискретный переход
Объединив выражения (83), (85). (86), получим
Подставляя в зависимость (87) выражение для
или
где
Таким образом, получена система разностных уравнений (88), определяющая связь между значениями переменных состояния на интервале основного квантования Т. Устойчивость рассматриваемой дискретной системы определяется собственными числами матрицы Ф. Полученные зависимости позволяют провести расчет переходных процессов в данной системе. Лекция 18 Лекция 19 Лекция 20
Лекция 21 Пример синтеза последовательного аналогового корректирующего устройства. Пусть неизменяемая часть системы имеет передаточную функцию
Тогда Z-передаточная функция разомкнутой САУ имеет вид
Применяя W-преобразование получим
Соответствующие ЛАФПЧХ изображены на рисунке 48.
рис.48 Фазовая характеристика пересекает уровень -180 при l=1 и САУ имеет малые запасы устойчивости. Чтобы получить Dj =450 частоту среза нужно сдвинуть в точку l=0.4, где
Считая, что частота l=0,4 будет находиться на высокочастотных асимптотах числителя и знаменателя, определим 20lg и тогда
Чтобы отрицательный фазовый сдвиг, вносимый регулятором, незначительно влиял на ФЧХ в окрестности новой частоты среза значение 1/
Тогда W-передаточная функция D*(w) примет вид
Таким образом
Z-передаточная функция разомкнутой системы имеет вид
Переходная функция скорректированной САУ представлена на рис.49. Качество переходных процессов в скорректированной системе является хорошим.
рис. 49 Определим ПФ аналогового регулятора. Имеем
причем, учитывая, что в таблицах преобразований всегда присутствует член (1-Tw/2), необходимо раскладывать на элементарные дроби выражение
Каждому слагаемому правой части последнего выражения по таблице подбираем пару
и тогда
откуда
Чтобы D(p) была физически реализуема добавим удаленный полюс р=-10. В итоге получим:
Лекция 22 Лекция 23 Общие положения.
Рассмотренные способы синтеза базировались на основе непрерывных систем, использующих ЛАФЧХ, регуляторы с опережением или отставанием по фазе. Однако структура ЦР отличается большой гибкостью, поэтому можно разработать оригинальные методы, отличные от метода синтеза непрерывных САУ. Большая часть СУ проектируется так, чтобы переходный процесс в них возможно быстрее достигал требуемого значения. Этот класс систем называется системами с минимальным временем переходных процессов или системами оптимальными по быстродействию. Решение задач синтеза ЦСУ с минимальным временем ПП рассматривается далее.
Пример.
Рассмотрим пример:
Пусть последовательный цифровой регулятор имеет ПФ
Тогда ПФ разомкнутой скорректированой системы
То есть введение КУ приводит к компенсации всех нулей и полюсов исходной системы и появлению нового полюса Z=1 Соответствующая ПФ замкнутой системы:
Тогда при ступенчатом входном сигнале
Это означает, что выходной сигнал у[kT] достигает требуемого значения за один период квантования и с этого момента сохраняет требуемое значение. Перерегулирование нулевое. Однако в общем случае, хотя у(кТ) может иметь малое перерегулирование, действительная реакция у(t) может сопровождаться импульсами. Так как Т<< постоянных времени объекта, можно ожидать, что y[kT] достаточно хорошо совпадает с y(t). Поэтому можно ожидать, что переходная функция достигает установившегося значения через Т=0.1с, а между моментами квантования пульсаций не будет или они будут малы. Такой тип реакции называется апереиодическим переходным процессом. Апериодический переходный процесс можно получить только в случае, когда есть полная компенсация нулей и полюсов. На практике реальное ограничение приводит к тому, что достичь идеального апериодического процесса невозможно.
Рис. 54.
Что должно быть в результате синтеза: 1. Нулевая установившаяся ошибка при определении входного сигнала. 2. Длительность переходного процесса должна быть минимальной 3. Цифровой регулятор должен быть физически реализуемым
ПФ замкнутой скорректированной системы имеет вид:
откуда
при этом
Будем рассматривать класс входных сигналов, изображение которых имеет вид:
где N-натуральное число A(z)- многочлен от z В общем случае выражение (*) соответствует входному сигналу типа
Например, при
С учетом (*), используя теорему определьном значении найдем установившуюся ошибку
Исходя из полученного выражения выясним, что необходимо, чтобы Еуст=0. Так как А(1)<>0,то очевидно, что для этого 1-Ф(z) должно содержать скобку
где R(z)-полином от Z Следствием того, что 1-Ф(z) представимо в форме (6) будет выражение:
Полюсы Ф(z) могут возникать как: — нули знаменателя Z=0 — полюсы числителя, так как R(z)-многочлен от Z, то это может быть только Z=0 Таким образом, при сделанных предложениях, Ф(z) имеет единственный полюс Z=0. Характеристическое уравнение имеет вид:
Подставив (6) и (4) в (3) получим E(z)=A(z)R(z) — это Z-преобразование ошибки. При этом, так как A(z) и R(z) -полиномы от Z, то E(z) тоже полином от Z и следовательно E(z) имеет конечное число членов при разложении в ряд по степеням Z. Таким образом, пр исделанных предложениях сигнал ошибки сводится к нулю за конечное число периодов квантования. Таким образом, синтез цифрового регулятора может проводиться так R(z)®Ф(z)®D(z) При этом необходимо иметь физически реализуемую ПФ. Это можно проконтролировать при выборе Ф(z)
разность степеней числителя и знаменателя не меньше, чем у W(z), это необходимо учитывать при определении Ф(z). Вернемся к соотношению(6). N определяется типом входного сигнала. Тогда N ступенчатый сигнал 1
линейный 2
парабола 3
Видно, что при этом для ступенчатого сигнала минимальное время установления е=0 составляет один такт, для линейного — 2 такта и т.д. Рассмотренный алгоритм определения D(z) имеет ряд особенностей: 1. Если W(z) имеет нули на единичной окружности или вне ее, то будет нужен енустойчивый регулятор. Этот случай нужно рассматривать отдельно 2. В таблице m=1 и должно быть, чтобы m<=1 Таким образом: если есть такие нули или m>1, то R(z) не может быть 1
Пример: Пусть
Нельзя взять Ф(z)=1/z из таблицы Попробуем взять
При этом
и процесс заканчивается за два такта. В общем случае при заданном входе, определяющем N, минимальное число переиодов квантования, составляющих переходный процесс, равно N+m-1 Лекция 24 Общие положения.
Задача реализации аналогового прототипа цифровым фильтром может встретиться при построении непрерывной системы, если корректирующее устройство слишком сложно и трудно реализуется на аналоговых элементах. В этом случае его заменяют эквивалентным цифровым корректирующим устройством. Кроме того, благодаря чисто конструктивным и эксплуатационным преимуществам может оказаться оправданным перевод на цифровое управление уже имеющихся непрерывных систем. И, наконец, возможен вариант, когда систему синтезируют как непрерывную, заранее зная, что корректирующее устройство будет реализовываться в цифровом виде. Tакой подход можно оправдать тем, что аппарат синтеза непрерывных САУ более развит, чем аппарат синтеза дискретных систем. Следует отметить, что этот подход в общем случае малоперспективен, так как при этом заведомо нельзя получить результаты лучше, чем в непрерывном варианте.
Пример нахождения цифрового фильтра, соответствующего данному прототипу.
Пример. Пусть
Найдем цифровой фильтр, соответствующий данному прототипу. Имеем
Используя соответствие (115), получим
или
где T - период дискретности цифрового фильтра. Лекция 25 Обзор задач динамики.
Одной из основных задач динамики механических систем является задача определения управляющих сил по заданным свойствам движения. Задачи такого рода с различными их видоизменениями называют обратными задачами динамики. Обратные задачи динамики всегда привлекали к себе внимание, так как имеют широкие прикладные возможности. Из возможных постановок обратных задач динамики рассмотрим задачу аналитического построения программного движения. При этом необходимо построить такую физическую систему, чтобы процессы в ней удовлетворяли заранее заданным свойствам. Назовем заданные свойства процесса программой движения, а весь процесс - программным движением рассматриваемой системы. В конечном счете программное движение осуществляется действием на систему управляющих сил. Построение уравнений движения управляющих устройств составляет задачу аналитического построения замкнутых систем программного движения. При этом в задачу аналитического построения систем программного движения включаются как задачи установления осуществимости самой программы, так и задачи обеспечения устойчивости движения при наличии начальных отклонений переменных системы от их заданных значений.
Лекции по курсу «Системы цифрового управления»
Лекция 1 Общие сведения о дискретных автоматических системах План лекции 1. Квантование по времени и по уровню. 2. Виды импульсной модуляции. 3. Импульсные и цифровые методы в системах автоматического управления (САУ).
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.239.46 (0.25 с.) |
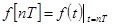
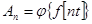 .
.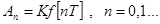 .
.
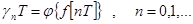 .
.
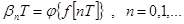 .
.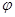 имеет вид, представленный на рис. 4. Таким образом, цифровые системы можно трактовать как один из типов нелинейных импульсных систем.
имеет вид, представленный на рис. 4. Таким образом, цифровые системы можно трактовать как один из типов нелинейных импульсных систем.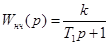 .
.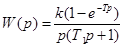 .
. .
. следующие:
следующие: 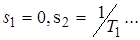 .
.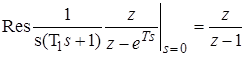 ;
; 
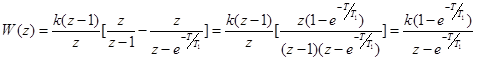
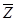 -преобразования, а именно
-преобразования, а именно .
.
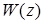 назовем степень n ее знаменателя. Порядок дискретной передаточной функции равен степени знаменателя передаточной функции непрерывной части системы
назовем степень n ее знаменателя. Порядок дискретной передаточной функции равен степени знаменателя передаточной функции непрерывной части системы  .
.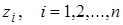 Z-передаточных функций
Z-передаточных функций 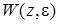 связаны с полюсами
связаны с полюсами 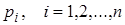 передаточной функции
передаточной функции 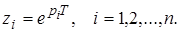 (24)
(24)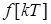 . Определив Z-преобразование входного сигнала
. Определив Z-преобразование входного сигнала  , запишем уравнение системы в изображениях:
, запишем уравнение системы в изображениях: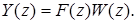 (25)
(25)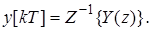
 можно применить известную формулу
можно применить известную формулу
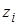 - полюсы функций
- полюсы функций 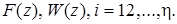
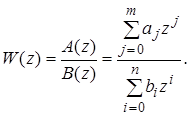


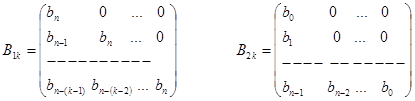
 и
и  матрицу
матрицу  размерности (2k´2k)
размерности (2k´2k) , k=1,2,…,n.
, k=1,2,…,n.
 для нечетных k;
для нечетных k; для четных k.
для четных k. .
.

 ,
, ,
, ,
, 

 0,2841,
0,2841,



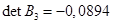
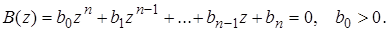
 при обходе точкой z единичной окружности, т.е.
при обходе точкой z единичной окружности, т.е. .
. удовлетворяют соотношению
удовлетворяют соотношению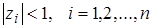
 по формуле
по формуле  . При этом движению точки z по единичной окружности соответствует изменение
. При этом движению точки z по единичной окружности соответствует изменение 
 и строится ее годограф в пределах
и строится ее годограф в пределах  ,
,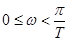 . При этом приращение аргумента функции
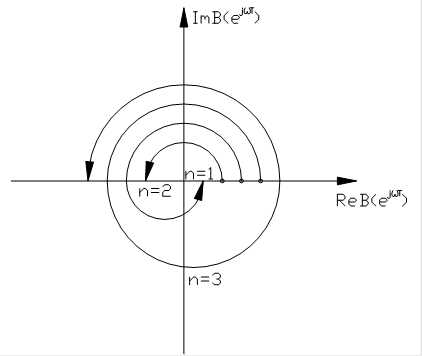
. При этом приращение аргумента функции  ;
; 




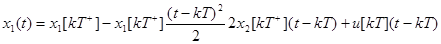

 найдем
найдем



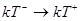
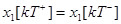

 (83)
(83) .
.
 (84)
(84) .
. Запишем дифференциальные уравнения, соответствующие переходу
Запишем дифференциальные уравнения, соответствующие переходу 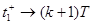 . При этом следует иметь в виду, что в момент времени t1 срабатывает только второй ИЭ, а выходной сигнал первого ИЭ не меняется. Уравнения имеют вид
. При этом следует иметь в виду, что в момент времени t1 срабатывает только второй ИЭ, а выходной сигнал первого ИЭ не меняется. Уравнения имеют вид



 и тогда
и тогда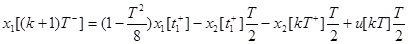

 (85)
(85)
 аналогичен рассмотренному дискретному переходу
аналогичен рассмотренному дискретному переходу  (86)
(86) (87)
(87) , будем иметь
, будем иметь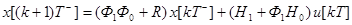
 (88)
(88)
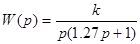 .
.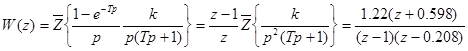
 .
.
 . Для этого АЧХ в окрестности l=0,4 нужно опустить на 8 дб без уменьшения коэффициента передачи системы. Выберем в качестве аналогового регулятора D*(w) модель с передаточной функцией:
. Для этого АЧХ в окрестности l=0,4 нужно опустить на 8 дб без уменьшения коэффициента передачи системы. Выберем в качестве аналогового регулятора D*(w) модель с передаточной функцией: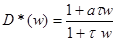 (
( ).
). из условия требуемого ослабления:
из условия требуемого ослабления:
 .
.
 .
.


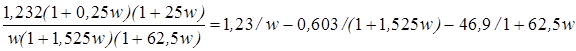 .
.
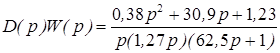
 .
. .
.





 (1)
(1)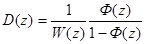 (2)
(2) (3)
(3) (4)
(4)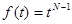
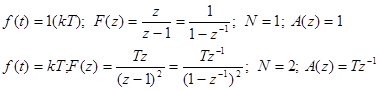
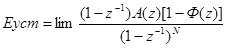 (5)
(5) т.е.
т.е. (6)
(6)







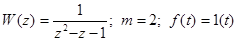
 , тогда
, тогда
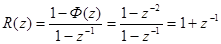
 .
. .
.
 ,
,


