
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Передаточная функция параллельного соединения звеньев равна сумме передаточных функций отдельных звеньевСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
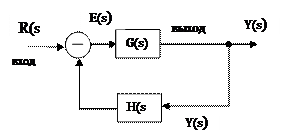
Передаточная функция замкнутой системы с обратной связью Передаточная функция замкнутой системы с отрицательной обратной связью.
b(s)
Y(s)=E(s)*G(s)
Передаточная функция замкнутой системы с отрицательной обратной связью равна передаточной функции объекта управления, поделенной на произведение передаточных функций объекта управления и управляющего устройства(передаточной функцией разомкнутой системы), сложенного с единицей. Можно заметить, что система будет хорошо отслеживать входной сигнал R(s), когда Тогда Те же соображения позволяют определить как подавить возмущения, действующие на систему. Необходимо сделать передаточную функцию системы по возмущению Характеристическое уравнение замкнутой системы Знаменатель передаточной функции замкнутой системы представляет собой характеристическое уравнение замкнутой системы. Именно знак действительной части корней этого уравнения определяет устойчивость замкнутой системы с регулятором 1+H(s) G(s) =0
Для примера из лекции7 и лабораторных работ Линеаризованное описание отклонения ракеты по угловому положению от заданного, например, по каналу тангажа и описание поведения управляющего устройства, имеет вид:
τ
Здесь υ- отклонения угла тангажа от заданного положения δ - отклонение управляющего органа (управляющего двигателя ракеты) Формально передаточная функция получается из дифференциального уравнения после замены в нем символов кратного дифференцирования на соответствующую степень s и деления образованного таким образом многочлена правой части уравнения на многочлен левой части уравнения. Дифференциальное уравнение получается из передаточной функции путем обратной замены степеней s на символы кратного дифференцирования. Передаточная функция автомата стабилизации- управляющего устройства.
Wyy(s) = (a0 +a1 s) Wио = (a0 +a1 s)/(τ s +1)
Передаточная функция объекта управления W0 (s) = Cυδ /(s2 +Cυυ)
Передаточная функция замкнутой системы Wзам.сист = (a0 +a1 s) Cυδ // ((a0 +a1 s) Cυδ + (s2 +Cυυ) (τ s +1))
Тогда характеристическое уравнение (s2 +Cυυ) (τ s +1) + Cυδ (a0 +a1 s) = 0 τs3 + Cυυ τ s + s2 + Cυυ + Cυδ a0 + Cυδ a1 s =0
Это характеристическое уравнение третьего порядка. Необходимое, но недостаточное условие устойчивости – все коэффициенты характеристического уравнения должны иметь один знак. Так как С С Если ракета статически устойчива, то значение коэффициента Cυυ >0, если статически неусточива, то Cυυ <0. Представляя Достаточное условие устойчивости (критерий Гурвица) для характеристического уравнения третьего порядка приводит к соотношению Cυυ τ + Cυδ a1 - τ(Cυυ + Cυδ a0)≥ 0, раскрывая скобки Cυδ a1 - τ Cυδ a0 ≥ 0 или T Это условие совпадает с предыдущим. Таким образом, для статически неустойчивой ракеты значение коэффициента усиления автомата стабилизации должно быть больше значения a0>(- Cυυ/ / Cυδ) и T В противном случае угловое движение ракеты будет неустойчивым. Запас по реальному значению коэффициента усиления a0 должен быть примерно в два три раза больше граничного значения, определенного по приведенному выражению, что по опыту обеспечит приемлемое качество переходных процессов. Значения коэффициентов уравнения углового движения ракеты принимались постоянными и равными Сυυ = - 0,6 1/сек2 (ракета статически неустойчива – центр давления ближе к носу ракеты, чем центр масс) Сυδ = 1 1/сек2 Мв = 0,2 1/сек2 Дифференциальное уравнение, описывающее изменение по времени управляемой координаты υ(t), полученное из передаточной функции
Собственный период колебаний ракеты с АС
T=2π/ωc ωс = Частотные методы исследования систем управления ТС
До сих пор для исследования систем автоматического управления используются частотные методы, частотные амплитудно-фазовые характеристики систем. Появившиеся в докомпьютерную эру, когда непосредственное нахождение корней характеристического уравнения или интегрирование уравнений движения системы представляло техническую проблему, частотные методы сохранили своё значение до настоящего времени. Если на вход системы подать периодическое входное воздействие u= A sin ωt, где А и ω- соответственно постоянная амплитуда и частота, то на выходе устойчивой линейной системы установится выходная функция Y=B sin (ωt+β) Отношение В/А зависит от частоты и, как функция частоты ω, называется амплитудной частотной характеристикой системы и зависит от динамических её свойств, определяемых уравнениями математической модели системы и значениями их параметров. То же самое можно сказать о сдвиге фазы колебаний Ф(ω), называемой фазовой частотной характеристикой. Относительно свойств амплитудно - частотной и фазо-частотной характеристик в теории управления были развиты методы, позволяющие сделать суждения об устойчивости системы и о качестве переходных процессов в ней по их виду. Например критерий устойчивости Найквиста позволяет сделать заключение, об устойчивости замкнутой системы по прохождению годографа частотной характеристики разомкнутой системы относительно точки1,0. Вычисление амплитудно - частотной и фазо-частотной характеристик может быть проведено численно по передаточной функции системы W(s). Достаточно вместо комплексного числа s подставить в выражение для передаточной функции его чисто мнимое значение iω. S=iω. Модуль полученного после соответствующих преобразований комплексного числа, как функция ω, и будет амплитудно- частотной характеристико системы. А(ω) = Фаза полученного комплексного числа – фазовая частотная характеристика Φ(ω) = arctg (Q(ω) /D(ω)) Здесь Q(ω), D(ω) – соответственно мнимая и действительные части комплексного числа W(iω). Частотные характеристики могут быть получены также и экспериментальным образом непосредственно с реальных устройств системы управления путем подачи на их вход гармонических сигналов также с физических генераторов этих сигналов и записи реакции реальных устройств на эти сигналы. В этом случае можно даже обойтись без составления математической модели данных устройств при исследовании системы управления. Это пожалуй и является основной причиной того, что достаточно древние частотные методы исследования систем до сих пор применяются, несмотря на то, что прямое численное решение уравнений математической модели позволяет быстро ответить на все возникающие вопросы в том числе по качеству процессов управления. Мы в дальнейшем в нашем курсе частотные методы не рассматриваем, опираясь в основном на исследования корней характеристического уравнения и на численное интегрирование уравнений математической модели.
Математические модели СТС и запаздывания и упреждения при управлении
Динамику поведения системы управления технической системой можно описать любым из трех принятых в теории управления способов, которые мы рассмотрели: 1. в виде одного дифференциального либо разностного уравнения, связывающего вход системы с интересующим выходом системы, 2. в виде передаточной функции (для линейных систем), делающей то же самое, но в несколько более наглядном виде, 3. в виде системы дифференциальных либо разностных уравнений первого порядка относительно переменных состояния. 4. В виде частотных характеристик системы. Переход между этими описаниями взаимно однозначный. Каждое их них обладает удобствами для определенных целей. Нами первоначально рассматривалось базовое описание динамики системы дифференциальным уравнением. В первых двух видах представления соответственно левая часть ДУ и знаменатель передаточной функции определяют запаздывание вследствие инерционности той или иной физической природы, приводящей в некоторых случаях к колебательному поведению системы, а в некоторых случаях и к потере ею устойчивости. Правая часть дифференциального уравнения и числитель передаточной функции наоборот вносят «опережение» в динамику, компенсирующее в той или иной мере «запаздывание», определяемое соответственно левой частью дифференциального уравнения и знаменателя передаточной функции.
Лекция 5. Управление в условиях неопределенности, Адаптивное управление и управление с обучением. Универсальная природа основных особенностей цифрового управления. Управление в условиях неопределенности. Случайные возмущения и параметры системы. В некоторых задачах управления вопрос управления ставится так, что модель объекта управления и действующих возмущений не определена с необходимой точностью на стадии проектирования. Иногда параметры объекта управления или регулятора являются или принимаются случайными и случайным образом меняются в некотором диапазоне. Возможен учет этих случайных разбросов параметров и возмущений, принимая их значения предельными. При этом при таком подходе возможны ситуации, когда невозможно создать регулятор, обеспечивающий приемлемое качество управления во всем диапазоне разбросов параметров объекта управления. Пусть имеется ряд действующих на объект управления возмущений. Эти возмущения являются следствием ряда независимых и случайных причин: конструктивных разбросов, ошибок изготовления, разбросов температуры, разбросов питающего напряжения и т.п. Пусть эти возмущения имеют значения, не превышающие с большой вероятностью величину εi. Учитывая случайный и независимый характер этих возмущений суммирование их нужно проводить по правилам суммирования случайных чисел, которые нам даёт теория вероятностей. Математическое ожидание суммы независимых случайных возмущений равно сумме их математических ожиданий. Дисперсия суммы независимых случайных возмущений ошибок равна сумме их дисперсий. Поэтому Предельное отклонение или предельная случайная ошибка относительно математического ожидания возмущения с большой вероятностью εпред=3σ. (Для нормального закона с вероятностью 0,997).
Адаптивное управление. Другой подход к управлению, обеспечивающий достижение необходимых характеристик качества управление такими техническими системами, опирается на методы адаптивного управления. Адаптивное управление это управление, при котором управляющие воздействия вырабатываются при заранее неизвестных или изменяющихся в процессе эксплуатации свойствах системы управления. Как правило, адаптация достигается посредством формирования в явном или неявном виде математической модели процессов системы управления (в управляющем компьютере) при её работе. Отметим, что на формирование этой модели требуется какое - то время. Адаптивное управление меняет параметры регулятора или структуру регулятора в зависимости от изменения параметров объекта управления или возмущений, действующих на объект управления и на структурные элементы управляющих устройств. По характеру изменений в управляющем устройстве адаптивные системы делятся на самонастраивающиеся, изменяющие параметры регулятора, и на самоорганизующиеся, изменяющие структуру регулятора. Адаптивные системы с эталонной моделью содержат в своем составе (в ПО управляющей ЦВМ) математическую модель системы, обладающую требуемым качеством реакций на управляющие и возмущающие воздействия. Адаптивные модели с идентификатором проводят сначала идентификацию параметров объекта управления, а затем определяют настройки регулятора и их подстройку таким образом, чтобы реакция системы на входные воздействия соответствовала бы реакции системы с эталонной моделью. Все это производится в управляющей ЦВМ соответствующим ПО. Для прикладных задач, связанных с управлением технологическими процессами в общем случае необходимо построение математической модели процесса. Это позволяет подобрать по данной модели параметры регулятора. Однако, часто в таких случаях построение строгой и формальной математической модели затруднительно, так как идентификация параметров таких чаще всего нелинейных моделей, меняющихся в широком диапазоне, требует большого времени, сложна и не может быть проведена заранее - при проектировании системы. Применение «нечеткого управления» в этих случаях позволяет обойти эти трудности. Достаточно сформулировать правила поведения регулятора в форме нечетких суждений. Нечеткие регуляторы применяются также в случаях когда управление требует участия эксперта, который на основании своего опыта достаточно хорошо управляет подобными сложными объектами, руководствуясь показаниями приборов и некоторыми эвристическими правилами, которые не полностью формализованы и могут быть отнесены к нечетким. Для управления в ситуациях подобной неопределенности также используются нейронные сети, а также генетические алгоритмы. Это все названия соответствующих компьютерных технологий. Длительность обучения нейронной сети это основной недостаток данной компьютерной технологии. Другой недостаток – невозможность предсказать ошибки управления при входных воздействиях, на которых система не обучалась, а такие ситуации в реальных системах вполне возможны. Не исследована робастность подобных систем. Генетические алгоритмы основаны на принципах естественного отбора. Недостаток тот же самый - большое время поиска оптимальных настроек регулятора, часто превышающее время самого процесса управления. Это не позволяет широко использовать эти компьютерные технологии в системах реального времени. Универсальная природа основных особенностей цифрового управления в автоматических и автоматизированных системах. Квантование по времени.
Рассмотрим на рисунке эти три фазы управления от ЦВМ. За время фазы ненаблюдаемости и неуправляемости фазовые координаты объекта управления меняются под действием возмущений и начальных условий на момент начала неуправляемости. Поэтому выдаваемое в конце третьей фазы управляющее воздействие рассчитано по устаревшей информации и уже не соответствует состоянию объекта управления на момент его выдачи t3, а соответствует состоянию на момент t1. Поэтому выработанное управляющее воздействие не приведет объект управления в желаемое состояние. Поэтому цикл управления надо повторить, но описанная картина повторится. И так до бесконечности пока система работает. Поэтому в цифровых системах управления циклы управления повторяются, т.е. ЦВМ решает набор задач управления с определенным периодом в течение всего времени работы системы. Это - универсальная особенность работы цифровых автоматизированных и автоматических систем любого назначения. Например, она прослеживается и в системе управления самолетом от БЦВМ и в системе управления кадрами предприятия, когда сводку о наличном составе кадров необходимо готовить по крайней мере раз в день для расчета бухгалтерией зарплаты. С каким периодом надо повторять решение задач управления? Период повторения решения зависит от временных характеристик действующих возмущений и динамики системы при их отработке. Т.е. не наблюдаемые в течении периода дискретизации изменения управляемых координат должны быть достаточно малы. Чем меньше период повторения решения задачи управления, тем меньше негативный эффект дискретности управления, связанный с внесением запаздывания. Для нас важно то, что в период повторения решения задачи входит не только время её распределенного решения в управляющих компьютерах сети, но и время передачи обработанной в компьютерах информации между ними. Это время ограничивается периодом решения и должно быть небольшим т.е. скорость передачи информации по сети должна быть высокой.Имеющиеся на нашей диаграмме окна в реальных системах не уничтожаются, а наоборот расширяются для многозадачной работы.
Квантование по уровню в цифровых СУ. Второй эффект квантования связан с тем, что представление данных в компьютере происходит в ограниченной разрядной сетке (16, 32, 64 разряда). Чем выше разрядность компьютера, тем точнее представлены данные. Однако, доступная разрядность данных определяется уровнем развития микроэлектроники. Этот эффект начинается с АЦП, который имея ограниченное число разрядов преобразует аналоговый сигнал с погрешностью в цену половины младшего разряда. Далее идут интересные факты уже при машинном счете. Имеет место свойство цифровых вычислительных машин (ЦВМ) – округление арифметических операций, так как результат, например умножения, двух 32-разрядных чисел занимает 64 разряда. Арифметическое устройство 32-разрядной машины позволяет разместить эти 64 разряда в сумматоре, но далее его надо переписать в память или регистр, а они 32-разрядные. Поэтому, результат при пересылке в память или регистры ЦВМ округляется. Младшие разряды отбрасываются вплоть до 32 разрядов. При этом, если старший из отбрасываемых разрядов 1, то в младший оставшийся добавляют 1; если 0, то ничего не добавляется. Т.е. возникает погрешность с математическим округлением младшего разряда на каждой операции. Каждая последующая операция уже над полученными неточными числами увеличивают эту погрешность.
Эта погрешность захватывает все большее и большее число младших разрядов результата. Это может продолжаться до тех пор, пока ошибка вычисления конечного результата превышает допустимый по точности решения задачи уровень. Выход из данной ситуации – использовать ЦВМ с большей длиной разрядной сетки либо использовать имеющийся во многих архитектурах ЦВМ операции с двойной длинной операндов и результатов. В последнем случае эти операции выполняются на программно-аппаратном уровне, и потому очень сильно, на порядок и более, снижают быстродействие ЦВМ, но зато повышается точность представления результатов. Как говорят, точность разменивается на время. В программировании это можно сделать всегда. Надо отметить, что эффект нехватки точности из-за разрядной сетки в цифровых системах управления (САУ) характерен для ограниченного числа вычислительных задач с длительным формульным счетом. Для большинства задач управления этот эффект мало заметен и маскируется точностью АЦП при вводе данных с аппаратуры и частым их обновлением. Тем не менее, использование ЦВМ с максимально доступным числом разрядов данных уменьшает все проблемы точности вычислений. Именно поэтому как только позволяет технология микроэлектроники, так формат данных удваивается. При относительно малых дискретности работы управляющей ЦВМ эффект квантования по времени сводится в первом приближении к внесению в контур управления чистого запаздывания, равного половине периода квантования. При этом нелинейными эффектами, связанными с квантованием по уровню обычно пренебрегают из-за их малости. Вопросы для повторения Управление в условиях неопределенности, адаптивное управление, управление с обучением Универсальная природа основных особенностей цифрового управления в автоматических и автоматизированных системах. Квантование по времени. Квантование по уровню в цифровых СУ.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.116 (0.052 с.) |

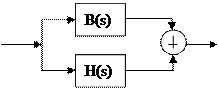
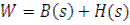
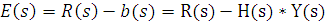
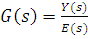
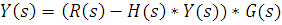
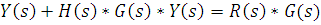
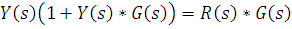
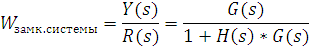
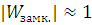 ; это означает, что круговой коэффициент усиления системы
; это означает, что круговой коэффициент усиления системы 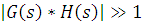 и
и 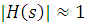
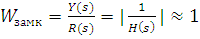
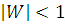 , при этом
, при этом 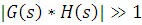 и
и 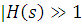 .
.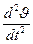 + Сυυ υ + Сυδ δ = Мв
+ Сυυ υ + Сυδ δ = Мв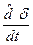 + δ = а0 υ + а1
+ δ = а0 υ + а1 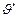
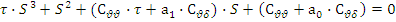
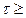 0, то
0, то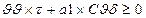

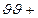 a0
a0 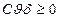
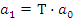 , имеем Т –постоянную времени дифференцирования
, имеем Т –постоянную времени дифференцирования 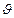 . Для устойчивости надо, чтобы T
. Для устойчивости надо, чтобы T 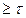 Что можно интерпретировать, как необходимость внесения в систему упреждения большего, чем имеющееся в ней запаздывание.
Что можно интерпретировать, как необходимость внесения в систему упреждения большего, чем имеющееся в ней запаздывание.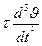 +
+ 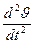 + (Cυυ τ + Cυδ a1)
+ (Cυυ τ + Cυδ a1) 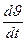 + (Cυυ + Cυδ a0)
+ (Cυυ + Cυδ a0) 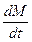
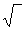 (Cυυ + Cυδ a0)
(Cυυ + Cυδ a0)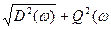 )
) 
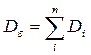 .Тогда среднеквадратичное отклонение суммы случайных возмущений от их математического ожидакния
.Тогда среднеквадратичное отклонение суммы случайных возмущений от их математического ожидакния 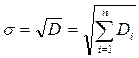
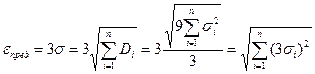 или εпред =
или εпред = 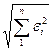 <
< 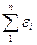
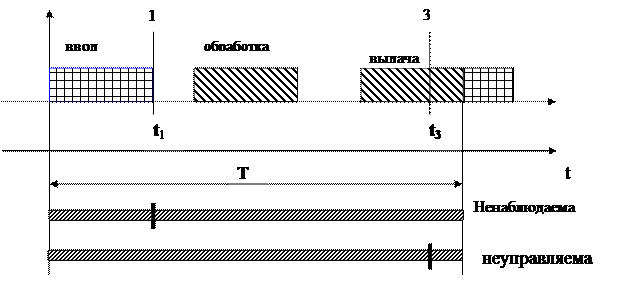 После ввода информации с чувствительных элементов (ЧЭ) в ЦВМ, она производит ее обработку, на которую уходит какое-то время. После чего на исполнительный орган (ИО) выдаются сигналы управления, которые должны привести объект управления в заданное положение. Пока ЦВМ обрабатывает информацию другая порция информации в нее не вводится. И с этой точки зрения состояние ОУ в ЦВМ не наблюдаемо.
После ввода информации с чувствительных элементов (ЧЭ) в ЦВМ, она производит ее обработку, на которую уходит какое-то время. После чего на исполнительный орган (ИО) выдаются сигналы управления, которые должны привести объект управления в заданное положение. Пока ЦВМ обрабатывает информацию другая порция информации в нее не вводится. И с этой точки зрения состояние ОУ в ЦВМ не наблюдаемо.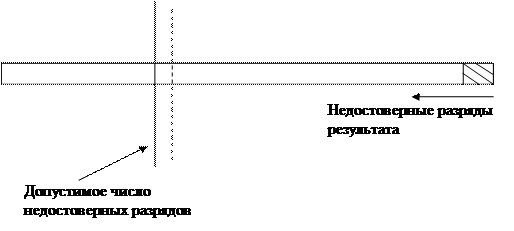 В длинной цепочке последовательных операций (формульный счет) эта погрешность постепенно растет.
В длинной цепочке последовательных операций (формульный счет) эта погрешность постепенно растет.


